統合的平等と統合的不平等

参考文献:

• ステーション B - 大学院数学 - 積分不等式 (すべての手法が要約されています)
• Zhang Yu 基礎と強化とワークブック

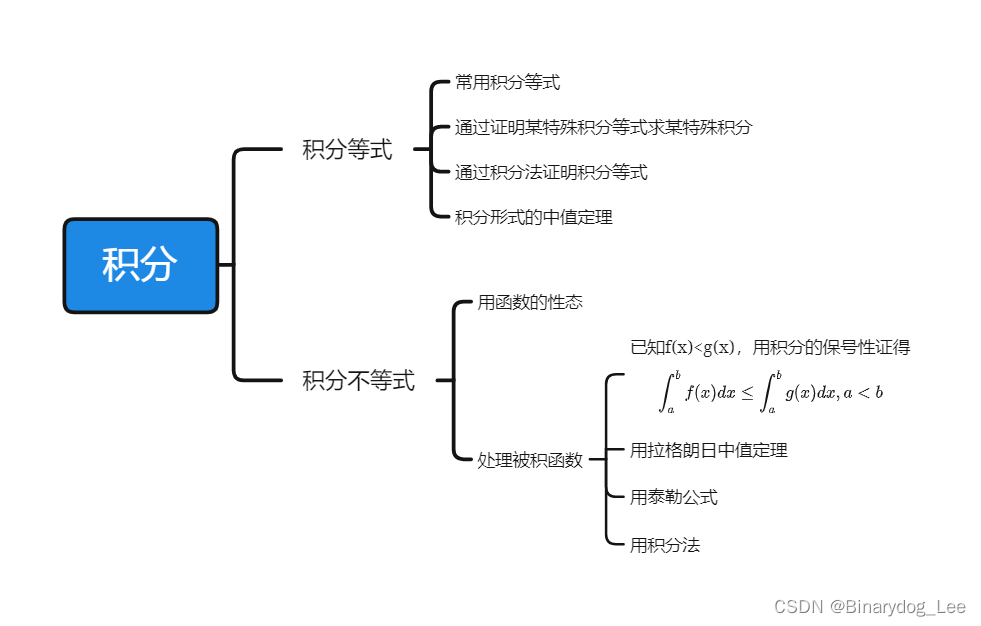
積分方程式

• 平均値定理
• 挟み込み基準
• 積分法

---

このトピックでは、次のような経験について説明します。

• f ( x ) f(x)に遭遇$f\left(x\right)$は連続なので、変数極限積分${\int }_{ある}^{}f\left(t\right)dt$の導関数は$f\left(x\right)$
• 定積分の被積分関数に可変極限積分が含まれる（または含まれる）場合は、部分積分の方法を検討してください。
• 定積分（上下限は変数ではない）は数値なので微分は0（区間内に積分が存在することは数値であり、場合によってはAに設定できる）
• NL 反転公式: $f\left(x\right)-f\left(a\right)={\int }_{ある}^{}{f}^{\text{'}}\left(x\right)dx$

$${\int }_0^{\frac{}{2}}f\left(罪x\right)dx={\int }_0^{\frac{}{2}}f\left(\cos x\right)dx$$

$${\int }_0^{}xf\left(罪x\right)dx=\frac{}{2}{\int }_0^{}f\left(罪x\right)dx$$

平均値定理

挟み込み基準

まず被積分関数をスケーリングし、次にスケーリングされた不等式全体を積分して結果を取得します。

積分法

積分不等式

関数的動作 (単調性)

f ( x ) > af(x)>aを証明するため$f\left(x\right)>a$なので、 F ( x ) = f ( x ) − a > 0 F(x)=f(x)-a>0 であることが証明できます。$F(\times )=f\left(x\right)-ある>0$。これは、$F\left(x\right)$は常に正であるか、間隔がゼロで単調増加するか、間隔の最小値が 0 より大きいか

条件$f(x)$在$[、\_b]$の連続条件の場合、通常、特定の積分限界 (通常は上限) を変更し、転置して補助関数$F\left(x\right)$ 、 F ( x ) F(x)に基づく$F\left(x\right)$の単調性は

在$[、\_b]$連続この方法の使用を判断するのも特徴です。

最後に$F^{\text{'}}(x)\; は$、 F ' ( x ) = ∫ abf ( x ) dx + cf ( x ) F'(x)=\int_a^bf(x)dx+cf(x) という形式になります。$F^{}\left({}^{\times }\right)\_={\int }_{ある}^{}f\left(x\right)dx+cf\left(x\right)$は、このとき積分の平均値定理を使って積分または関数に統一する必要があります。積分 + 関数形は扱いにくいです。

ラグランジュ平均値定理

主にf ( x ) f(x)に使用されます。$f\left(x\right)$は一次導出可能であり、特定のエンドポイント値は比較的単純です (0 であっても)

テイラー式

主にf ( x ) f(x)に使用されます。$f\left(x\right)$は 2 次導出可能であり、特定のエンドポイント値は比較的単純です (0 であっても)

積分法

部分積分法を使用して後方証明し、元の関数f ( x ) f(x)になるまで高次導関数を低次導関数に変更し続けます。$f\left(x\right)$

練習の復習

ロールの定理

Zhang Yu 基礎 30 講義 T10.1

関数のプロパティの使用を明確にした後、方程式は$\exists x$ G ( x ) = 0 G(x)=0となる$G(\times )=0$が存在する場合は、元の関数$F(\times )={\int }_{ある}^{}f\left(t\right)dt{\int }_{バツ}^{}f\left(t\right)dt$、ロールの定理を使用、$F^{}\left({}^{\times }\right)\_=G\left(x\right)$、ロールの定理を使用して存在を決定します。

変数限界積分${\int }_{ある}^{}f\left(t\right)dt$の導関数は$f\left(x\right)$

300T10.4

最初に中央値定理を積分し、次にロールを積分します。

逆関数項による扱い

この例は、Zhang Yu の基礎の講義 30 ​​の T10.2 からのものです。

テストサイト:

1. 関数$f\left(x\right)$には逆関数$g\left(x\right)$、その後任意の$x\; は$定義域内にあり、$f\left(g\right(x))=\times$確立
2. 定積分の被積分関数に可変極限積分が含まれる（または含まれる）場合は、部分積分の方法を検討してください。

まず積分法を部分に分けて、関数の可変限界を積分したものを$u$，then∫$\int など\_\_=紫外線-\int vdu$，然后$du$は可変限界積分を導出し、上限（この問題の上限は逆関数）を取り除いたものと等価です。その後、再び部分的な統合が行われました (このステップは T8.5 と似ています)。

テイラー式

Zhang Yu 基本 300 の質問 T10.9

この問題は${\int }_0^{}f\left(x\right)dx\ge 1$ですが、唯一の条件は$f\left(\frac{}{2}\right)=1$和$f^{「}（\times ）>0$、二次微分（高次微分）に遭遇すると、部分積分法やテイラーの公式が思い浮かびます。部品による統合の視覚的検査は機能しないため、テイラーの公式を考慮して、既知の$f\left(\frac{}{2}\right)=1$から残りの項までが 2 次導関数の深さになります。

$$f\left(x\right)=f\left(x_{}\right)+f^{\text{'}}\left(x_{}\right)(\times -{バツ}_{})+\frac{f^{「}(\xi }{2！}(\times -{バツ}_{}{)}^2$$

剰余を削除した後 (および$f\left(x_{}\right)=1$、${バツ}_{}=\frac{}{2}$）

$$f\left(x\right)>f\left(x_{}\right)+f^{\text{'}}\left(x_{}\right)(\times -{バツ}_{})$$

両側を積分すると以下のようになり、証明が完了します

$${\int }_0^{}f\left(x\right)dx>{\int }_0^{}[1+f^{\text{'}}(x_{}\left)\right(\times -\frac{}{2})]dx=1+f\left(\frac{}{2}\right){\int }_0^{}(\times -\frac{}{2})dx\_=1$$

絶対値の不等式

Zhang Yu 基本 300 の質問 T10.7

利用$f\left(x\right)=f\left(x\right)-f\left(a\right)={\int }_{ある}^{}{f}^{\text{'}}\left(x\right)dx$を取得するには:

$$|f(x)|=|{\int }_{ある}^{}{f}^{\text{'}}(x)dx|\le {\int }_{ある}^{}|f^{\text{'}}(x)|dx$$

同理$f\left(x\right)=f\left(x\right)-f\left(b\right)={\int }_b^{}{f}^{\prime }\left(x\right)dx$，则有：
$$|f(x)|=|{\int }_b^{}{f}^{\text{'}}(x)dx|\le {\int }_{バツ}^{}|f^{\text{'}}(x)|dx$$

今回は注意してくださいxxx < b x<b$であるため、\; x\; は$積分の下限にあります。$バツ<b$、$|f^{\text{'}}(x)|\ge 0$の場合、$b$が下限であると、負の積分になります。

2 つの式を組み合わせると、$2|f\left(x\right)|\le {\int }_{ある}^{}|f^{\text{'}}\left(x\right)|dx+{\int }_{バツ}^{}|f^{\text{'}}\left(x\right)|dx$は

定数はAに設定されます

300T10.2

$f\left(x\right)=\frac{}{1+{cos}^2バツ}+{\int }_{-p\_}^{}f\left(x\right)罪xdx$求$f\left(x\right)$，思路是任$あ={\int }_{-p\_}^{}f\left(x\right)罪xdx$，则有$f\left(x\right)=\frac{}{1+{cos}^2バツ}+次に$f ( x ) sin ⁡ x = g ( x , A ) sinxf(x)\sin x = g(x,A)sinx$f\left(x\right)罪バツ=g(x,A)をxに入れ$て積分を計算し、被積分関数のパリティを使用して 1 つの項目を削除し、$あ=\frac{{円周率}^{}}{2}$、元の$あ={\int }_{-p\_}^{}f\left(x\right)罪xdx$缶

してはいけません。

$${\int }_{-p\_}^{}f\left(x\right)罪xdx=あ={\int }_{-p\_}^{}\frac{バツ罪}{1+{\mathrm{コス}}^2バツ}$$

f ( x ) = x 1 + cos ⁡ 2 xf(x)=\frac{x}{1+\cos^2x} を考えてみましょう。$f\left(x\right)=\frac{}{1+{cos}^2バツ}$