red neuronal convolucional
Cada núcleo de convolución extrae características diferentes . Cada núcleo de convolución convoluciona la entrada para generar un mapa de características. Este mapa de características refleja las características extraídas por el núcleo de convolución de la entrada. Diferentes mapas de características muestran diferentes características en la imagen.
- Extracción de núcleo de convolución superficial: características de píxeles subyacentes, como bordes, colores y parches;
- Extracción del núcleo de convolución de nivel medio: características de textura de nivel medio como rayas, líneas, formas, etc.;
- Extracción de núcleo de convolución de alto nivel: características semánticas de alto nivel como ojos, neumáticos, texto, etc.
Finalmente, la capa de salida de clasificación genera el resultado de clasificación más abstracto.
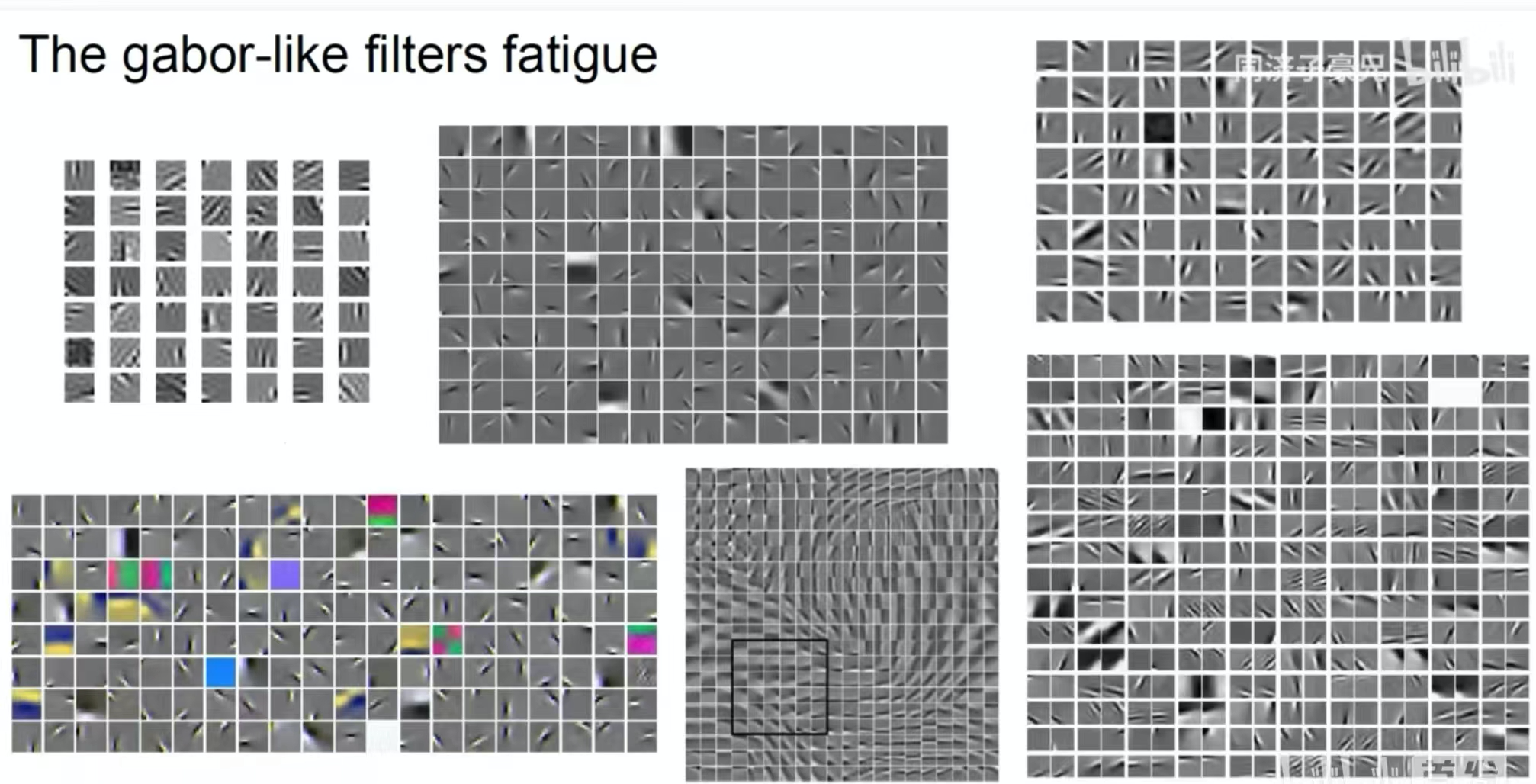
La imagen de arriba muestra las características extraídas por un núcleo de convolución poco profundo. Podemos ver que algunos núcleos de convolución extraen formas y otros extraen colores. Es una característica de convolución similar al filtro Gabor.

La imagen de arriba muestra las características extraídas por los núcleos de convolución medio y profundo. El núcleo de convolución medio extrae bloques más grandes de color y textura. Las características extraídas por el núcleo de convolución profundo pueden incluir humanos o algunas cosas concretas.
Interpretabilidad CAM
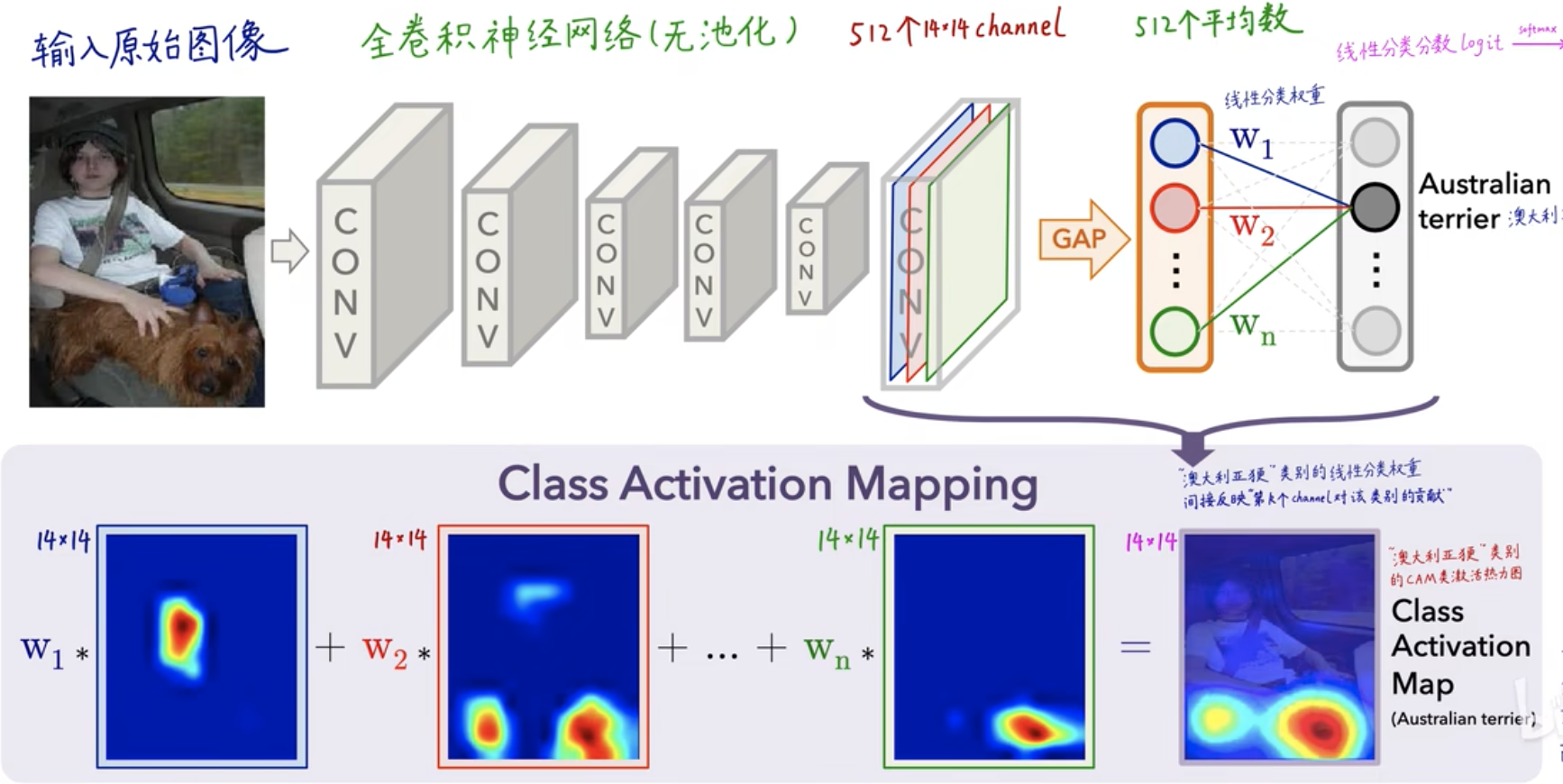
En la figura anterior, la imagen original de entrada se ha convolucionado capa por capa. En la última capa, habrá 512 núcleos de convolución y 512 canales, es decir, se han extraído 512 características profundas . Después de GAP (agrupación promedio global). Se calcula un promedio para cada característica del canal, y luego el peso (coeficiente) de cada valor de característica se obtiene a través de la capa FC (capa completamente conectada) - \(W_1, W_2, W_3,..., W_n\) , para cada categoría Puede obtener un valor de puntuación (puntuación), que se obtiene mediante
\(puntuación=W_1*valor propio azul+W_2*valor propio rojo+...+W_n*valor propio verde\)
Se obtiene y finalmente se calcula un valor de probabilidad a través de softmax, que es un proceso de clasificación CNN para el mapa de calor CAM, que se refleja principalmente en \(W_1, W_2, W_3,..., W_n\)el peso del valor de la característica .
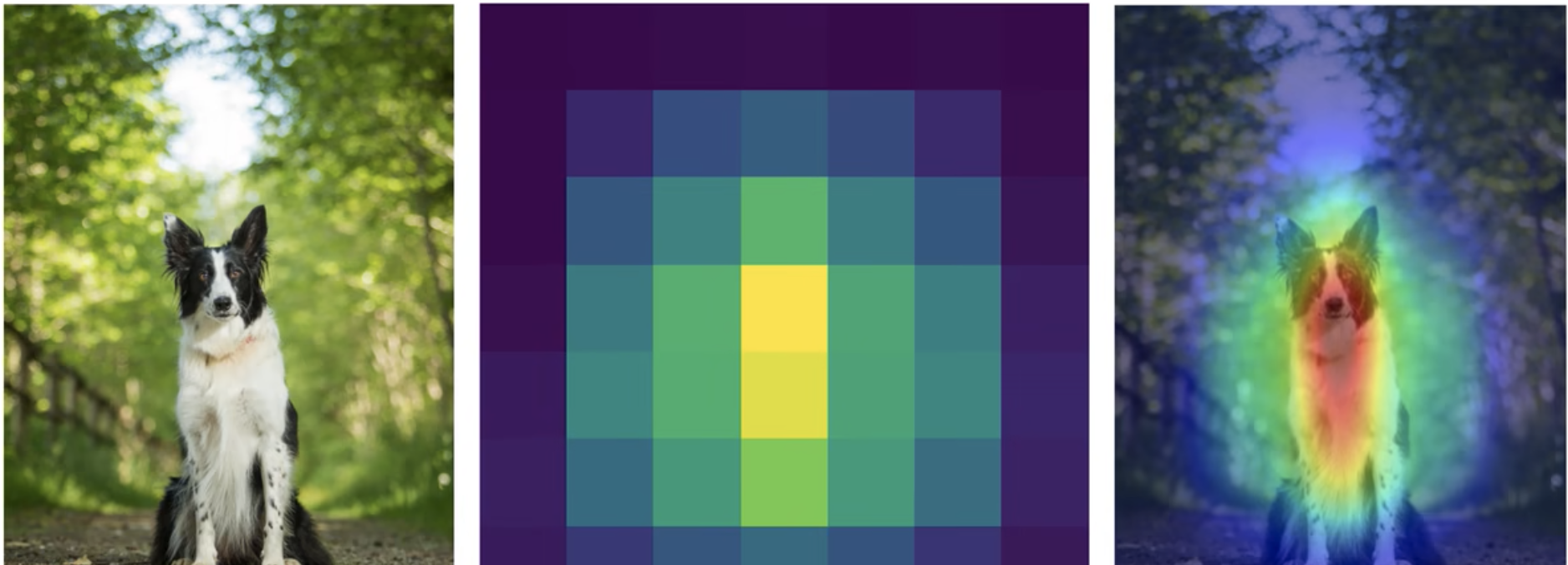
- Desventajas de la CAM
- Debe haber una capa GAP; de lo contrario, la estructura del modelo debe modificarse y volverse a entrenar.
- Solo se puede analizar la salida de la última capa convolucional y no se puede analizar la capa intermedia.
- Solo tareas de clasificación de imágenes
GradCAM

En GradCAM, en lugar de usar la capa GAP, puede usar completamente la capa FC para generar la partitura a través de la capa completamente conectada, representada por \(y^c\) .
- Derivada de una matriz
1. La derivada de una función escalar con respecto a un vector:
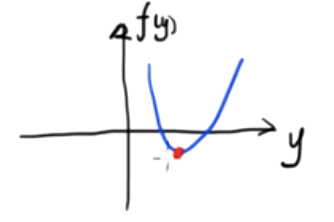
Esta es una función escalar bidimensional. Sabemos que el valor mínimo de esta función es.
\({df(y)\sobre dy}=0\)
Si esta función es una función escalar tridimensional compuesta por dos variables independientes, la imagen es la siguiente
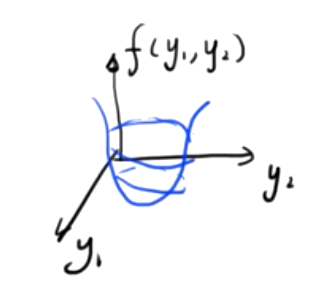
Encuentre el valor mínimo de esta función binaria, simultáneamente
- \({∂f(y_1,y_2)\sobre ∂y_1}=0\)
- \({∂f(y_1,y_2)\sobre ∂y_2}=0\)
Si una función escalar tiene n variables independientes \(f(y_1,y_2,y_3,...,y_n)\) , definimos un vector
Y=[![]() ]
]
Entonces la derivada parcial de la función con respecto al vector Y se puede definir como
\({∂f(Y)\sobre ∂Y}=\) \([\) 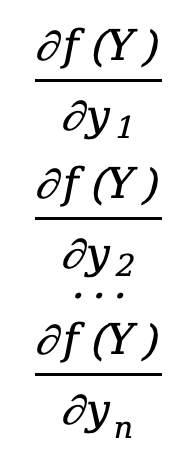 \(]\)
\(]\)
Este es un vector de columnas n * 1 y encontramos que su número de filas es el mismo que el denominador Y. Este diseño se llama diseño de denominador .
De manera similar, también podemos definir la derivada parcial de la función con respecto al vector Y como
\({∂f(Y)\sobre ∂Y}=[{∂f(Y)\sobre ∂y_1}{∂f(Y)\sobre ∂y_2}....{∂f(Y)\sobre ∂y_n }]\)
Este es un vector de filas de 1 * n, y encontramos que su número de filas es el mismo que el del numerador f (Y) (un escalar de 1 * 1) .
La disposición del denominador y la disposición del numerador son transpuestas entre sí .
Ejemplo 1: \(f(y_1,y_2)=y_1^2+y_2^2\)
Diseño del denominador:
Sea Y=[ ![]() ]
]
pero
\({∂f(Y)\sobre ∂Y}=\) [ ![]() ]=[
]=[ ![]() ]
]
Diseño molecular:
令\(Y=[y_1 y_2]\)
pero
\({∂f(Y)\sobre ∂Y}=[{∂f(Y)\sobre ∂y_1} {∂f(Y)\sobre ∂y_2}]=[2y_1 2y_2]\)
2. Derivada de la función vectorial con respecto al vector
Si nuestra función también es un vector
F(Y)=[ 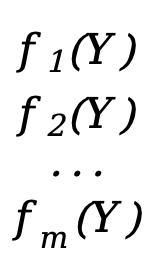 ]
]
Cada \(f_x(Y)\) (x=1,2,3,...,m) aquí es equivalente a una función escalar f(Y) anterior (la variable independiente es el vector Y), F(Y ) es una función vectorial de m*1.
Ejemplo uno:
- Y=[
 ]
] - F(Y)=[
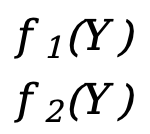 ]=[
]=[ 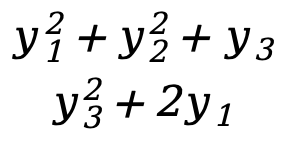 ]
]
La derivada parcial de una función vectorial con respecto a un vector, el diseño del denominador es
\({∂F(Y)\sobre ∂Y}=\) [ 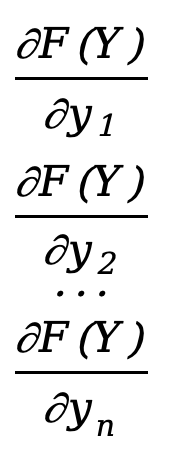 ]=[
]=[ 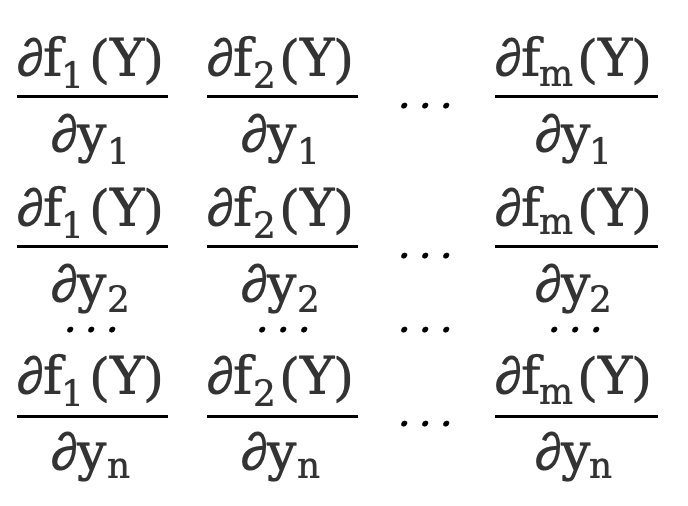 ]
]
Como en el ejemplo 1, hay
\({∂F(Y)\sobre ∂Y}=\) [ ![]() ]=[
]=[ 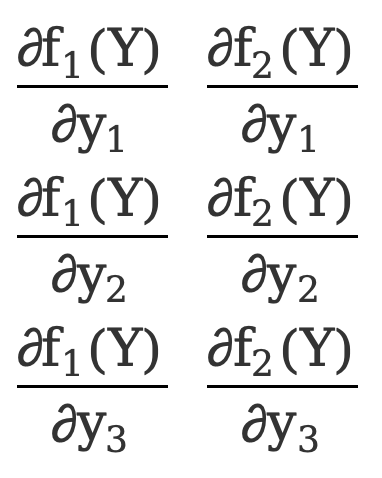 ]=[
]=[ 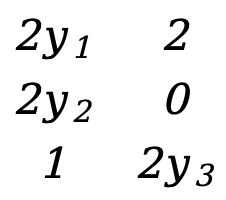 ]
]
Esta es una matriz de 3*2.
Un programador nacido en los años 90 desarrolló un software de portabilidad de vídeo y ganó más de 7 millones en menos de un año. ¡El final fue muy duro! Google confirmó despidos, relacionados con la "maldición de 35 años" de los codificadores chinos en los equipos Python Flutter Arc Browser para Windows 1.0 en 3 meses oficialmente GA La participación de mercado de Windows 10 alcanza el 70%, Windows 11 GitHub continúa disminuyendo. GitHub lanza la herramienta de desarrollo nativo de IA GitHub Copilot Workspace JAVA. es la única consulta de tipo fuerte que puede manejar OLTP + OLAP. Este es el mejor ORM. Nos encontramos demasiado tarde.
