06 Ejercicios de modelos de ecuaciones diferenciales

1. Utilice Matlab para resolver la ecuación diferencial $y^{\prime }=-2años+2x{\_}^2+2x,\_y\left(0\right)=1$

y1 = dsolve('Dy=-2*y+2*x.^2+2*x')
y2 = dsolve('Dy=-2*y+2*x.^2+2*x','y(0)=1','x')

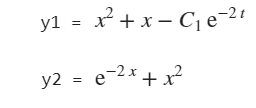
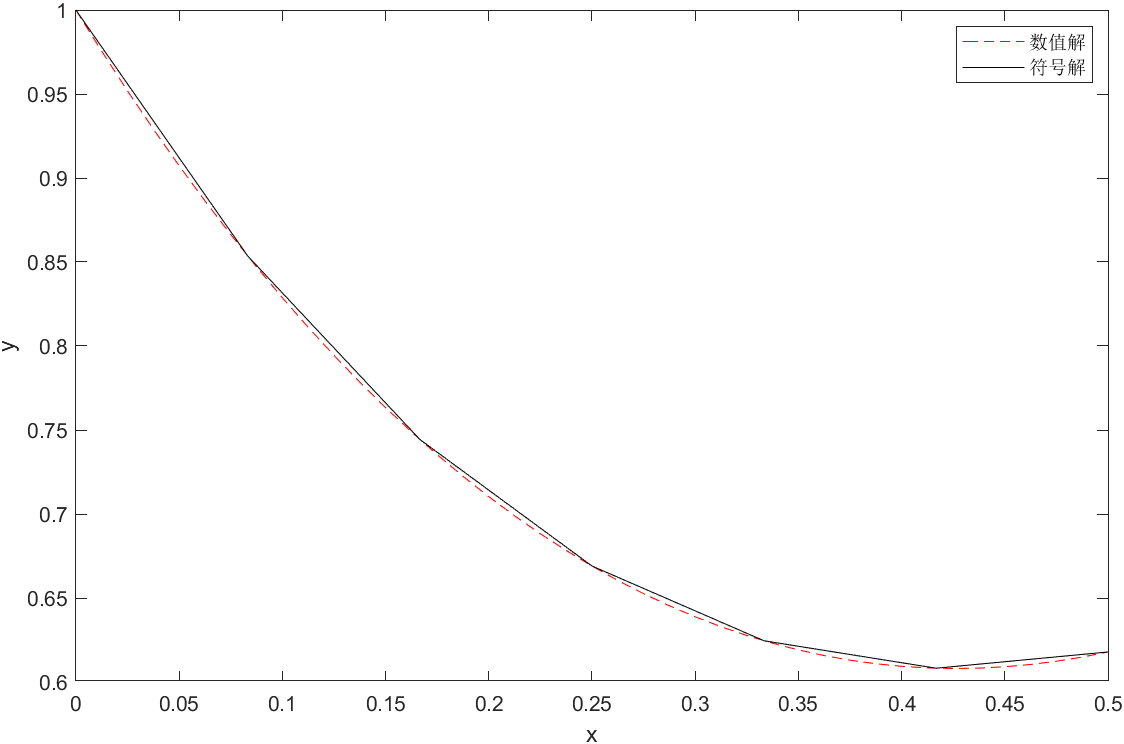
2. Usa Matlab para resolver las ecuaciones diferenciales $y^{\prime }=-2años+2x{\_}^2+2x,\_y\left(0\right)=1$ , solución simbólica y solución numérica para 0≤x≤0,5; y dibujar las curvas de solución numérica y solución simbólica en la misma interfaz gráfica.

% 使用 ode45 求解微分方程
[x, y] = ode45(@f3, [0, 0.5], 1);

yFunc = matlabFunction(y2);%将符号解转换为函数句柄
x_values = linspace(0, 0.5, 7);
y_values = yFunc(x_values);

% 绘制结果

plot(x,y,'--r')
hold on
plot(x_values,y_values,'-k')
xlabel('x');
ylabel('y');
legend('数值解','符号解')

3. Utilice Matlab para presentar la trayectoria de evolución tridimensional del sistema modelo de Lorenz y determine el impacto de dos condiciones iniciales diferentes con valores básicamente similares en la evolución de la trayectoria del sistema, analizando así la sensibilidad del modelo a la inicial. valor.

% Lorenz 系统参数
sigma = 10;
rho = 28;
beta = 8/3;

% 定义 Lorenz 系统的微分方程
dxdt = @(t, x) [sigma * (x(2) - x(1));
                x(1) * (rho - x(3)) - x(2);
                x(1) * x(2) - beta * x(3)];

% 模拟 Lorenz 系统演化
[t1, y1] = ode45(dxdt, [0, 100], [1; 0; 0]);
[t2, y2] = ode45(dxdt, [0, 100], [1.001; 0; 0]);

% 绘制三维演化轨迹
figure;
subplot(2,2,1);
plot3(y1(:, 1), y1(:, 2), y1(:, 3), 'b', 'LineWidth', 1.5);
hold on;
plot3(y2(:, 1), y2(:, 2), y2(:, 3), 'r', 'LineWidth', 1.5);
xlabel('x');
ylabel('y');
zlabel('z');
title('Lorenz 系统三维演化轨迹');
legend('初始条件1', '初始条件2');
%view(-35, 15);  % 设置视角
subplot(2,2,2);
plot(t1,y1(:,1),t2,y2(:,1))
title('X(1)');
subplot(2,2,3);
plot(t1,y1(:,2),t2,y2(:,2))
title('X(2)');
subplot(2,2,4);
plot(t1,y1(:,3),t2,y2(:,3))
title('X(3)');

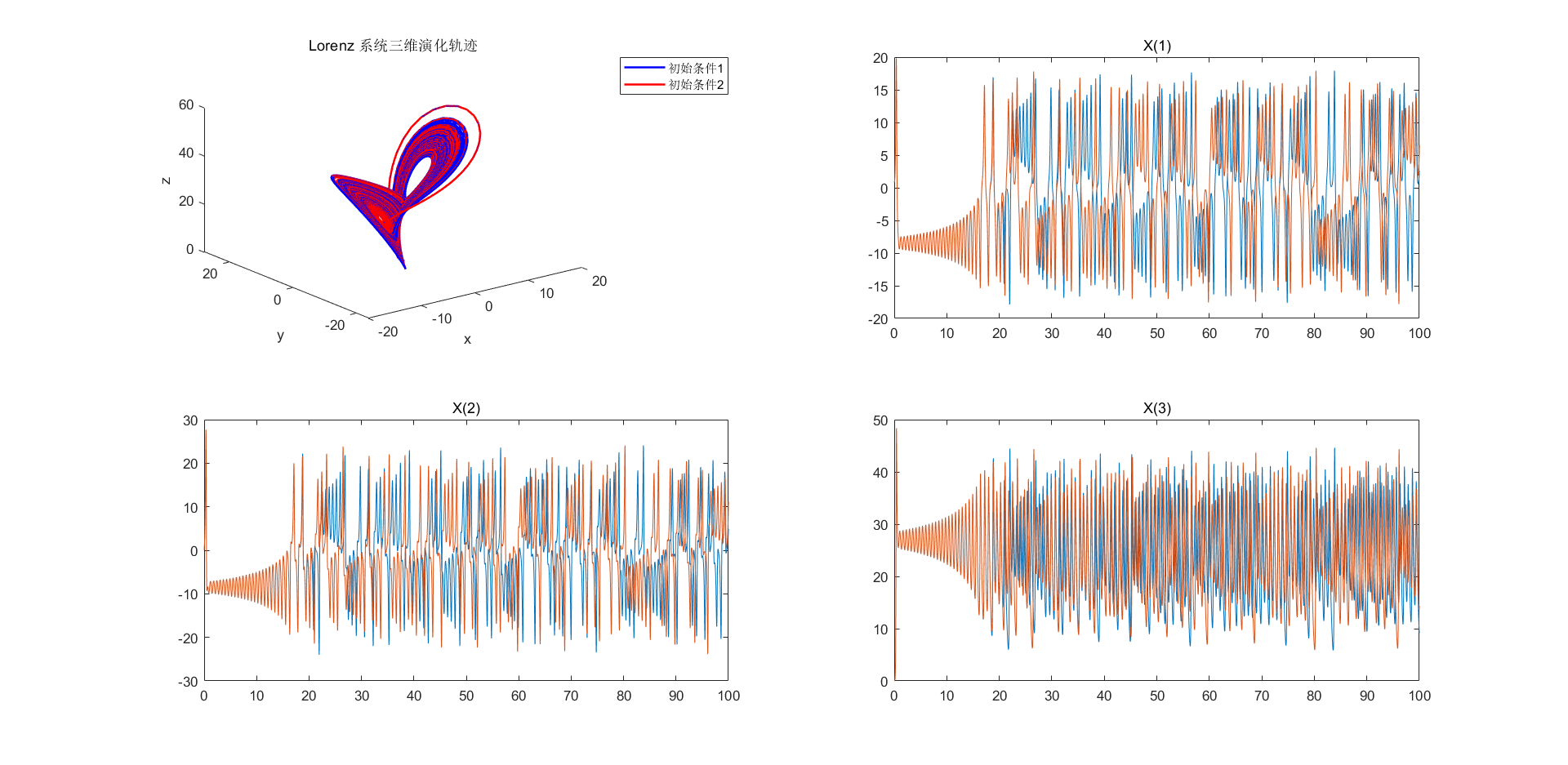
Pequeños cambios en las condiciones iniciales pueden conducir a una rápida separación de las trayectorias del sistema.

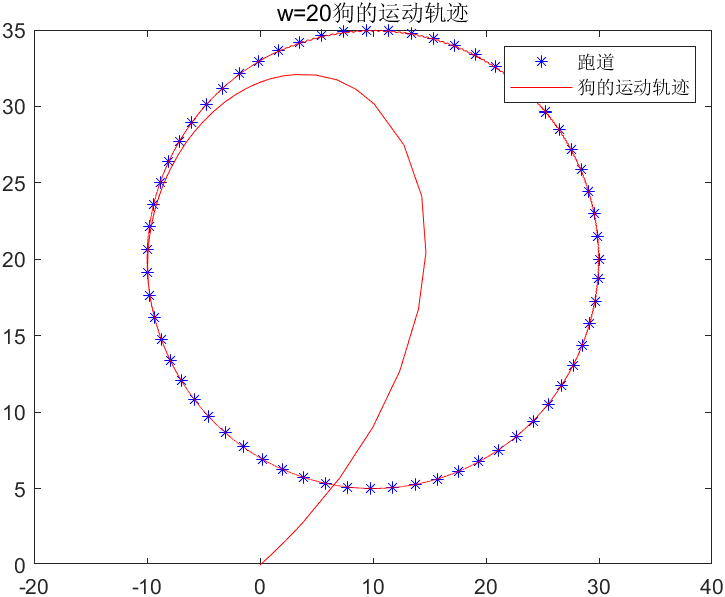
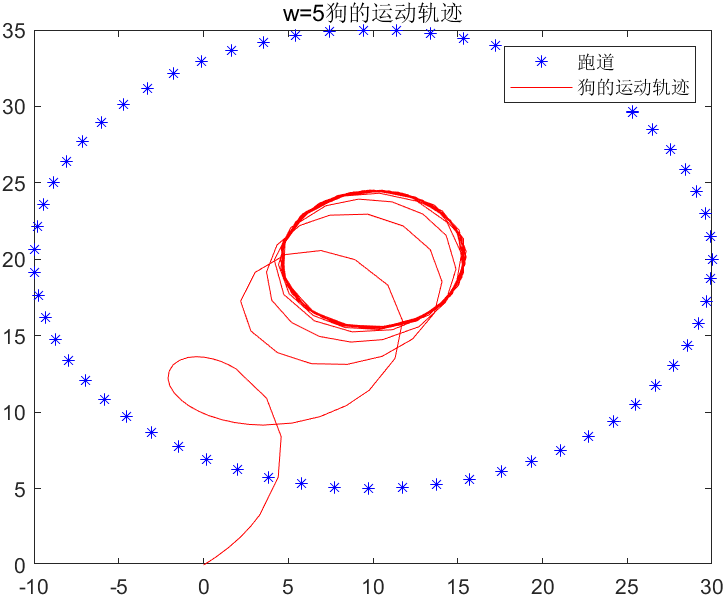
4. Un corredor corre en un avión de la siguiente manera: X=10+20costo, Y=20+15sint. De repente un perro lo ataca. El perro parte desde el origen y corre hacia el corredor a una velocidad constante w. El perro se mueve. La dirección es siempre hacia el corredor. Encuentre la trayectoria de movimiento del perro cuando w = 20 y w = 5 respectivamente.

pista:

clf;
[t1,y1] = ode45('f4',[0,10],[0;0]);
T = 0:0.1:2*pi;
X = 10 + 20 * cos(T);
Y = 20 + 15 * sin(T);
plot(X,Y,'b*',y1(:,1),y1(:,2),'r')
title('w=20狗的运动轨迹');
legend('跑道', '狗的运动轨迹');
[t2,y2] = ode45('f5',[0,100],[0;0]);
plot(X,Y,'b*',y2(:,1),y2(:,2),'r')
title('w=5狗的运动轨迹');
legend('跑道', '狗的运动轨迹');

function dy = f4(t,y)
dy = zeros(2,1);
dy(1) = 20 * (10 + 20 * cos(t) - y(1)) / sqrt((10 + 20 * cos(t) - y(1))^2 + (20 + 15 * sin(t) - y(2))^2);
dy(2) = 20 * (20 + 15 * sin(t) - y(2)) / sqrt((10 + 20 * cos(t) - y(1))^2 + (20 + 15 * sin(t) - y(2))^2);

end

function dy = f5(t,y)
dy = zeros(2,1);
dy(1) = 5 * (10 + 20 * cos(t) - y(1)) / sqrt((10 + 20 * cos(t) - y(1))^2 + (20 + 15 * sin(t) - y(2))^2);
dy(2) = 5 * (20 + 15 * sin(t) - y(2)) / sqrt((10 + 20 * cos(t) - y(1))^2 + (20 + 15 * sin(t) - y(2))^2);

end