Aprendizaje profundo para resolver ecuaciones diferenciales Serie cinco: PINN Resuelva los problemas directos e inversos de la ecuación de Navier-Stokes

A continuación, presentaré la red neuronal de conocimiento de física integrada (PINN) para resolver ecuaciones diferenciales. En primer lugar, se introduce el método básico de PINN y, basándose en el marco de solución de PINN de Pytorch, se resuelve la ecuación bidimensional de Navier-Stokes con término de tiempo.

Red neuronal integrada de conocimiento físico (PINN) Introducción y documentos relacionados
Aprendizaje profundo para resolver ecuaciones diferenciales Serie 1: Marco de solución de PINN (Poisson 1d)
Aprendizaje profundo para resolver ecuaciones diferenciales Serie 2: PINN para resolver problemas de reenvío de ecuaciones de hamburguesa
Aprendizaje profundo para resolver ecuaciones diferenciales Serie 3: PINN resuelve el problema inverso de la ecuación de la hamburguesa
Deep learning para resolver la ecuación diferencial serie IV: Basado en la función de activación adaptativa PINN resuelve el problema inverso de la ecuación de la hamburguesa Deep learning
para resolver la ecuación diferencial serie V: PINN resuelve el problema directo e inverso de la ecuación de Navier-Stokes

1. Introducción a PINN

Como una poderosa herramienta de procesamiento de información, la red neuronal se ha utilizado ampliamente en los campos de la visión por computadora, la biomedicina y la ingeniería de petróleo y gas, lo que ha desencadenado cambios tecnológicos en muchos campos. La red de aprendizaje profundo tiene una capacidad de aprendizaje muy fuerte, no solo puede descubrir leyes físicas, sino también resolver ecuaciones diferenciales parciales. En los últimos años, la solución de ecuaciones diferenciales parciales basadas en el aprendizaje profundo se ha convertido en un nuevo foco de investigación. La red neuronal informada por la física integrada (PINN) es una aplicación de máquinas científicas en el dominio numérico tradicional, que se puede utilizar para resolver varios problemas relacionados con ecuaciones diferenciales parciales (PDE), incluida la resolución de ecuaciones, inversión de parámetros, descubrimiento de modelos, control y optimizacion etc

2. Método PINN

La idea principal de PINN se muestra en la Figura 1, primero construya un resultado de salida como $tu$La red neuronal de ^, que se usa como un modelo proxy para la solución PDE, y la información PDE se usa como una restricción, codificada en la función de pérdida de la red neuronal para el entrenamiento$\stackrel{.}{}$La función de pérdida incluye principalmente cuatro partes: pérdida de estructura diferencial parcial (pérdida PDE), pérdida de condición de valor límite (pérdida BC), pérdida de condición de valor inicial (pérdida IC) y pérdida de condición de datos reales (pérdida de datos).

Figura 1: Diagrama esquemático de PINN

En particular, considere el siguiente problema PDE, donde la solución de la PDE $u\left(x\right)$在$Oh\subset R^d$ definición, donde$X=\left(X_{},\dots ,X_{}\right)$：
$$F\left(X;\frac{\partial }{\partial x_{}},\dots ,\frac{\partial }{\partial x_{}};\frac{{\partial }^2}{\partial x_{}\partial x_{}},\dots ,\frac{{\partial }^2}{\partial x_{}\partial x_{}}\right)=0,X\in \Omega$$
Al mismo tiempo, satisfaga el siguiente límite
$$B(tú,x)=0\text{ en }\partial \Omega$$

El proceso de solución de PINN incluye principalmente:

• El primer paso es definir el modelo de red neuronal de la capa totalmente conectada de la capa D:
  $${norte}_{}:=L_{}\circ pag\circ L_{re-}\circ pag\circ \cdots \circ pag\circ L_{}$$
  式中：
  $$\begin{array}{rl}{L}_{}\left(X\right)& :=W_{}X+b_{},W_{}\in R^{d_{}\times re},b_{}\in R^{d_{}}\\ L_{}\left(X\right)& :=W_{}X+b_{},W_{}\in R^{d_{}\times {re}_{yo-}},b_{}\in R^{d_{}},\forall yo=2,3,\cdots D-1,\\ L_{}(x& :=W_{}X+b_{},W_{}\in R^{N\times {re}_{re-}},b_{}\in R^{N.}\end{array}$$
  y $\sigma$ es la función de activación,$W$ y$b$ son los parámetros de peso y sesgo.
• El segundo paso, para medir la red neuronal $\widehat{tu}$和约束之间的差异，考虑损失函数定义：
  $$L\left(yo\right)=w_{}{L}_{PD}\left(yo;T_{}\right)+w_{}{L}_{yo}\left(yo;T_{}\right)+w_{}{L}_B\left(yo,;T_{}\right)+w_{}{L}_{datos\_\_}\left(yo,;T_{datos\_\_}\right)$$
  donde:
  $$\begin{array}{rl}{L}_{PD}\left(yo;T_{}\right)& =\frac{}{|T_{}|}\underset{x\in T_{}}{}{\Vert F\left(X;\frac{\partial tu}{\partial x_{}},\dots ,\frac{\partial tu}{\partial x_{}};\frac{{\partial }^{2}tu}{\partial x_{}\partial x_{}},\dots ,\frac{{\partial }^{2}tu}{\partial x_{}\partial x_{}}\right)\Vert }_2^{}\\ L_{yo}\left(yo;T_{}\right)& =\frac{}{|T_{}|}\underset{x\in T_{}}{}\Vert \widehat{tu}\left(x\right)-tu\left(x\right){\Vert }_2^{}\\ L_B\left(yo;T_{}\right)& =\frac{}{|T_{}|}\underset{x\in T_{}}{}\Vert B(\widehat{tu},X){\Vert }_2^{}\\ L_{datos\_\_}(yo;T_{datos\_\_}& =\frac{}{|T_{datos\_\_}|}\underset{x\in T_{datos\_\_}}{}\Vert \widehat{tu}\left(x\right)-tu\left(x\right){\Vert }_2^{}\end{array}$$
  $w_{}$，$w_{}$、$w_{}$y $w_{}$es el peso $T_{}$，$T_{}$、$T_{}$和$T_{datos\_\_}$Representa puntos residuales de PDE, valor inicial, valor límite y valor verdadero. Aquí $T_{}\subset \Omega$ es un conjunto predefinido de puntos para medir la salida de la red neuronal$\widehat{tu}$ Grado de coincidencia con PDE.
• Finalmente, use el algoritmo de optimización de gradiente para minimizar la función de pérdida hasta que se encuentren los parámetros de red que cumplan con la precisión de la predicción .

Vale la pena señalar que para problemas inversos, es decir, algunos parámetros en la ecuación son desconocidos. Si solo se conocen la ecuación PDE y las condiciones de contorno, y se desconocen los parámetros PDE, el problema inverso es un problema indeterminado, por lo que se debe conocer otra información, como algunos puntos de observación $el\; valor\; de\; ud$ . En este caso, el método PINN puede utilizar los parámetros de la ecuación como variables desconocidas y agregarlos al entrenador para su optimización.La función de pérdida incluye la pérdida de datos.

3. Definición de resolución de problemas: problemas directos e inversos

ut + λ 1 ( uux + vuy ) = − px + λ 2 ( uxx + uyy ) vt + λ 1 ( uvx + vvy ) = − py + λ 2 ( vxx + vyy )
$$\begin{array}{rl}& {tu}_{}+{yo}_{}\left(Uu{uu}_{}+tu{\_}_{}\right)=-{pag}_{}+{yo}_{}\left({tu}_x+{tu}_{yy}\right)\\ & v_{}+{yo}_{}\left(u{v}_{}+vv{\_}_{}\right)=-{pag}_{}+{yo}_{}(v_x+v_{yy}\end{array}$$
Problema positivo :

• parámetroλ ${yo}_{}=1$ ,${yo}_{}=0.01$ es un parámetro conocido, el problema son condiciones de contorno y ecuaciones diferenciales conocidas, y u, v, p están resueltas.
  Problema inverso:
• Sencillo ${yo}_{},{yo}_{}$Para parámetros desconocidos, el problema son condiciones de contorno conocidas y ecuaciones diferenciales, pero los parámetros en la ecuación son desconocidos, resuelva u, v, p y los parámetros de la ecuación.

Considere resolver el campo de flujo incompresible en el área rectangular que se muestra en la Figura 2. En particular, la solución de la ecuación del fluido satisface funciones libres de divergencia al mismo tiempo, que se pueden expresar como: ux + vy = 0 u_x+ v_y=
$${tu}_{}+v_{}=0$$
red, la salida debe ser tridimensional ($tu,v,p$ ), pero en el proceso de solución se puede introducir la función latente,$\psi (x,y,t)$ , cumple con los requisitos,
$$tu={pag}_{},v=-{pag}_{}$$
salida de la red, se puede expresar como una bidimensional ( $pd,pag$ )
。

Figura 2: Problema de flujo alrededor de un cilindro ​

Figura 3: Campo de flujo en un espacio bidimensional

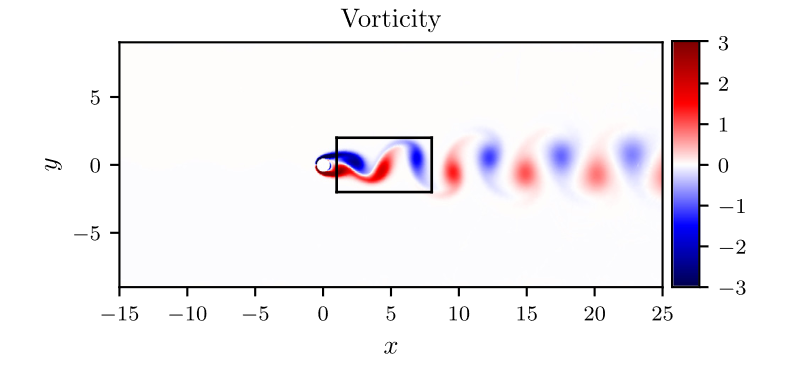
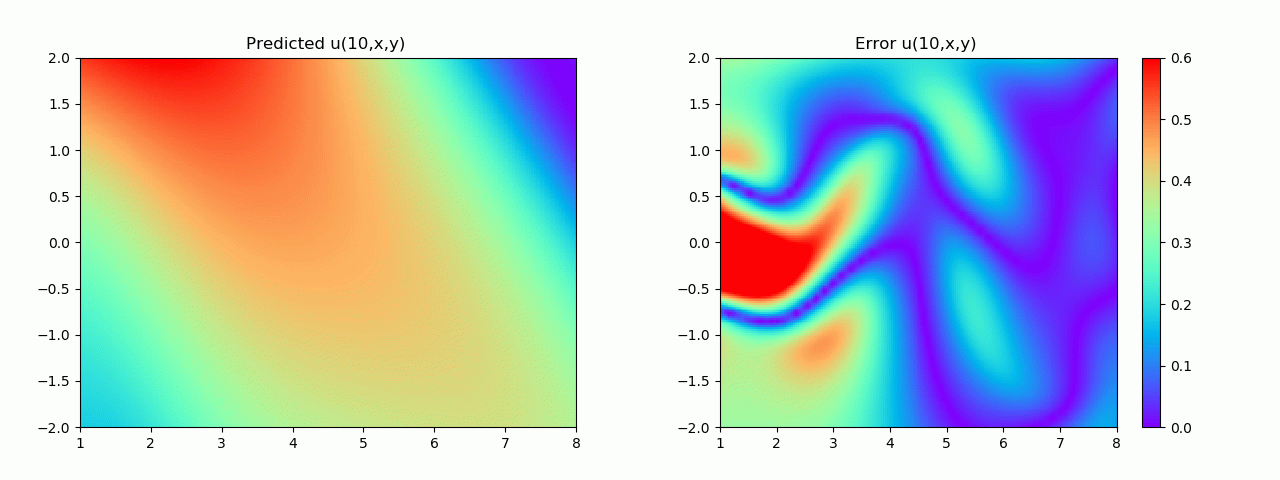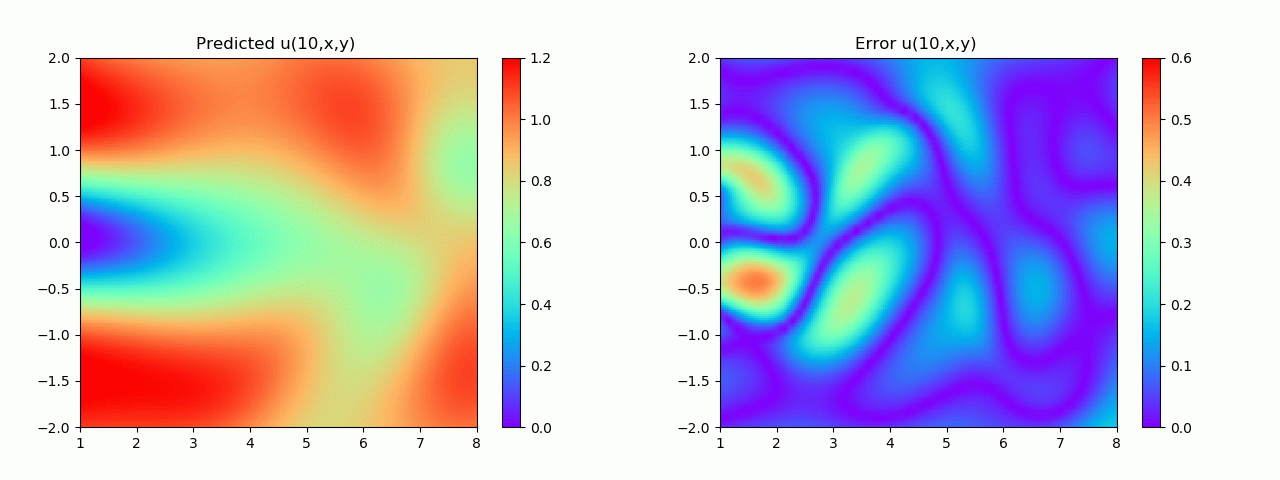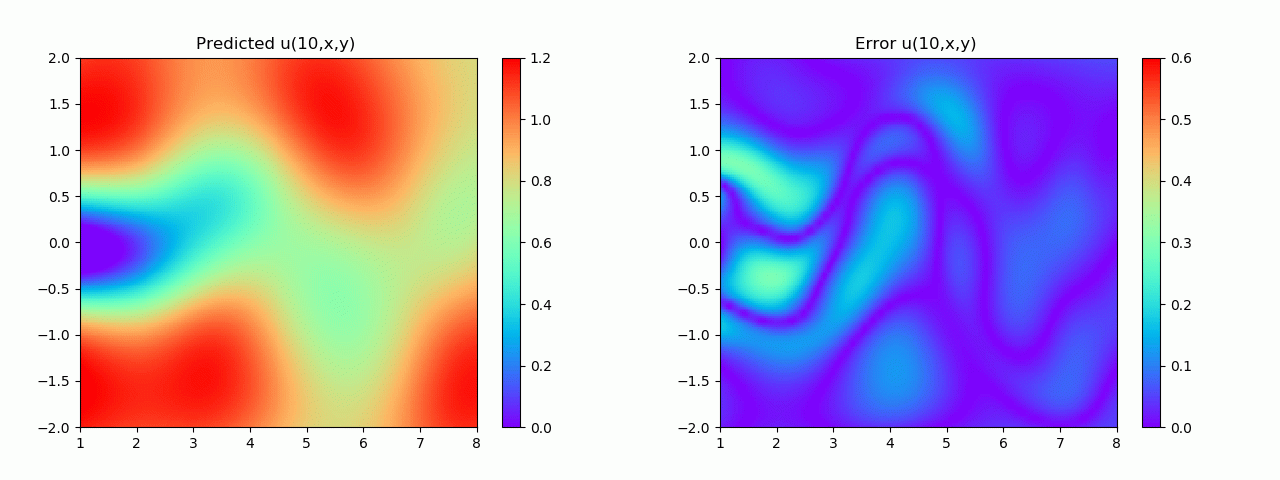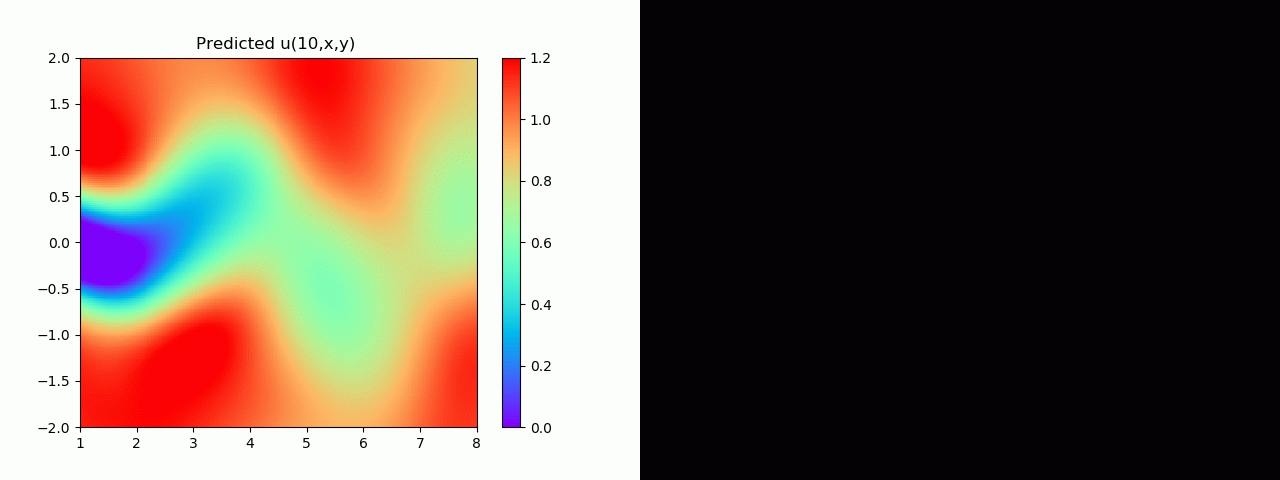
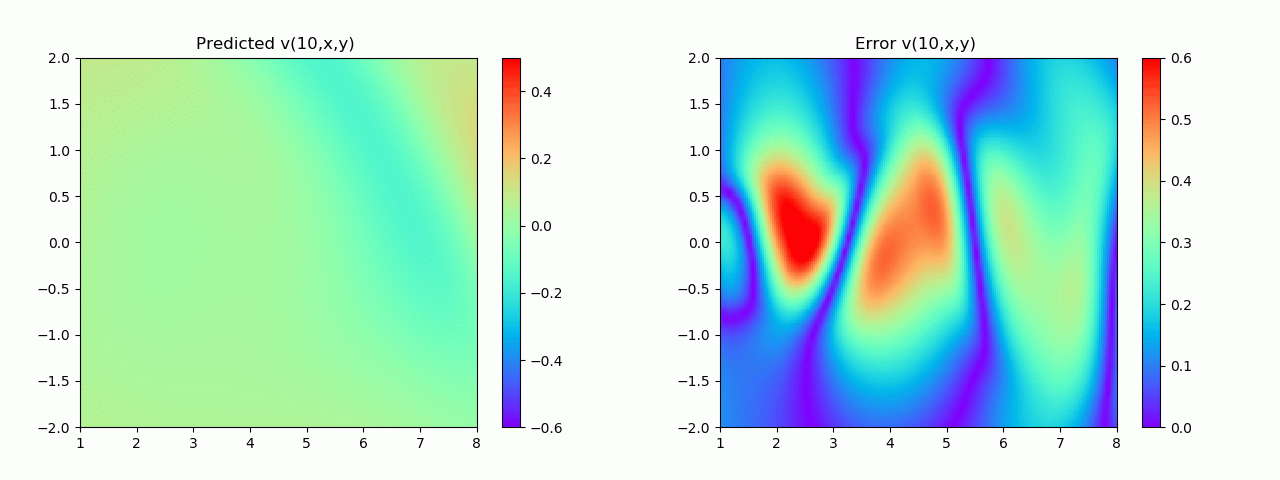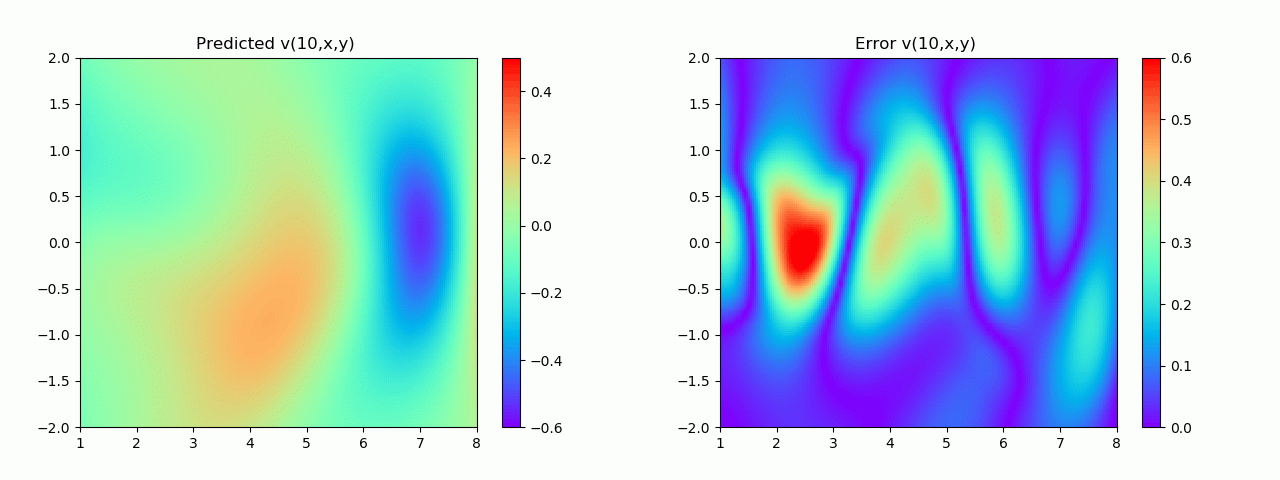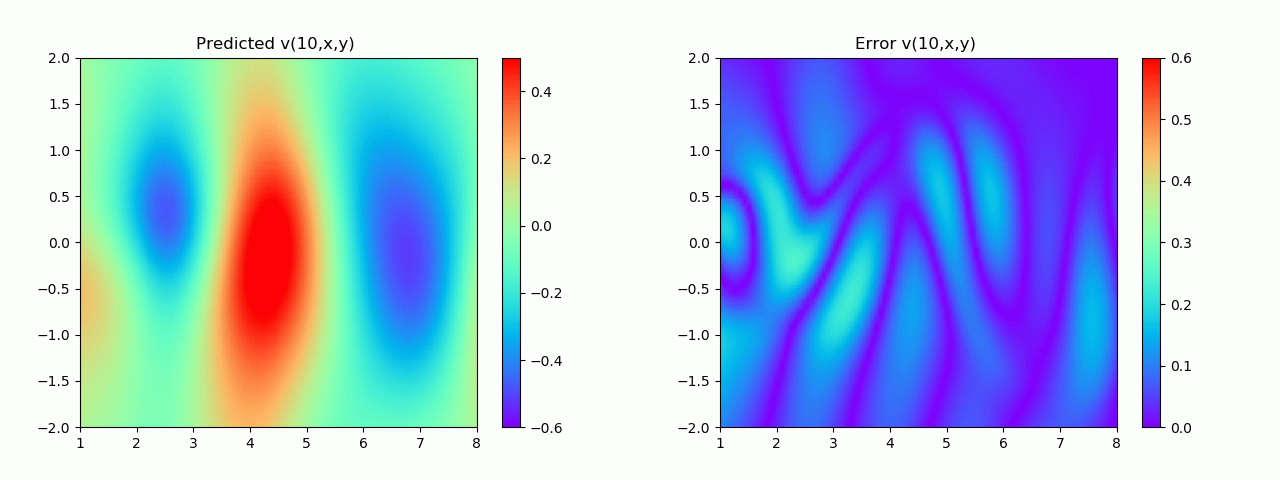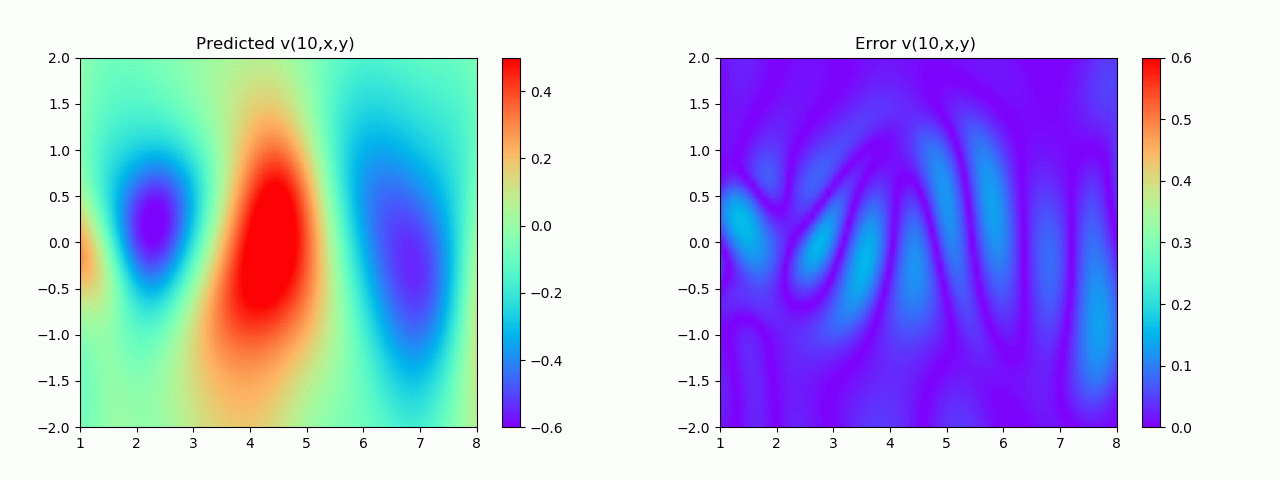
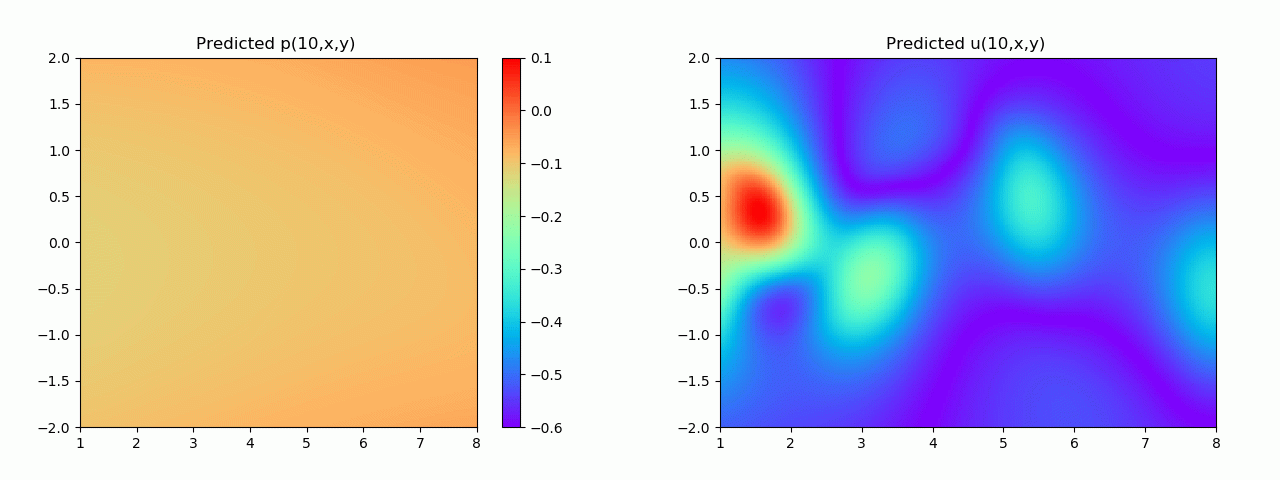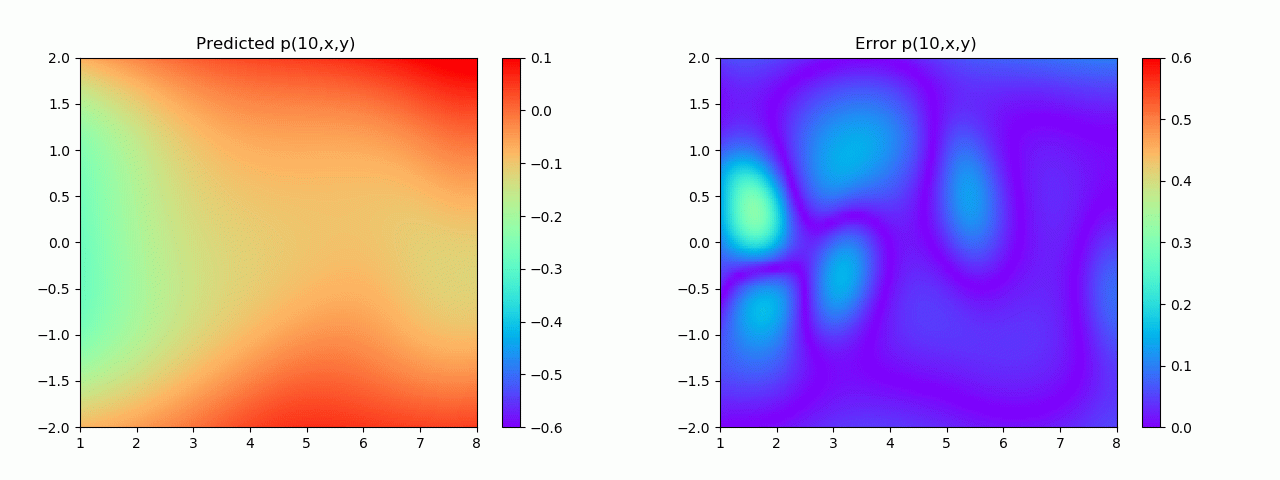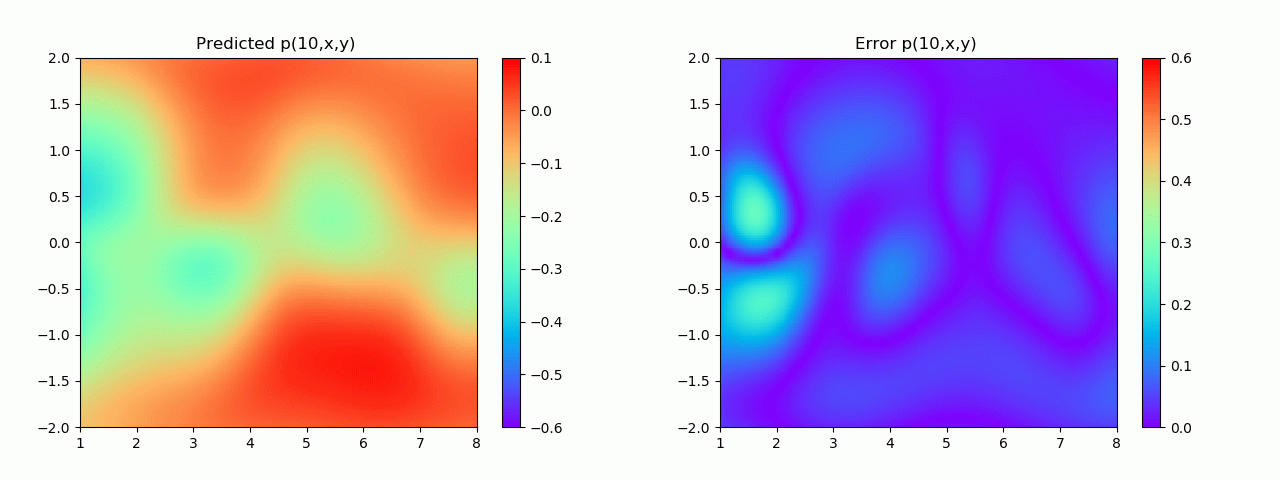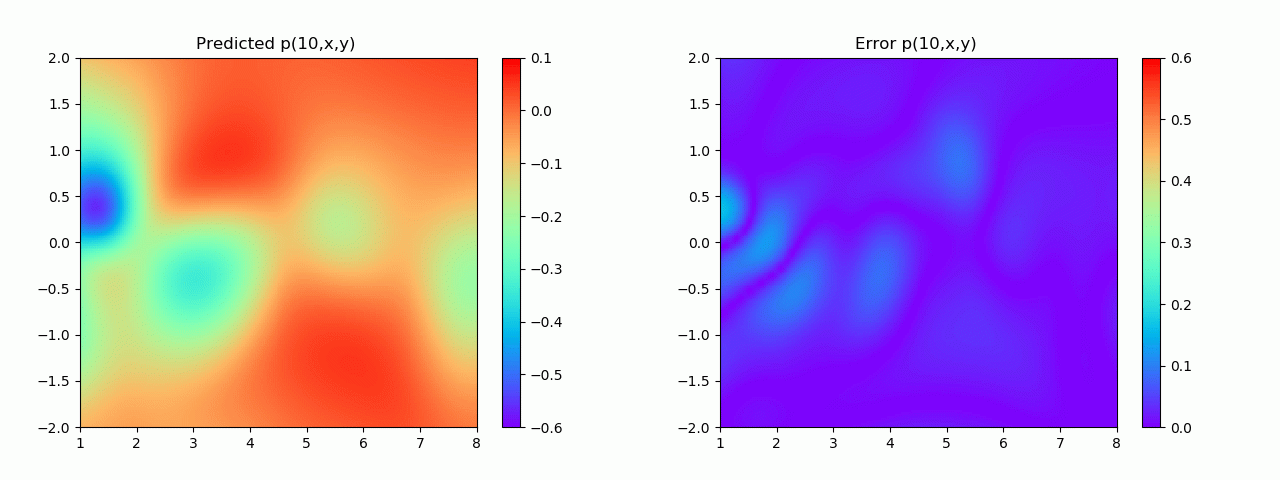
En particular, para demostrar el efecto, aquí elegimos el efecto de predicción de comparación de campo de flujo por debajo de 10 s.

Figura 4: u, v menores de 10 años

​

Figura 5: p menos de 10 s

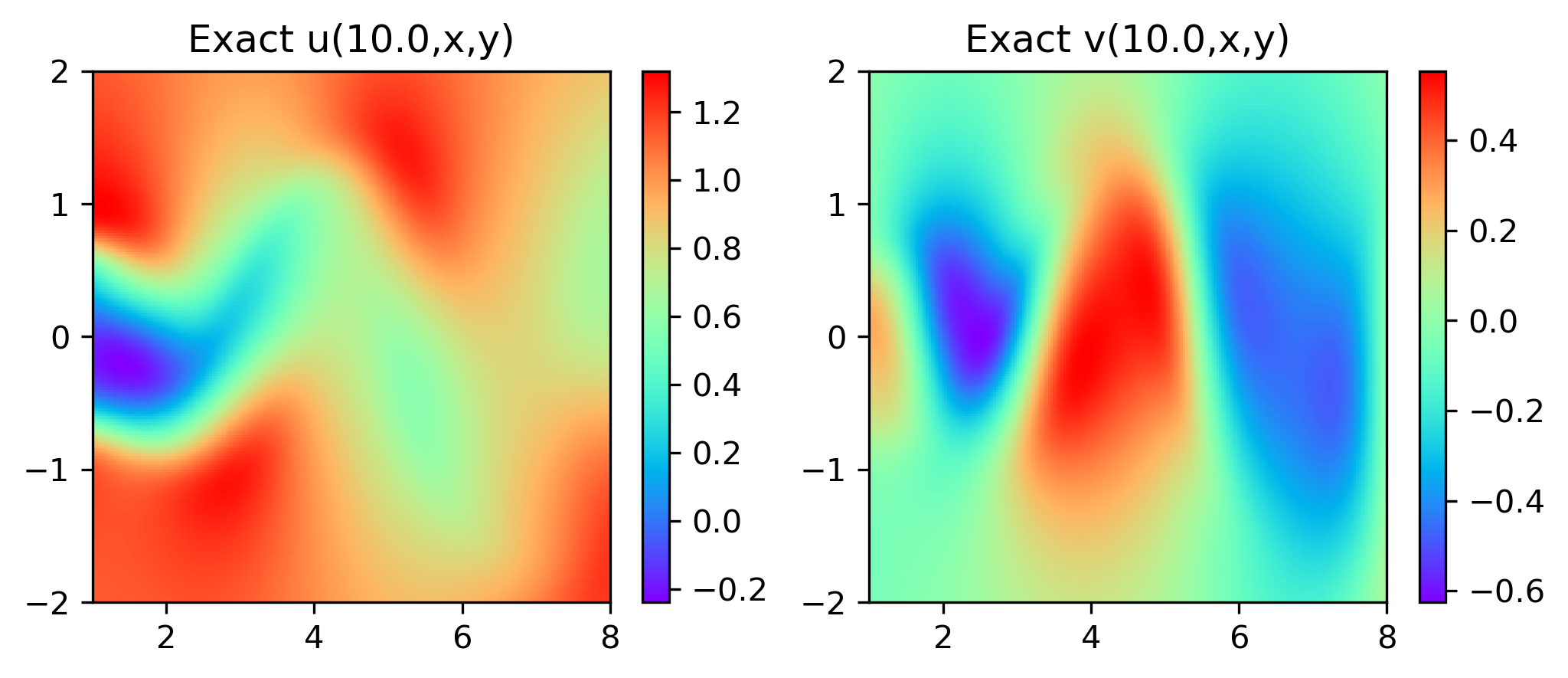
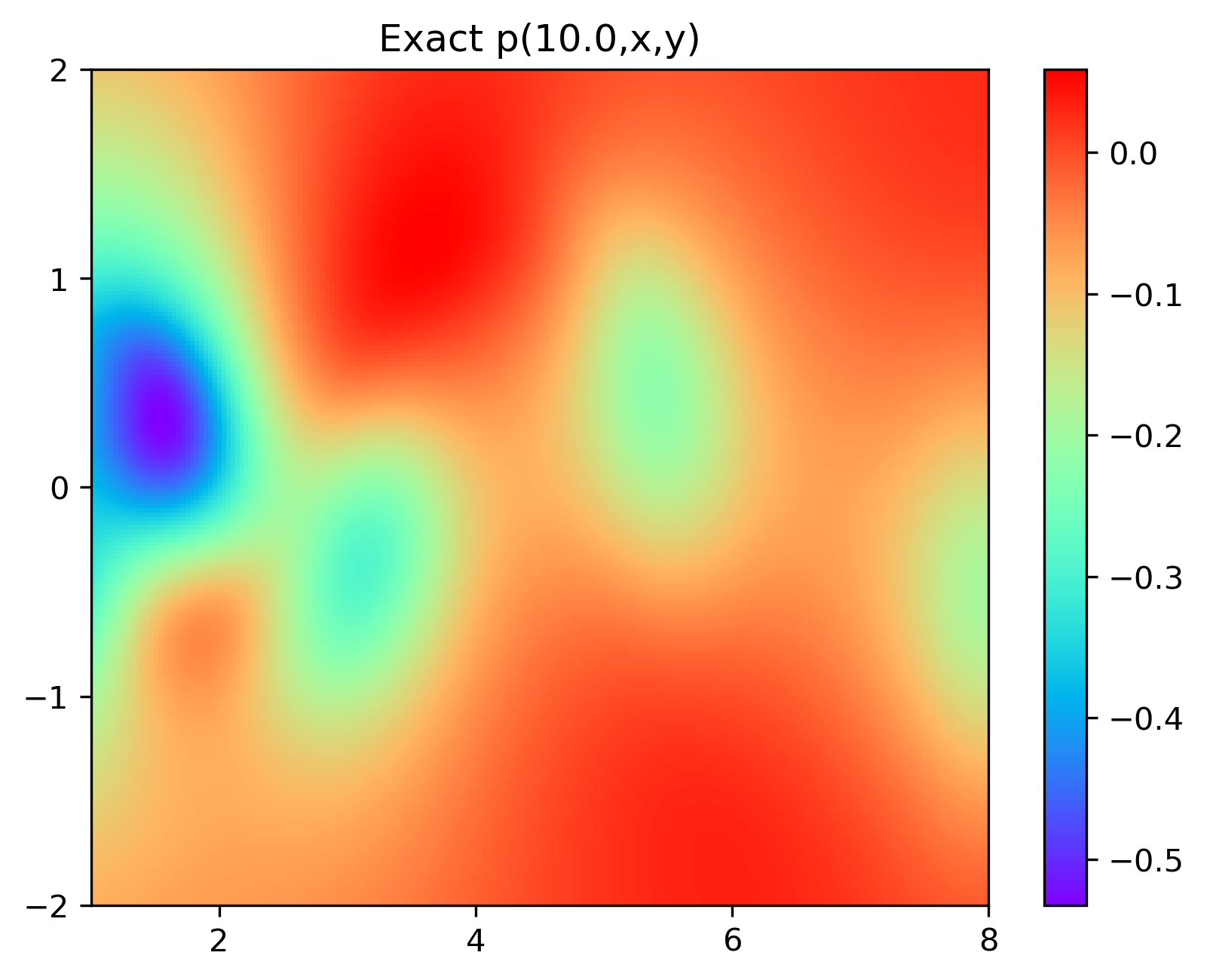
4. Visualización de resultados

4.1 Resultados experimentales del problema positivo

Los resultados experimentales se muestran en la figura 6-8 A través del entrenamiento, PINN puede lograr
una predicción

Figura 6: gráfico de u y error previsto

​

Figura 7: gráfico de v y error pronosticado

​

Figura 8: Predicción p y diagrama de error