Esta es una revisión de GNN, publicada en TNNLS en 2021. Este blog tiene como objetivo registrar algunos conceptos básicos de GNN.
Dirección del papel: papel
1. Introducción, antecedentes y definiciones
Para datos de imágenes, CNN tiene invariancia de traducción y conectividad local, por lo que puede aprender bien en el espacio euclidiano, pero para datos con estructura gráfica (como moléculas químicas de redes sociales, etc.), es necesario utilizar GNN para el aprendizaje.
La primera red GNN siguió la iteración cíclica similar a RNN (RecGNN), y el objeto principal era DAG (gráfico acíclico dirigido). La condición para detener este método es que la representación de los nodos tiende a ser estable.
Posteriormente se desarrolló la red de gráficos convolucionales (ConvGNN), basada principalmente en el dominio espectral (dominio de frecuencia) y basada en el dominio espacial, además de autocodificadores de gráficos (GAE) y GNN espacio-temporal (espacial-temporal).
Por lo tanto, este artículo divide GNN principalmente en estos cuatro tipos:
- GNN recurrente
- GNN convolucionales
- Codificador automático de gráficos
- GNN espaciotemporal
Más tarde, el autor habló principalmente sobre la diferencia entre GNN y las dos tareas:
GNN e incrustación de red.La incrustación de red tiene como objetivo codificar los nodos de una red en una representación vectorial de baja dimensión y mantener la topología de la red sin cambios, de modo que después de la reducción de dimensionalidad, algunas tareas como la clasificación y la agrupación se puedan realizar mediante métodos tradicionales. máquinas Implementación de métodos de aprendizaje (como SVM). Por lo tanto, la relación entre GNN y la incrustación de red es que GNN puede aprender una representación de baja dimensión a través de un codificador automático de gráficos, es decir, la tarea de incrustación de red. Es principalmente a través de la reducción de dimensionalidad, para lograr el propósito de aplicar métodos de aprendizaje automático.
GNN y métodos del kernel de gráficos : El método del kernel de gráficos codifica principalmente un gráfico en un espacio vectorial para aplicar tareas como SVM (nivel de gráfico).
2. Taxonomía y marco
Como se mencionó anteriormente, este documento divide GNN en cuatro categorías, como se muestra en la siguiente figura:
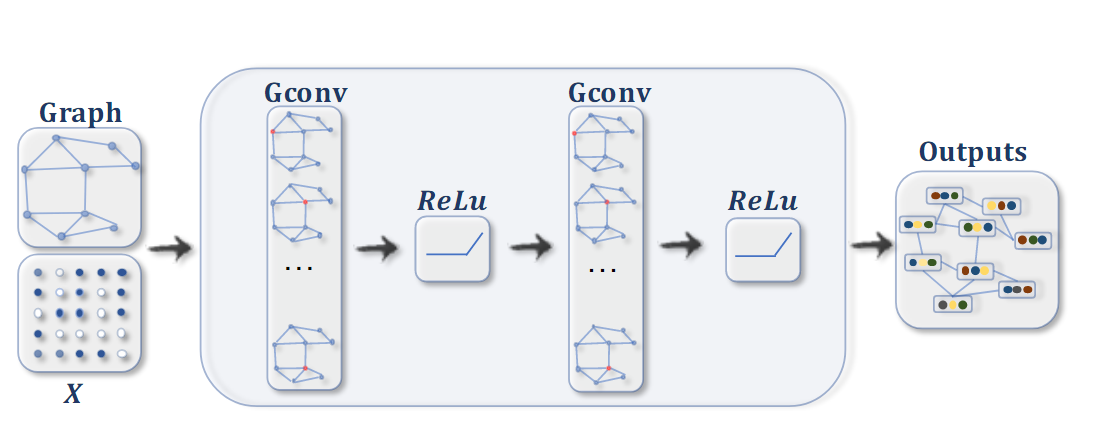
ConvGNN para tareas de clasificación de nodos . Para cada nodo, la información de sus nodos adyacentes se agrega en cada iteración (convolución de gráfico) y finalmente el nodo se clasifica mediante una transformación no lineal. Donde X ∈ R n × d X\in\ mathbb{ R}^{n\veces d}X∈Rn × d representa la matriz compuesta por características de nodos.
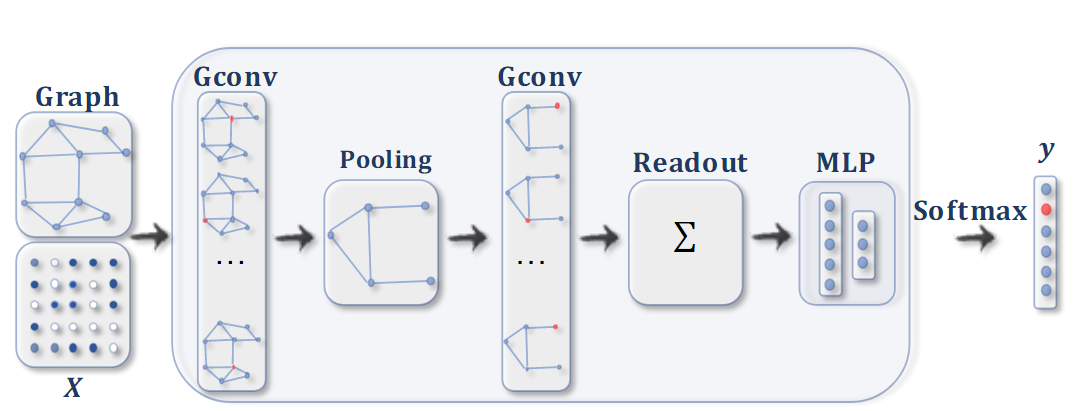
ConvGNN para tareas de clasificación de gráficos . Después de la operación de convolución del gráfico, se usa una capa de agrupación para convertir el gráfico en un subgrafo para obtener representaciones más altas del gráfico. Finalmente, se usa una función de lectura para clasificar el gráfico.
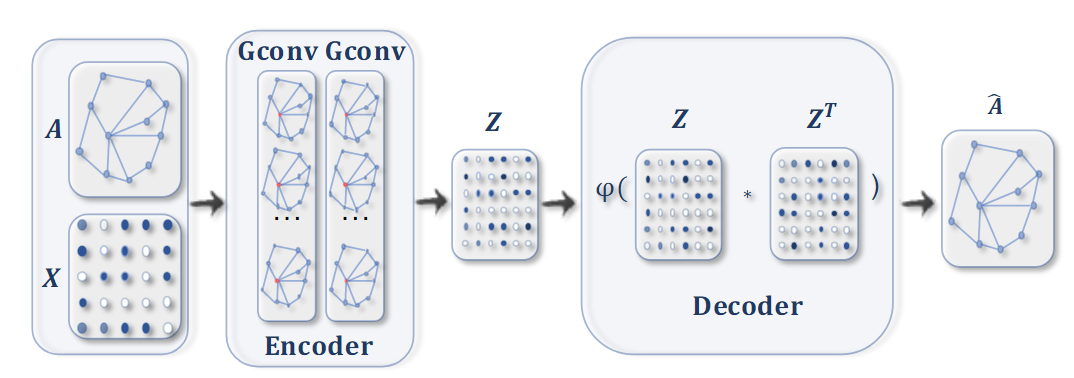
Codificador automático de gráficos para incrustación de red . Primero use la convolución de gráficos para obtener la incrustación de cada nodo, y luego el decodificador calcula la distancia por pares dada la incrustación. Después de aplicar la función de activación no lineal, el decodificador reconstruye la matriz de adyacencia del gráfico. La red es entrenada por minimizando la diferencia entre la matriz de adyacencia real y la matriz de adyacencia reconstruida.
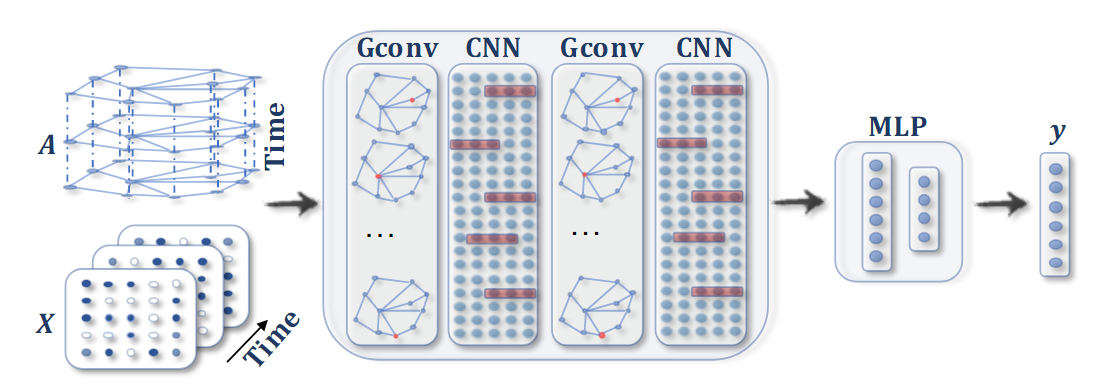
GNN espaciotemporal . Se aplica convolución al GNN en cada paso de tiempo, seguida de una capa 1D-CNN para extraer características temporales. La capa de salida es una transformación lineal que produce una predicción para cada nodo, como su futuro en el siguiente valor de paso de tiempo.
3. GNN recurrentes
Cyclic GNN es generalmente el trabajo pionero de GNN en sus inicios. Debido a la limitación de la cantidad de cálculo, generalmente se aplica a gráficos acíclicos dirigidos. Se propone The Graph Neural Network Model(IEEE Trans. Neural Network, 2009)un método más universal, que se puede aplicar a varios gráficos. Actualización de nodo El método es como sigue:
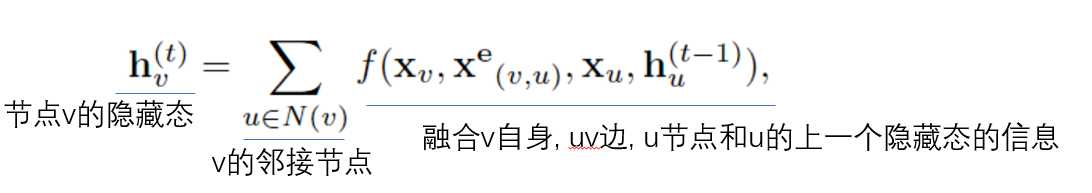
Para asegurar la convergencia, fff debe ser un mapa de contracción. SiffSi f es una red neuronal, se debe agregar una penalización.
Además, Gated GNN Gated graph sequence neural networks, (arxiv, 2015)utiliza la unidad de control (GRU) como se muestra arriba .La función f reduce el tiempo de convergencia y su actualización de nodo se compone de un mapeo lineal entre el estado oculto anterior y el estado oculto del nodo adyacente, de la siguiente manera:
hv ( t ) = GRU ( hv ( t − 1 ) , ∑ u ∈ N ( v ) W hu ( t − 1 ) ) h_v^{(t)} = GRU(h_v^{(t - 1)}, \ suma_ {u\in N(v)}Wh_u^{(t-1)})hv( t )=GR U ( hv( t − 1 ),tu ∈ norte ( v )∑wh _tu( t − 1 ))
El entrenamiento de esta red utiliza el descenso de gradiente mediante retropropagación a través del tiempo (el método de retropropagación de RNN).
En términos generales, el método del GNN cíclico es similar al RNN, que actúa en nodos discretos, pero la función de actualización ff utilizada por el GNN cíclico cada vez (capa)f es el mismo, por lo que se debe garantizar la convergencia.
4. GNN convolucionales
A diferencia del GNN cíclico, cada capa de GNN convolucional tiene diferentes parámetros que se pueden aprender, con un número fijo de capas, y la diferencia con el GNN cíclico es la siguiente:
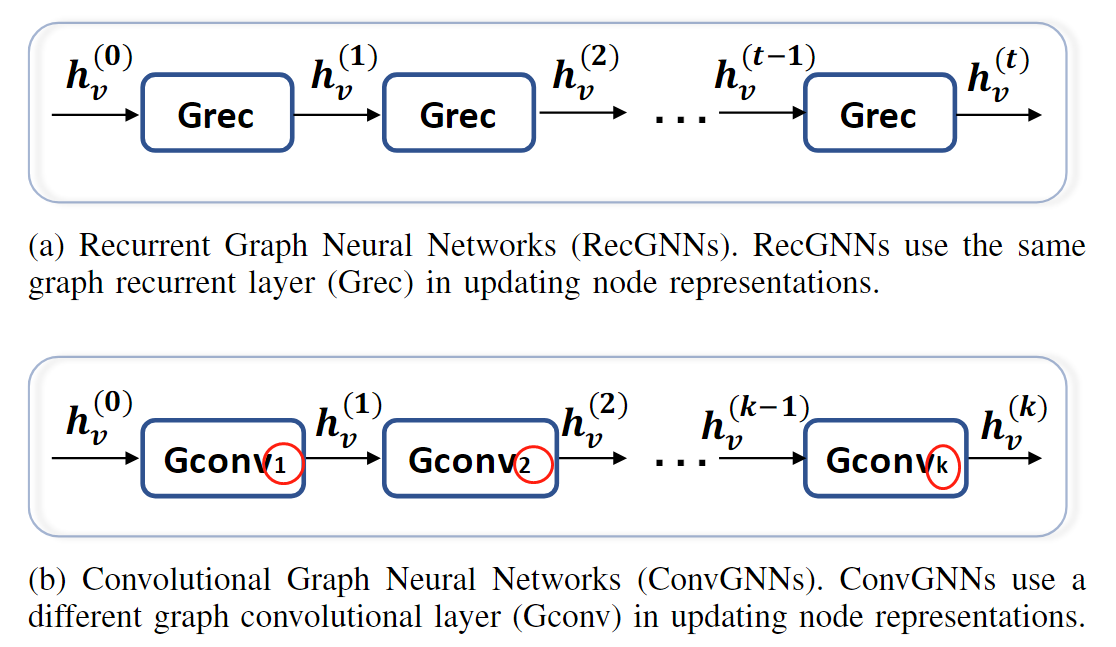
Los GNN convolucionales se dividen básicamente en dos categorías, basados en espectro (dominio de frecuencia) y basados en dominio espacial.
A. GNN convolucionales basados en espectros
GNN basado en espectro es básicamente para gráficos no dirigidos, podemos usar la matriz de Laplace del gráfico (normalizado) para representar de forma única las propiedades topológicas de este gráfico:
L = I n − D − 1/2 AD − 1/2 L = I_n - D^{-1/2}AD^{-1/2}l=Inorte−D− 1/2 AD_− 1/2
donde ddD es una matriz diagonal y cada elemento diagonal es la suma de las filas correspondientes de la matriz de adyacencia, es decir, el grado de este nodo.
Podemos ver que para la matriz de Laplace ( i , j ) (i, j)( yo ,j ) elementos:
sii = ji=ji=j ,ai, j = 0, di, j = grados (vi), li, j = 1 a_ {i,j} = 0, d_ {i,j} = grados (v_i), l_ {i,j} = 1ayo , j=0 ,dyo , j=grados mi gramo ( vyo) ,yoyo , j=1
sii ≠ ji \ne ji=j ,vi, vj v_i, v_jvyo,vj不相连, ai, j = 0, li, j = 0 a_{i,j} = 0, l_{i,j} = 0ayo , j=0 ,yoyo , j=0
sii ≠ ji \ne ji=j ,vi, vj v_i, v_jvyo,vj相连, ai, j = 1, li, j = − 1 / grados ( vi ) grados ( vj ) a_ {i,j} = 1, l_ {i,j} = -1/\sqrt{grados(v_i) grados (v_j)}ayo , j=1 ,yoyo , j=− 1/grados mi gramo ( vyo) grados mi gramo ( vj)
Por lo tanto, la matriz gráfica de Laplace puede representar de forma única la gráfica.
Es fácil ver que la matriz de Laplace es simétrica real, por lo que es semidefinida positiva, por lo que tiene valores propios no negativos. Podemos hacer una descomposición de valores propios en ella:
L = U Λ UTL = U \Lambda U^Tl=U Λ Ut
Por tanto, podemos definir la transformada de Fourier de un gráfico basándose en la descomposición de valores propios de la matriz de Laplace :
F ( x ^ ) = UT x ^ \mathcal{F}(\hat{x}) = U^T\hat{x}F (X^ )=Ud.tX^
Porque UUT = I UU^T = IU U Ut=I , por lo que la transformada de Fourier inversa del gráfico se puede definir inmediatamente:
F − 1 ( x ) = U x \mathcal{F}^{-1}(x)=UxF− 1 (x)=experiencia de usuario
Entonces, la transformada de Fourier del gráfico es en realidad transformar la señal del gráfico xxx se proyecta sobre una base ortonormal, en otras palabras,xxx se puede expresar comoUUCombinación lineal de vectores columna de U : x = ∑ ix ^ iuix = \sum_i \hat{x}_iu_iX=∑yoX^yotuyo, que es la relación entre la transformada de Fourier directa e inversa (consistente con la del procesamiento de señales).
Consideramos pasar la señal gráfica a través del filtro . Según el teorema de convolución (la transformada de Fourier de la convolución en el dominio del tiempo corresponde al producto en el dominio de la frecuencia), existen:
x ∗ g = F − 1 ( F ( x ) ⊙ F ( g ) ) = U ( UT x ⊙ UT g ) x * g = \mathcal{F}^{-1}(\mathcal{F}(x) \odot \mathcal{F}(g)) \\ = U(U^Tx \odot U^T g)X∗gramo=F− 1 (F(x)⊙F ( g ))=U ( UT x⊙Ud.T g)
donde⊙ \odot⊙ significa multiplicación por elementos. Si recordamosg θ = diag ( UT g ) g_{\theta} = diag(U^Tg)gramoi=diag ( U _ _T g), 则UT x ⊙ UT g = g θ UT x U^Tx \odot U^Tg = g_{\theta}U^TxUd.T x⊙Ud.t g=gramoiUd.Tx ,entonces
x ∗ g = U g θ UT xx * g = Ug_{\theta}U^TxX∗gramo=y el señoriUd.T x
La clave del GNN espectral es cómo elegir el filtro g θ g_{\theta}gramoi.
En la práctica, consideramos el kk -ésimo de la red.k capa, el número de canales de entrada y salida sonfk − 1, fk f_{k-1}, f_kFk - 1,Fk, entonces la capa jjLa salida de j canales es:
H : , j ( k ) = σ ( ∑ i = 1 fk − 1 U Θ i , j ( k ) UTH : , i ( k − 1 ) ) ∈ R n H^{(k)}_{:, j } = \sigma(\sum_{i=1}^{f_{k-1}}U\Theta_{i,j}^{(k)}U^TH^{(k-1)}_{:, i}) \en \mathbb{R}^nh: , j( k )=s (yo = 1∑Fk - 1U Θyo , j( k )Ud.T.H. _: , yo( k − 1 ))∈Rnorte
Θ i , j ( k ) \Theta_{i,j}^{(k)}Thyo , j( k )es una matriz diagonal y los elementos diagonales son un conjunto de parámetros que se pueden aprender.
Sin embargo, este enfoque tiene tres desventajas:
- Cualquier perturbación del gráfico tiene un gran efecto sobre los valores propios y los vectores propios (propiedad de la descomposición de valores propios)
- Los filtros aprendidos dependen del dominio, lo que significa que no se pueden aplicar a gráficos con estructuras diferentes.
- La complejidad de la descomposición de valores propios es alta ( O ( n 3 ) O(n^3)O ( n.3 )).
Para resolver el problema de alta complejidad, ChebNet y GCN reducen la complejidad a complejidad lineal mediante varias simplificaciones. ChebNet utiliza polinomios de Chebyshev para estimar el filtro g θ g_ {\ theta}gramoi, Ahora mismo
g θ = ∑ i = 1 K θ i T i ( Λ ~ ) , Λ ~ = 2 Λ / λ max − I n g_\theta = \sum_{i=1}^K \theta_i T_i(\tilde{\Lambda }), ~~\tilde{\Lambda} = 2\Lambda / \lambda_{max} - I_ngramoi=yo = 1∑kiyotyo(l~ ), l~=2 L/ minmáx _−Inorte
Así Λ ~ \tilde{\Lambda}lTodos los valores en ~ caen en[ − 1 , 1 ] [-1, 1][ -1 , _1 ]内. T i ( x ) T_i (x)tyo( x ) representa el polinomio de Chebyshev, que se define recursivamente de la siguiente manera:
T 0 ( x ) = 1 T_0(x) = 1t0( x )=1
T 1 ( x ) = x T_1(x) = xt1( x )=x
T yo ( x ) = 2 x T yo − 1 ( x ) − T yo − 2 ( x ) T_i(x) = 2xT_{i - 1}(x) - T_{i - 2}(x)tyo( x )=2 x Tyo − 1( x )−tyo − 2( x )
Introducido, el resultado de convolución del gráfico estimado según el polinomio de Chebyshev se obtiene de la siguiente manera:
x ∗ g = U ( ∑ i = 1 K θ i T i ( Λ ~ ) ) UT xx * g = U(\sum_{i=1}^K \theta_i T_i(\tilde{\Lambda}))U^ txX∗gramo=U (yo = 1∑kiyotyo(l~ ))UT x
Se puede demostrar por inducción matemática que la matriz polinómica de Chebyshev y la matriz de valores propios de la matriz de Laplace tienen la siguiente relación (?):
T i ( L ~ ) = UT i ( Λ ~ ) UT , L ~ = 2 L / λ max − I n T_i(\tilde{L}) = UT_i(\tilde{\Lambda})U^T, ~~ \tilde{L} = 2L / \lambda_{max} - I_ntyo(l~ )=UT _yo(l~ )Ud.T , l~=2 L / λmáx _−Inorte
Por lo tanto hay
x ∗ g = U ( ∑ i = 1 K θ i T i ( Λ ~ ) ) UT x = ∑ i = 1 K θ i T i ( L ~ ) xx * g = U(\sum_{i=1}^ K \theta_i T_i(\tilde{\Lambda}))U^Tx = \sum_{i=1}^K \theta_i T_i(\tilde{L})xX∗gramo=U (yo = 1∑kiyotyo(l~ ))UT x=yo = 1∑kiyotyo(l~ )x
Los filtros definidos por ChebNet son espacialmente locales, lo que significa que los filtros pueden extraer características locales independientemente del tamaño del gráfico. El espectro de ChebNet se asigna linealmente a [−1,1].
Veamos la red convolucional gráfica clásica GCN. GCN es una simplificación de ChebNet, tomando K = 1 K = 1k=1 , y suponiendo que el valor propio más grande es 2, obtenemos
x ∗ g = θ 0 x + θ 1 ( 2 L / λ max − I n ) x = θ 0 x + θ 1 ( 2 ( I n − D − 1 / 2 AD − 1 / 2 ) / λ max − I n ) x ( λ max = 2 ) = θ 0 x − θ 1 D − 1 / 2 AD − 1 / 2 xx * g = \theta_0x + \theta_1 (2L / \lambda_{max} - I_n)x \\ = \theta_0x + \theta_1 (2( I_n - D^{-1/2}AD^{-1/2}) / \lambda_{max} - I_n)x \\ (\lambda_{max} = 2) = \ theta_0x - \theta_1 D^{-1/2}AD^{-1/2}xX∗gramo=i0X+i1( 2 L / λmáx _−Inorte) x=i0X+i1( 2 ( yonorte−D− 1/2 AD_− 1/2 )/minmáx _−Inorte) x( yomáx _=2 )=i0X−i1D− 1/2 AD_− 1/2 x
Para reducir aún más la cantidad de parámetros y evitar el sobreajuste, suponga que θ = θ 0 = − θ 1 \theta = \theta_0 = -\theta_1i=i0=− yo1, hay inmediatamente
x ∗ g = θ ( I n + D − 1 / 2 AD − 1 / 2 ) xx * g = \theta(I_n + D^{-1/2}AD^{-1/2})xX∗gramo=θ ( yonorte+D− 1/2 AD_− 1/2 )x
Empíricamente, I n + D − 1/2 AD − 1/2 I_n + D^{-1/2}AD^{-1/2}Inorte+D− 1/2 AD_− 1/2 es probable que cause problemas de estabilidad, por lo que GCN usaD ~ − 1 / 2 A ~ D ~ − 1 / 2 \tilde{D}^{-1/2}\tilde{A}\tilde{D} ^{-1/2}D~− 1/2A~D~− 1/2 en su lugar, dondeA ~ = A + I n , D ~ \tilde{A} = A + I_n, \tilde{D}A~=A+Inorte,D~不A ~ \tilde{A}ALa matriz de grados de ~ .
Comprensión de esta normalización:
Dado que los elementos diagonales de la matriz de adyacencia son 0, θ ( I n + D − 1 / 2 AD − 1 / 2 ) x \theta(I_n + D^{-1/2} AD^{- 1/2})xθ ( yonorte+D− 1/2 AD_− 1/2 )xpuede considerarse como la información del nodo de agregación en sí, y el segundo elemento puede considerarse como la información de los nodos adyacentes. Sin embargo, esto causará inestabilidad, así que cambie la forma, eso es decir, agregue directamente el autobucle El borde del autobucle equivale a dar la matriz de adyacenciaAAA más la matriz identidadIn n I_nInorte.
El trabajo de seguimiento de GCN se centra principalmente en la selección de matrices simétricas.
B. GNN convolucionales basados en dominio espacial
De hecho, la convolución del gráfico en el dominio espacial es similar a la convolución de la imagen con una estructura espacial euclidiana típica, como se muestra en la siguiente figura:
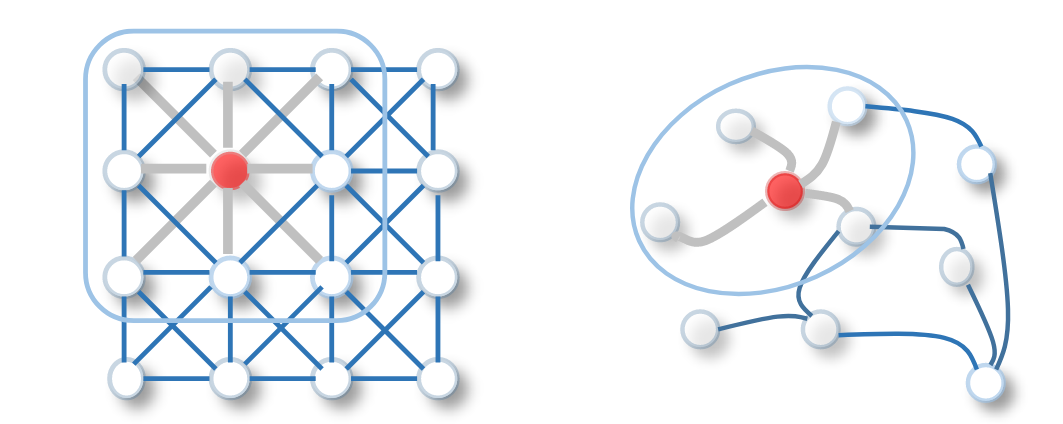
Por ejemplo, NN4G agrega la información de un nodo y sus nodos vecinos en cada iteración, como se muestra en la siguiente fórmula:
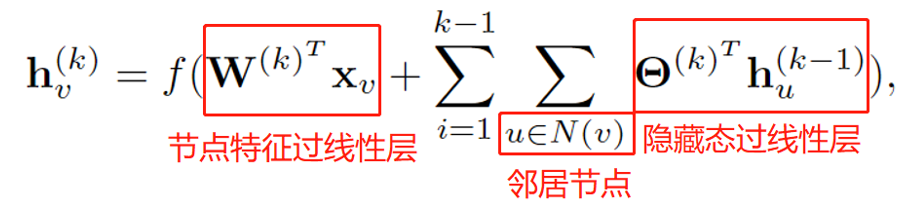
Además, existe un GNN de difusión más interesante, es decir, el proceso de convolución del gráfico se considera un proceso de difusión. En el proceso de difusión, la información se transmite de un nodo a otro de acuerdo con una cierta probabilidad, y esta probabilidad está relacionada con el grado del nodo, de la siguiente manera:
H ( k ) = f ( W ( k ) ⊙ P k X ) , P = D − 1 AH^{(k)} = f(W^{(k)} \odot P^kX), ~~P = D^{-1}Ah( k )=f ( W( k )⊙PAGkX ),_ PAG=D− 1 A
P = D − 1 AP = D^{-1}APAG=D− 1 El significado de Aes que para un punto con un grado grande, se enviará más información a los nodos vecinos conectados (el peso es mayor)
En Diffusion Graph Convolution, el resultado final es sumar los resultados intermedios, a saber:
H = ∑ k = 0 K f ( P k XW k ) H = \sum_{k=0}^Kf(P^kXW^k)h=k = 0∑kf ( pagk XWk )
PGC-DGCNN aprende pesos de acuerdo con la distancia entre nodos, es decir, para mejorar el papel de los nodos distantes. Específicamente, si el nodo vvv al nodouuLa longitud del camino más corto de u es jjj , luego registreS v , u ( j ) = 1 S_{v, u}^{(j)} = 1Sv , tu( j )=1 , en caso contrario 0.
Además, existe otra forma de GNN en el espacio aéreo, que se conoce como paso de mensajes . El paso de mensajes se puede interpretar como que la información se puede transmitir desde los nodos a lo largo de los bordes; en términos generales, hay un KK fijo.Iteraciones de K pasos, para que la información se pueda transmitir más lejos, es decir, hay un campo receptivo más grande, se puede expresar mediante la siguiente fórmula:
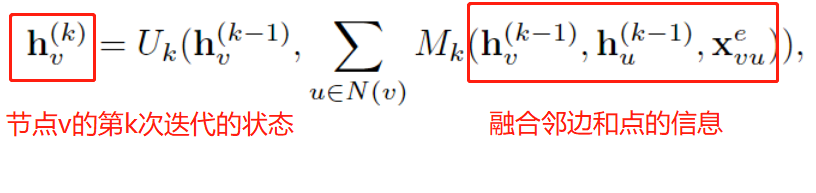
Sin embargo, para tareas a nivel de gráfico, el paso de mensajes tradicional no puede distinguir entre diferentes estructuras de gráficos. Para este fin, GIN ajusta el peso del nodo central, distinguiendo así el nodo central y los nodos vecinos, de la siguiente manera:

Además, para los nodos vecinos de un nodo, la importancia de diferentes vecinos puede ser diferente, por lo que GAT propone un mecanismo de atención de gráficos, que convierte el peso de los nodos vecinos en un parámetro que se puede aprender durante la agregación:
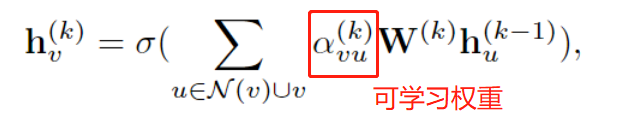
en
α vu ( k ) = softmax ( g ( a T [ W ( k ) hv ( k − 1 ) ∣ ∣ W ( k ) hu ( k − 1 ) ] ) ) \alpha_{vu}^{(k)} = softmax(g(a^T[W^{(k)}h_{v}^{(k-1)}||W^{(k)}h_{u}^{(k-1)}]) )avu( k )=so f t ma x ( g ( aT [W( k ) hv( k − 1 )∣∣W _( k ) htu( k − 1 )]))
Capa de agrupación de gráficos, autocodificador de gráficos que se actualizará...