Complejidad temporal-complejidad espacial de la estructura de datos

Para implementar algunos proyectos, los datos deben almacenarse en la memoria.La estructura de datos es la forma en que las computadoras almacenan y organizan los datos . Se refiere a una colección de elementos de datos que tienen una o más relaciones específicas entre sí. por ejemplo: matriz, lista enlazada, árbol...

1.2 ¿Qué es un algoritmo?

Un algoritmo es simplemente una serie de pasos computacionales utilizados para transformar los datos de entrada en resultados de salida . Los algoritmos comunes son: clasificación, búsqueda, comprobación de duplicados, algoritmo de recomendación...

1.3 La importancia de las estructuras de datos y los algoritmos

Habrá muchas preguntas sobre estructuras de datos y algoritmos en la prueba escrita de reclutamiento escolar.

Puedes echar un vistazo al enlace, en un trabajo futuro:

La importancia de las estructuras de datos y los algoritmos para un programador

1.4 Cómo aprender bien la estructura de datos y el algoritmo

<1> Escriba más códigos

<2>Presta atención a dibujar y pensar.

2. Eficiencia del algoritmo

La eficiencia del algoritmo depende de dos puntos. El primer punto es la eficiencia del tiempo, es decir, la complejidad del tiempo . El segundo punto es la eficiencia del espacio, es decir, la complejidad del espacio. Sin embargo, con el desarrollo de la industria informática, la capacidad de almacenamiento de la computadora ha alcanzado un nivel muy alto, por lo que ahora no tenemos que prestar demasiada atención a la complejidad espacial de un algoritmo

3. Complejidad del tiempo

3.1 El concepto de complejidad temporal

La complejidad temporal de un algoritmo es una expresión de función con un número desconocido en matemáticas . La complejidad de un algoritmo no depende del tiempo de ejecución del algoritmo, porque el tiempo de ejecución específico es diferente en diferentes entornos , por ejemplo: hace 10 años, CPU de 2 núcleos, el tiempo de funcionamiento de una máquina con memoria de 2 g es diferente al de la máquina actual con CPU de 8 núcleos y memoria de 8 g. El número de ejecuciones de las operaciones básicas en el algoritmo es la complejidad temporal del algoritmo.

3.2 Representación asintótica de la gran O

Calcule cuántas veces se realiza la operación básica de Func1.

void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
 for (int j = 0; j < N ; ++ j)
 {
 ++count;
 }
}
for (int k = 0; k < 2 * N ; ++ k)
{
 ++count;
}
int M = 10;
while (M--)
{
 ++count;
}
printf("%d\n", count);
}

Número de operaciones básicas realizadas por Func1: F(N)=N*N+2*N+10

Cuando N = 10 F(N) = 130

Cuando N = 100 F(N) = 10210

Cuando N = 1000 F(N) = 1002010

Cuanto mayor es N, menor es la influencia de los dos últimos elementos en el resultado, por lo que, al calcular la complejidad del tiempo, solo necesitamos un número aproximado de ejecuciones, por lo que aquí usamos la representación asintótica (estimación) de O grande , es decir, la complejidad del tiempo: O( N^2)

Notación asintótica Big O:

(1) Reemplace todas las constantes aditivas en tiempo de ejecución con la constante 1

(2) En la función de número de corridas modificada, solo se mantiene el término de mayor orden

(3) Si existe el orden más alto y no es 1, elimine la constante multiplicada por este elemento

[Ejemplo 1]: Complejidad temporal de doble bucle: O(N)

Debería haber sido 2*N, de acuerdo con la representación asintótica de O grande (3) simplificada a O(N)

// 计算Func2的时间复杂度？
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}

[Ejemplo 2]: Complejidad temporal de doble bucle: O(N+M)

(Si la premisa: M>>N, entonces la complejidad del tiempo es O(M);

N>>M, entonces la complejidad del tiempo es O(N);

M y N son similares, por lo que la complejidad temporal O(M) u O(N) está bien)

En general, N se utiliza para las incógnitas en los cálculos de complejidad temporal, pero también se pueden utilizar M, K, etc.

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}

[Ejemplo 3]: Complejidad temporal de bucle constante: O(1)

Originalmente 100, según la notación asintótica O grande (1) simplificada a O(1)

( O(1) no significa que el algoritmo se ejecute una vez, sino un número constante de veces )

// 计算Func4的时间复杂度？
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}

[Ejemplo 4]: Complejidad temporal de strchr: O(N)

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

La lógica de la función strchr es en realidad la siguiente

mientras （*str）

{

si (*str==carácter)

devolver str;

demás

++cadena;

}

Tome la cadena hello world como ejemplo:

Suponga que está buscando h: 1 Mejor caso: número mínimo de ejecuciones para cualquier tamaño de entrada (límite inferior)

Suponiendo que está buscando w: N/2 caso promedio: el número esperado de ejecuciones de cualquier tamaño de entrada (probablemente la mejor y la peor suma/2)

Suponga que está buscando d: N Peor caso: número máximo de ejecuciones para cualquier tamaño de entrada (límite superior)

Cuando un algoritmo tiene una complejidad de tiempo diferente según la entrada, la complejidad de tiempo se espera de manera pesimista y se ve el peor de los casos (es decir, la complejidad de tiempo de este ejemplo es O (N))

[Ejemplo 5]: Complejidad temporal de la clasificación de burbujas: O(N^2)

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
} 
}

Complejidad temporal: N-1, N-2, N-3...1 El valor exacto es N*(N-1)/2, luego la representación del gradiente de O grande es O(N^2)

Para calcular la complejidad del tiempo, no puedes simplemente mirar algunas capas de bucles, sino mirar sus pensamientos.

[Ejemplo 6]: Complejidad temporal de búsqueda binaria: O(log2N)

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}

Mejor caso: O(1)

Peor caso: O(log2N)

¿Por qué es O(log2N)?

[Comprensión de la imagen] : supongamos que queremos buscar X veces, el tamaño de una matriz es N, si no se encuentra cada búsqueda binaria, N se dividirá entre 2, considerando el peor resultado, luego hasta que N se divida hasta que solo quede 1 se acabó

N/2/2/2/2...=1

2^X=N

X=log2N

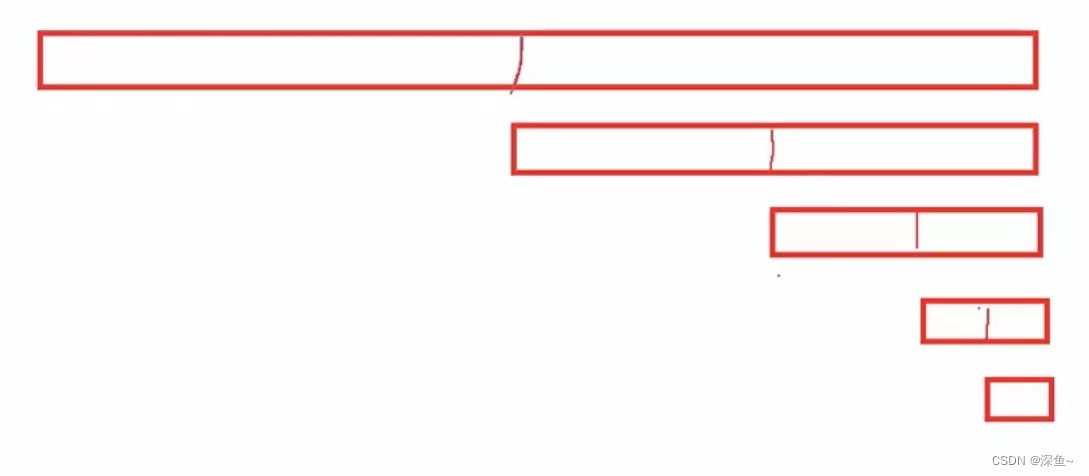
Se puede ver que el algoritmo de búsqueda binaria es un algoritmo muy poderoso.

Buscar en N números Número aproximado de búsquedas

1000 10

100W 20

1 billón 30

Pero la premisa de este algoritmo es que la matriz está ordenada

[Ejemplo 7]: Complejidad temporal de la recursividad factorial: O(N)

Complejidad temporal del algoritmo recursivo: número de recursividad * número de cada llamada recursiva

// 计算阶乘递归Factorial的时间复杂度？
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}

Hacer (N) Hacer (N-1) ... Hacer (1)

[Ejemplo 8]: Complejidad temporal de la recursividad de Fibonacci: O(2^N)

// 计算斐波那契递归Fibonacci的时间复杂度？
long long Fibonacci(size_t N)
{
return N < 2 ? N : Fibonacci(N-1)+Fibonacci(N-2);
}

[Comprensión de la imagen]: comprenda el pensamiento lógico de la recursión. Cada recursión llamará a dos pequeñas recursiones. Finalmente, la llamada recursiva de la derecha terminará primero. Luego, el número de recurrencias es la suma de la secuencia geométrica menos la esquina inferior derecha. el número de veces

Fib（N）=2^0+2^1+2^2+...+2^nX

El número de llamadas recursivas aquí es una constante, lo que equivale a no *

Entonces la gran notación asintótica O es O(2^N)

Se puede ver que el método de escritura recursiva de la secuencia de Fibonacci es un algoritmo completamente inútil porque es demasiado lento

4. Complejidad espacial

La complejidad del espacio también es una expresión matemática, que es una medida del espacio de almacenamiento adicional temporal ocupado por un algoritmo durante la operación.

La complejidad del espacio no es cuántos bytes ocupa el programa, porque esto no es muy significativo, entonces la complejidad del espacio es el número de variables

Las reglas de cálculo de la complejidad del espacio son básicamente similares a las de la complejidad del tiempo, y también se utiliza la notación asintótica de la O grande.

[Nota]: El espacio de pila (parámetros de almacenamiento, variables locales, cierta información de memoria, etc.) requerido por la función en tiempo de ejecución se ha determinado durante la compilación, por lo que la complejidad del espacio está determinada principalmente por la función que solicita espacio adicional en tiempo de ejecución.

[Ejemplo 1]: Complejidad espacial del tipo burbuja: O(1)

Hay tres variables en el tipo de burbuja: intercambio, fin, i, luego, de acuerdo con la notación progresiva O grande, es O (1)

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}

[Ejemplo 2]: Complejidad espacial de la recursividad de Fibonacci: O(N)

Una matriz de N números abre dinámicamente N+1 espacios, y la complejidad del espacio después de la simplificación es O(N)

Esta función devuelve una matriz de los primeros n elementos de la secuencia de Fibonacci, no un número

La complejidad temporal de esa función es O(N), que es mucho más simple que la recursiva O(2^N)

// 计算Fibonacci的空间复杂度？
//返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray =
(long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
}
return fibArray ;
}

[Ejemplo 3]: Complejidad espacial de recursividad factorial de funciones: O(N)

// 计算阶乘递归Factorial的空间复杂度？
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}

[Comprensión de la imagen]: la función recursiva se llama N veces, y se abren N marcos de pila, y cada marco de pila usa un espacio constante, por lo que la complejidad del espacio es O (N) (solo mire la profundidad de la recursividad )

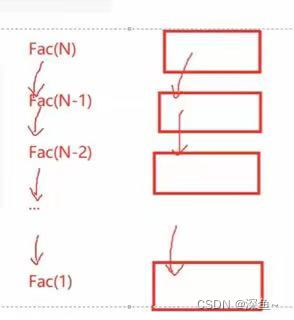
[Expansión] La complejidad espacial de la secuencia recursiva de Fibonacci: O(N)

// 计算斐波那契递归Fibonacci的空间复杂度？
long long Fibonacci(size_t N)
{
return N < 2 ? N : Fibonacci(N-1)+Fibonacci(N-2);
}

[Comprensión de la imagen]: el orden de este espacio de llamada de función es Fbi(N), Fbi(N-1)...Fbi(1), que es la rama más a la izquierda, y luego el espacio de estas funciones se destruye y continúa a la siguiente se bifurca, de modo que la profundidad de recursión de la función sea siempre N, no 2 ^ N

El espacio se puede reutilizar y no acumular

El tiempo se ha ido para siempre, acumulado

Esta vez, el contenido de la complejidad temporal y espacial de la estructura de datos está aquí. Si tiene alguna pregunta, dé la bienvenida al área de comentarios o mensaje privado para comunicarse. Creo que la escritura del autor no es mala, o he ganado un poco. poco Vengo a un clic de tres enlaces, ¡muchas gracias!