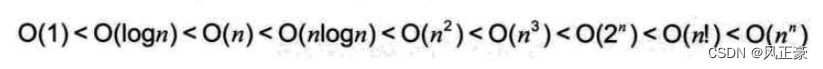Estructura de datos (2.1) - cálculo de la complejidad del tiempo y la complejidad del espacio

prefacio

(1) Debido al blog anterior: estructura de datos (2): el algoritmo tiene muy poca explicación para el cálculo de la complejidad del tiempo y la complejidad del espacio. Así que agregaré múltiples explicaciones de casos nuevamente.
(2) El artículo anterior ya ha presentado en detalle por qué nuestro algoritmo utiliza el concepto de complejidad. Por lo tanto, mi artículo se centrará en cómo calcular la complejidad.

Cálculo de la complejidad del tiempo

(1) Como se mencionó en el blog anterior, en circunstancias normales, no consideraremos la complejidad del espacio. Así que me centraré en el cálculo de la complejidad del tiempo.
(2) Como dijimos antes, la complejidad temporal es el método de la O grande utilizado . (Nota: si no lo entiende, lea la parte de la complejidad del tiempo del algoritmo en el artículo anterior. Ya lo he presentado en detalle). (3) A
continuación, iré directamente al código para el cálculo. Publicaré el código primero, luego lo explicaré. Si está interesado, puede mirar el código y calcularlo primero, y luego mirar el análisis.

Ejemplo 1—Capacitación de introducción

void Func1(int N)
{
    
    
	int count = 0;
	for (int i = 0; i < N ; ++ i)
	{
    
    
		for (int j = 0; j < N ; ++ j)
		{
    
    
			++count;
		}
	}
	for (int k = 0; k < 2 * N ; ++ k)
	{
    
    
		++count;
	}
	int M = 10;
	while (M--)
	{
    
    
		++count;
	}
	printf("%d\n", count);
}

(1) Según el método de cálculo Big O, sabemos que primero debemos encontrar el tiempo de ejecución específico de esta función.
(2) Primero, vemos que dos declaraciones for están anidadas, la primera declaración for debe ejecutarse N veces, y la segunda declaración for está anidada adentro, por lo que el número final de ejecuciones es N^2 veces.

	for (int i = 0; i < N ; ++ i)  //执行N次
	{
    
    
		for (int j = 0; j < N ; ++ j)  //执行N*N次，所以最终结果是执行了N^2次
		{
    
    
			++count;
		}
	}

(3) No hay anidamiento en la segunda instrucción for, se considera que la condición es <2*N y se incrementa a 1 cada vez. Por lo tanto, debe ejecutarse 2N veces aquí.

	for (int k = 0; k < 2 * N ; ++ k)
	{
    
    
		++count;
	}

(4) Ejecute M veces en el último tiempo, y M recibe una constante de 10. Entonces este while se ejecuta 10 veces.

	int M = 10;
	while (M--)
	{
    
    
		++count;
	}

(5) En resumen, la conclusión final es que el número de ejecuciones de este código es el siguiente
$$T（norte）={norte}^2+2norte+10$$
(6) De acuerdo con el método Big O, se puede ver que cuando f(n) es n^2. n tiende a infinito, y finalmente T(n)/f(n) es una constante. Entonces la complejidad del tiempo es O (n ^ 2).
(7) En resumen, el método de cálculo Big O es retener la mayor cantidad de palabras de ejecución de código.

Ejemplo 2: la constante del término más alto no es única

void Func2(int N)
{
    
    
	int count = 0;
	for (int k = 0; k < 2 * N ; ++ k)
	{
    
    
		++count;
	}
	int M = 10;
	while (M--)
	{
    
    
		++count;
	}
	printf("%d\n", count);
}

(1) Del mismo modo, primero calcule los tiempos de ejecución generales de esta función.
(2) Para el primer ciclo for, la condición de juicio es k < 2 * N, y K se incrementa a 1 cada vez, por lo que debe ejecutarse 2N veces.

	for (int k = 0; k < 2 * N ; ++ k)
	{
    
    
		++count;
	}

(3) De manera similar, este while se ejecuta 10 veces.

	int M = 10;
	while (M--)
	{
    
    
		++count;
	}

(4) Por lo tanto, los tiempos finales de ejecución de esta función son 2N+10. Entonces, de acuerdo con el método Big O, ¿es esta complejidad de tiempo O (2N)?
(5) Viendo lo que dije, entonces la respuesta debe ser incorrecta. El método de cálculo Big O estipula que si la constante del término más alto no es 1, se debe eliminar la constante más alta. Por ejemplo, el elemento más alto de esta pregunta es N y su constante es 2, por lo que la complejidad temporal de esta pregunta es O(N).

Ejemplo 3: aparecen varias variables

void Func3(int N, int M)
{
    
    
	int count = 0;
	for (int k = 0; k < M; ++ k)
	{
    
    
		++count;
	}
	for (int k = 0; k < N ; ++ k)
	{
    
    
		++count;
	}
	printf("%d\n", count);
}

(1) Para este tema, encontraremos que hay dos variables, entonces, ¿cómo calcular la complejidad del tiempo? De hecho, no es tan complicado como se imagina, solo hay que analizar según la situación.
(2) Primero, suponiendo que N y M tienen aproximadamente el mismo tamaño, entonces la complejidad temporal es O(N+M).
(3) Segundo, suponiendo que N es mucho mayor que M, entonces la complejidad temporal es O(N).
(4) En segundo lugar, suponiendo que N es mucho menor que M, entonces la complejidad temporal es O(M).

Ejemplo 4 - número único de ejecuciones

void Func4(int N)
{
    
    
	int count = 0;
	for (int k = 0; k < 100; ++ k)
	{
    
    
		++count;
	}
	printf("%d\n", count);
}

(1) Cuando observamos esta función, encontraremos que el parámetro formal entrante N no se usa. En otras palabras, esta función está fijada para ejecutarse 100 veces.
(2) Para esta situación, algunas personas pueden estar un poco confundidas. Entonces, ¿cuál es su complejidad de tiempo?
(3) El método de cálculo Big O estipula que si es una función con un número fijo de ejecuciones. La complejidad del tiempo es O(1).

Ejemplo 5—Múltiples casos de tiempos de ejecución

const char * strchr ( const char * str, int character )
{
    
    
	while(*str != '\0')
	{
    
    
		if(*str == character)
		{
    
    
			return str;
		}
		str++;
	}
	return NULL;
}

(1) Primero explique la función de esta función. Supongamos que tenemos una cadena "sdyzscx", quiero encontrar el carácter 'y' de esta cadena, luego atravesará esta cadena. Si se encuentra el carácter 'y', se devolverá la posición de ese carácter. De lo contrario, se devuelve un puntero nulo.
(2) Para este tema, encontraremos que es difícil encontrar su tiempo de ejecución específico. Porque asumiendo que el carácter que estamos buscando es siempre el primer carácter de la cadena, entonces el conteo de palabras de ejecución de esta función siempre es 1, y la complejidad del tiempo es O(1).Llamamos a esta situación el mejor de los casos.
(3) Pero si el carácter que buscamos siempre aparece en la posición media cada vez, es decir, solo necesita ejecutarse N/2 veces.Esto se llama el caso promedio.
(4) La última es que mantenemos una actitud absolutamente pesimista, asumiendo que el carácter que buscamos será siempre el último carácter de la cadena, o no se encontrará. Entonces el número de ejecuciones es N, y la complejidad del tiempo es O(n).Esto se llama el peor de los casos.
(5) En la práctica, generalmente prestamos atención a la peor situación de funcionamiento, por lo que la complejidad temporal de esta pregunta es O(n).

Ejemplo 6: el número de ejecuciones no es intuitivo

void BubbleSort(int* a, int n)
{
    
    
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
    
    
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
    
    
			if (a[i-1] > a[i])
			{
    
    
				Swap(&a[i-1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

(1) Este es un algoritmo de clasificación de burbujas, pero encontraremos que parece que el número de ejecuciones de este tema no es fácil de calcular. En este momento, la mejor manera es incorporar valores específicos.
(2) Suponga que n es 10 y hay 10 elementos en la matriz entrante.
<1> Para la primera ejecución, la primera declaración for ingresa el juicio, y el final del juicio de la segunda declaración for es 10. Así que aquí se ejecuta 9 veces.
<2> La segunda carrera, esta vez, termina en 9. Luego, la segunda instrucción for se ejecuta 8 veces.
<3> ¡Por analogía, podemos saber que aquí está la implementación de 9! (Tenga en cuenta que '!' significa factorial, si no entiende, puede leer libros de texto de la escuela secundaria).
<4> Si el número específico se convierte en la variable n, se puede concluir que el número real de ejecuciones de esta función es: (n-1)! Según el conocimiento de la escuela primaria, podemos saber que el número de ejecuciones es
$$\frac{(n-1+1)(norte-1)}{2}=\frac{{norte}^2-}{2}$$
<5> Según el método Big O, la complejidad de tiempo final es O(n^2)

Ejemplo 7 - Complejidad temporal de la búsqueda binaria

/* 作用：二分查找，用于寻找有序数组的值
 * 传入参数 ： 
     * a ： 有序数组的首元素地址
     * n ： 该元素的长度
     * x ： 要查找的元素
 * 返回值 ： 如果找到了元素，返回该元素在数组的第几项。没有找到元素，返回-1。
*/
int BinarySearch(int* a, int n, int x)
{
    
    
	assert(a);
	int begin = 0;
	int end = n-1;
	while (begin < end)
	{
    
    
		int mid = begin + ((end-begin)>>1);
		if (a[mid] < x)
			begin = mid+1;
		else if (a[mid] > x)
			end = mid;
		else
			return mid;
	}
	return -1;
}

(1) Esta función es una función de búsqueda binaria para una secuencia ordenada .
(2) Al ver esta función, todavía no tengo ninguna idea, así que sigo configurando los números directamente. Supongamos que hay una secuencia [0,1,2,3,4,5,6,7,8,9], porque la complejidad del tiempo de cálculo se calcula de acuerdo con la peor condición, así que supongamos que el número que necesitamos encontrar es 0 .
<1> Primero, pase esta matriz, begin es 0 y end es 9 (tenga en cuenta que end es 9, pero es el último elemento de la matriz puntiaguda, porque el primer elemento de la matriz comienza en 0). mid = (9-0) >> 1 = 4, por lo que min apunta al elemento 4.

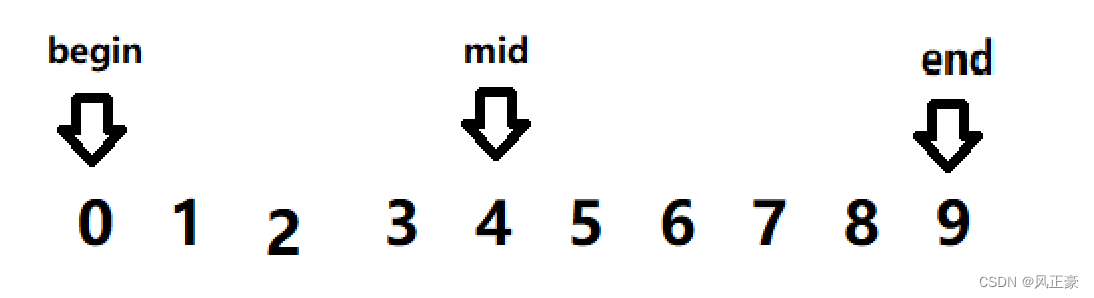
<2> Encontraremos que 0 es menor que 4, entonces end=mid=4. medio=0+(4-0)>>1=2.

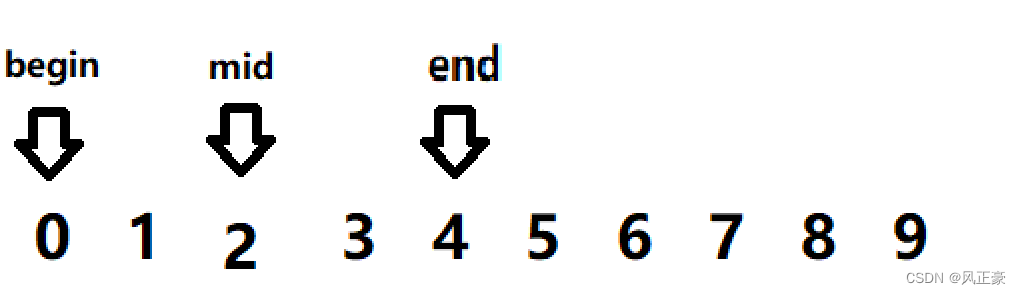
<2> En este momento, aún encontraremos que 0 es menor que 2, por lo que end=mid=2. medio=0+(2-0)>>1=1.

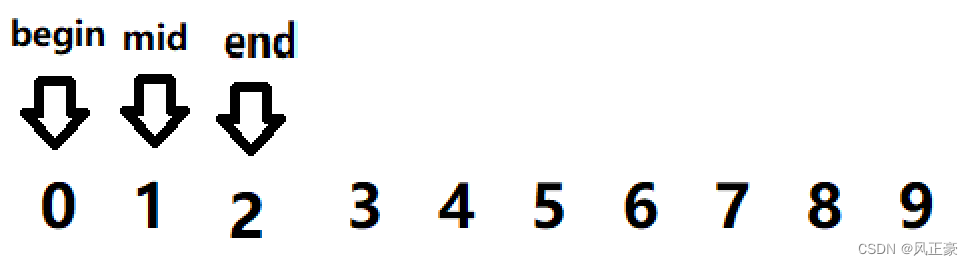
<3>0 sigue siendo menor que 1, por lo que end=mid=1. medio=0+(1-0)>>1=0.

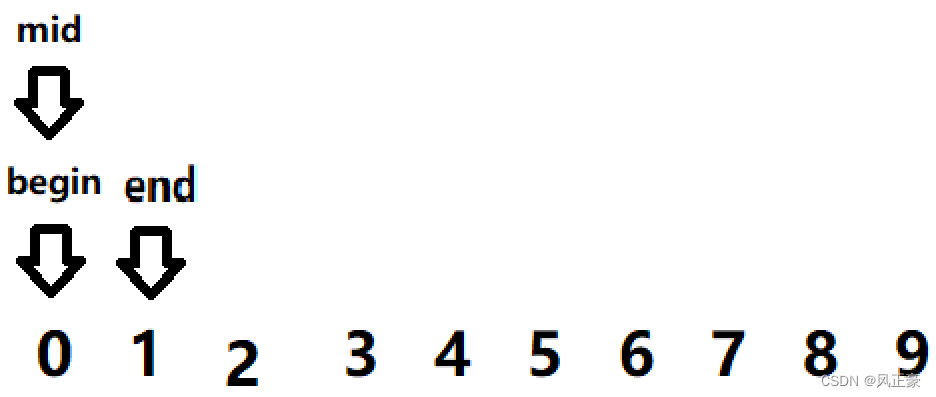
<4> Finalmente, encontraremos que a[mid] == 0, y se devuelve el valor.
(3)
<1>Según el ejemplo anterior, encontraremos que el peor de los casos debe ejecutarse 4 veces.
<2> Por lo tanto, asumimos que una matriz ordenada tiene elementos N. Dado que discutimos el peor de los casos, la mitad de los datos se excluyen cada vez que buscamos.
<3> Para la primera búsqueda, todavía quedan N/2 elementos.
<4> Para la segunda búsqueda, todavía quedan N/4 elementos.
<5> Por analogía, asumimos que el peor de los casos es encontrar X veces. Luego, finalmente satisfaga la condición 2^(X-1)<N<2 ^X, luego se encuentra X.
<6> Por lo tanto, la complejidad del tiempo satisface la siguiente fórmula, pero en raras ocasiones, algunos libros de estructura de datos se escriben con la siguiente fórmula. (Nota: ¡es diferente de la forma de escribir matemáticas! No es riguroso, pero a menudo se considera igual)
$$O\left({log\_{\_}_{}}^{norte}\right)=Acerca\; de\left(l{g}_{}\right)$$

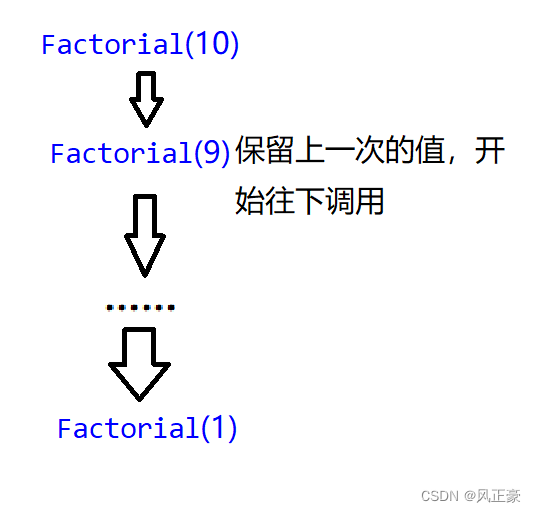
Ejemplo 8 - Complejidad temporal de llamar recursivamente a una función

long long Factorial(size_t N)
{
    
    
	return N < 2 ? N : Factorial(N-1)*N;
}

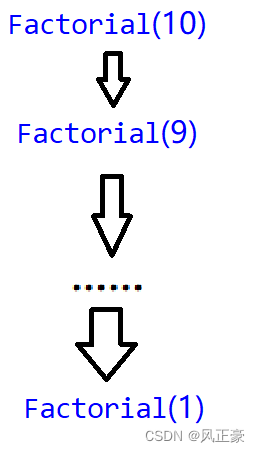
(1) Todavía es imposible ver el resultado directamente, y aún es necesario establecer valores específicos para encontrar ideas. Supongamos que N es 10. Entonces su relación de llamada de función es la siguiente.
(2) Encontraremos que el número de ejecuciones es el número de N pasados. Entonces la complejidad del tiempo es O(N).

Cálculo de la complejidad del espacio

Ejemplo 1—Entrenamiento básico

(1) Después de leer tantos ejemplos anteriores, deberíamos tener una mejor comprensión del cálculo de la complejidad del tiempo. Entonces, ¿cómo calcular la complejidad del espacio? Tome el siguiente ejemplo para comenzar el cálculo.
(2) La complejidad del espacio también es el método de cálculo de Big O. Primero, contemos cuántas variables se establecen en la siguiente función.
(3) Vemos que solo se crea un intercambio de variables en esta función, pero este intercambio está en el ciclo for, entonces, ¿la complejidad espacial de esta función es O(N)?

void BubbleSort(int* a, int n)
{
    
    
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
    
    
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
    
    
			if (a[i-1] > a[i])
			{
    
    
				Swap(&a[i-1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

(4) La respuesta es incorrecta, porque en la estructura de datos se acumula tiempo, pero no se acumula espacio . Algunas personas pueden confundirse cuando ven esta oración. ¿Qué significa eso?
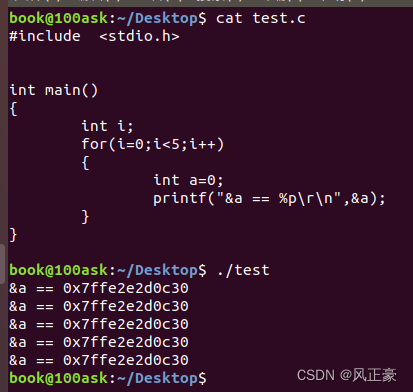
(5) Antes que nada, necesitamos saber que aunque la variable de intercambio está en el bucle for, cada bucle for no crea una variable de intercambio, sino que reutiliza el mismo espacio . Como se muestra en la siguiente figura, por lo tanto, la complejidad del espacio aquí es O(1).

Ejemplo 2: Cálculo de la complejidad del espacio para llamadas recursivas

long long Factorial(size_t N)
{
    
    
	return N < 2 ? N : Factorial(N-1)*N;
}

(1) Con base en el conocimiento anterior, ¿cuál es la complejidad espacial de esta función?
(2) La respuesta es muy sencilla, O(N). ¿por qué? Porque al llamar recursivamente, cada llamada de función conservará el último valor.

(3) Cuando finalmente se llama a Factorial(1), la llamada a la función finaliza, comienza el retorno y las variables anteriores comienzan a destruirse.

Ejemplo 3—Cálculo de la complejidad espacial de la función malloc

long long* Fibonacci(size_t n)
{
    
    
	if(n==0)
		return NULL;
	long long * fibArray =(long long *)malloc((n+1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; ++i)
	{
    
    
		fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
	}
	return fibArray ;
}

(1) Esta es una secuencia de Fibonacci, ¿cuál es la complejidad del espacio?
(2)De hecho, para este tipo de cálculo de complejidad espacial y complejidad temporal, lo más importante es ver si esta función tiene algo que ver con los parámetros entrantes.. Si no hay relación, entonces la alta probabilidad es O(1). Si hay una relación, solo necesita mirar la parte que está relacionada.
(3) Encontraremos que en esta función, solo la función malloc está relacionada con el parámetro entrante n, por lo que de hecho necesitamos leer la oración de malloc. Debido a que los datos solicitados por malloc son n+1, la complejidad espacial de esta función es O(N) y no es necesario buscar en otros lugares.

Resumir

(1) Tanto la complejidad del tiempo como la complejidad del espacio se basan en el método de cálculo Big O. El cálculo de complejidad solo necesita mirar la parte relacionada con los parámetros pasados ​​por la función .
(2) Puntos clave de la complejidad del tiempo:
<1> Solo es necesario mirar el elemento más alto.
<2> La constante del elemento más alto se puede ignorar.
<3> La complejidad del tiempo generalmente solo analiza el peor de los casos.
(3) Puntos clave de la complejidad del espacio:
<1> El tiempo es acumulativo, pero el espacio no.
<2> En general, solo consideramos la complejidad del tiempo, no la complejidad del espacio.
(4) Según la complejidad, podemos medir bien las ventajas y desventajas de un algoritmo, y el tiempo de ejecución de diferentes complejidades de tiempo aumenta de pequeño a grande.