Capítulo 2 Complejidad espacial y temporal de los algoritmos
1. Eficiencia algorítmica
¿Cómo medir la calidad de un algoritmo?
Generalmente , se mide por la complejidad temporal y la complejidad espacial del algoritmo.
La complejidad del tiempo mide principalmente qué tan rápido se ejecuta un algoritmo , mientras que la complejidad del espacio mide principalmente el espacio extra requerido para ejecutar un algoritmo . En los primeros días del desarrollo de las computadoras, la capacidad de almacenamiento de las computadoras era muy pequeña. Así que está muy preocupado por la complejidad del espacio. Pero después del rápido desarrollo de la industria informática,
la capacidad de almacenamiento de la computadora ha alcanzado un nivel muy alto. Así que ya no necesitamos prestar especial atención a la complejidad espacial de un algoritmo .
2 tiempos de complejidad
2.1 El concepto de complejidad temporal
Definición: en informática, la complejidad temporal de un algoritmo es una función que describe cuantitativamente el tiempo de ejecución de ese algoritmo. El número de ejecuciones de las operaciones básicas en el algoritmo es la complejidad temporal del algoritmo.
Es decir: encontrar la expresión matemática entre un determinado enunciado básico y el tamaño del problema N, es calcular la complejidad temporal del algoritmo.
ejemplo:
P: ¿Cuántas veces se ejecuta la instrucción ++count en Func1?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
++count;
}
}
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
}
El número de ejecuciones se expresa como una función de la siguiente manera:
F(N) = N^2^ + 2 * N + 10Desde la perspectiva de las funciones matemáticas,
la imagen de 2 * N + 10 al resultado final de la operación de la función se hace cada vez más pequeño a medida que aumenta N. Cuando el área de N es infinita, incluso podemos ignorarlo, es decir, el resultado final de la función tiende a N. Sólo está relacionada con N 2
.
2.2 Notación asintótica para Big O
Notación Big O: es una notación matemática utilizada para describir el comportamiento asintótico de una función.
Derive el método de la O grande:
- Reemplace todas las constantes aditivas en tiempo de ejecución con la constante 1 (si el número de ejecuciones de la declaración básica de una función es una cierta constante).
- En la función de tiempos de ejecución modificados, solo se conservan los términos de mayor orden.
- Si existe el término de mayor orden y no es 1, elimine la constante multiplicada por este término (es decir, elimine el coeficiente del término de mayor orden). El resultado es una orden O grande.(La complejidad del tiempo se mide en órdenes de magnitud)
Después de usar la notación asintótica de O grande, la complejidad temporal de Func1 es:
O (N 2 )
A través de lo anterior, encontraremos que la representación asintótica de O grande elimina aquellos elementos que tienen poco efecto en el resultado, y muestra el número de ejecuciones de manera sucinta y clara.
Además, la complejidad temporal de algunos algoritmos tiene un mejor, promedio y peor de los casos:
Peor caso: número máximo de ejecuciones para cualquier tamaño de entrada (límite superior)
Caso promedio: número deseado de ejecuciones para cualquier tamaño de entrada
Mejor caso: número mínimo de ejecuciones para cualquier tamaño de entrada (límite inferior)
En la práctica, la preocupación general es la operación del algoritmo en el peor de los casos, por lo que la complejidad temporal de la búsqueda de datos en la matriz es O(N).
2.3 Ejemplo de cálculo de complejidad temporal
2.3.1 Ejemplo 1
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
La operación básica se realiza 2N+10 veces, y la complejidad de tiempo es O(N) al derivar el método de orden O grande.
2.3.2 Ejemplo 2
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
++count;
}
for (int k = 0; k < N; ++k)
{
++count;
}
printf("%d\n", count);
}
La operación básica se realiza M+N veces, hay dos incógnitas M y N, y la complejidad temporal es O(N+M)
Conclusión: La complejidad del tiempo no necesariamente tiene una sola incógnita, sino que puede haber dos, esto depende de las incógnitas específicas del parámetro, pero si el título nos dice:
- M es mucho mayor que N, y la complejidad temporal se convierte en O(M).
- M y N tienen aproximadamente el mismo tamaño, y la complejidad del tiempo se convertirá en O(M) u O(N), los cuales se pueden escribir.
2.3.3 Ejemplo 3
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
}
La operación básica se realiza 100 veces y la complejidad temporal es O(1) al derivar el método de orden O grande
2.3.4 Ejemplo 4
//计算strchr的时间复杂度?
const char* strchr(const char* str, int character);
Aquí hay una implementación aproximada de esta función:
while(*str)
{
if(*str == character)
return str;
else
++str;
}
return NULL;
La operación básica se realiza mejor una vez, la peor es N veces, la complejidad de tiempo es generalmente la peor y la complejidad de tiempo es O (N)
2.3.5 Ejemplo 5
//计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
Nota: El bucle de dos capas no es necesariamente O(N 2 ), sino que también depende de la implementación específica de la función.
Número de primeras comparaciones: N - 1
Número de segundas comparaciones: N - 2
Número de terceras comparaciones: N - 3
···
Número de comparaciones N-1: 1
Peor caso: F(N) = (N*(N-1))/2
Mejor caso: F(N) = N - 1 (comparando la primera ronda, no ocurre ningún intercambio, lo que indica que los datos proporcionados están en orden, por lo que no es necesario continuar con la clasificación)
Complejidad: O(N 2 ) (peor caso)
2.3.6 Ejemplo 6
//计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n;
while (begin < end)
{
int mid = begin + ((end - begin) >> 1);
//用右移运算符是为了防止(end+begin)的值溢出,超出最大整数值
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}
El código anterior utilizabúsqueda binaria。
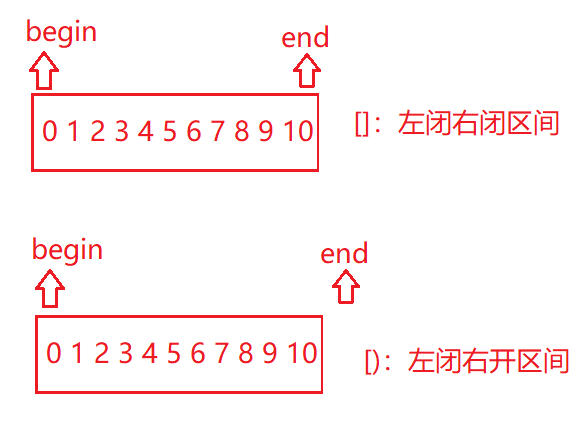
El código anterior es un intervalo cerrado por la izquierda y abierto por la derecha. La diferencia entre los dos métodos de escritura es el procesamiento del límite. No importa qué intervalo sea, debe mantenerse hasta el final . El siguiente es el método de búsqueda binaria código del intervalo cerrado por la izquierda y cerrado por la derecha:
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}
Mejor caso: O(1)
Peor de los casos:
Supongamos que hemos buscado X veces, y finalmente solo queda un elemento, y todavía no lo hemos encontrado, entonces
1 (un elemento restante) * 2 X = N
X = registro 2 N
Complejidad de tiempo: O(log 2 N) (algunos se abrevian como logN , y algunos incluso se abrevian como lgN, pero al final este método de escritura tiene errores y no se recomienda)
Conclusión: para analizar con precisión la idea del algoritmo, no solo mire la cantidad de capas del bucle.
2.3.7 Ejemplo 7
//计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1) * N;
}
A través del análisis computacional, se encuentra que las operaciones básicas se repiten N veces (por supuesto, el número de llamadas a la función es N+1), y la complejidad del tiempo es O(N).
Aquí hay una variación de la función anterior:
long long Fac(size_t N)
{
if (0 == N)
return 1;
for(size_t i = 0;i < N;i++)
{
printf("%d",i);//看这个语句的执行次数
}
return Fac(N - 1) * N;
}
Primera llamada de función: N
Segunda llamada de función: N - 1
···
Llamada de función enésima: 1
Llamada de función N+1: 0 (el bucle for no puede continuar porque N=0)
F(N) = (N + 1) * N / 2
Entonces la complejidad del tiempo es:O(N 2 )
Aviso:
Cálculo de la complejidad del tiempo del algoritmo recursivo:
- Cada llamada de función es O (1), luego depende del número de recursividad
- Cada llamada de función no es O(1), depende de la acumulación del número de llamadas recursivas.
2.3.8 Ejemplo 8
//计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
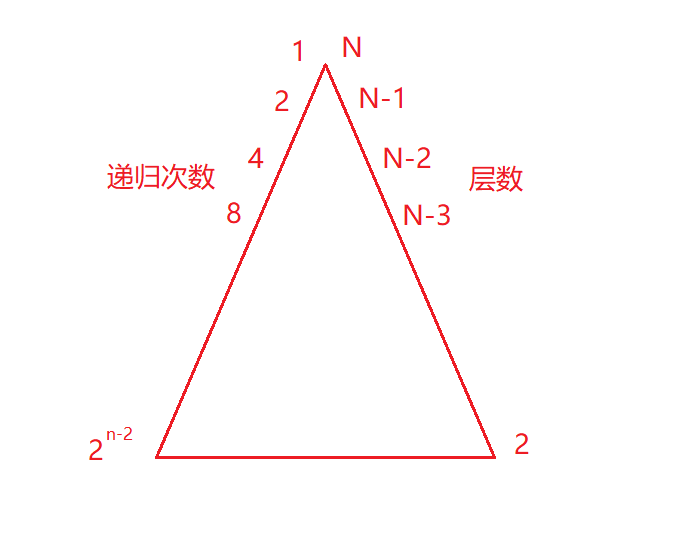
En este punto, puedes usar la fórmula de la serie proporcional para calcular (1*(1 - 2 N-1 ))/(1-2) = 2 N-1 -
1 (en este momento imaginamos una situación completa, pero en hecho ¿Hay algún lugar donde esté lleno, por ejemplo, no hay ningún lugar en la esquina inferior derecha arriba, porque esos números son relativamente pequeños y no pueden llegar allí)A través del análisis computacional, se encuentra que la operación básica se repite 2 N veces (2 N-1 se considera como 2 N de potencia) veces, y la complejidad del tiempo es O (2 N ).
3. Complejidad espacial
La complejidad del espacio también es una expresión matemática, que es una medida de la cantidad de espacio de almacenamiento ocupado temporalmente por un algoritmo durante su funcionamiento.
La complejidad del espacio no es cuántos bytes de espacio ocupa el programa, porque esto no tiene mucho sentido, entonces ** la complejidad del espacio cuenta el número de variables. **
Las reglas de cálculo de la complejidad del espacio son básicamente similares a la complejidad práctica y también utilizan la notación asintótica de O grande.
Nota: El espacio de pila (parámetros de almacenamiento, variables locales, cierta información de registro, etc.) requerido por la función para ejecutarse ha sido determinado durante la compilación, por lo que la complejidad del espacio está determinada principalmente por el espacio adicional solicitado explícitamente por la función en tiempo de ejecución.
3.1 Ejemplo 1:
//计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
Análisis: Se abren un total de tres variables de fin, intercambio e i, es decir, se utiliza una cantidad constante de espacio adicional, por lo que la complejidad del espacio es O(1).
3.2 Ejemplo 2:
//计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
Análisis: un total de (n+1) espacios enteros se abren dinámicamente, por lo que la complejidad del espacio es O(N).
3.3 Ejemplo 3:
//计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
Análisis: la llamada recursiva se realiza N veces y se abren N marcos de pila, y cada marco de pila utiliza una cantidad constante de espacio. La complejidad del espacio es O(N)
3.4 Ejemplo 4
//计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
Nota: El tiempo es acumulativo y el espacio se puede reutilizar.
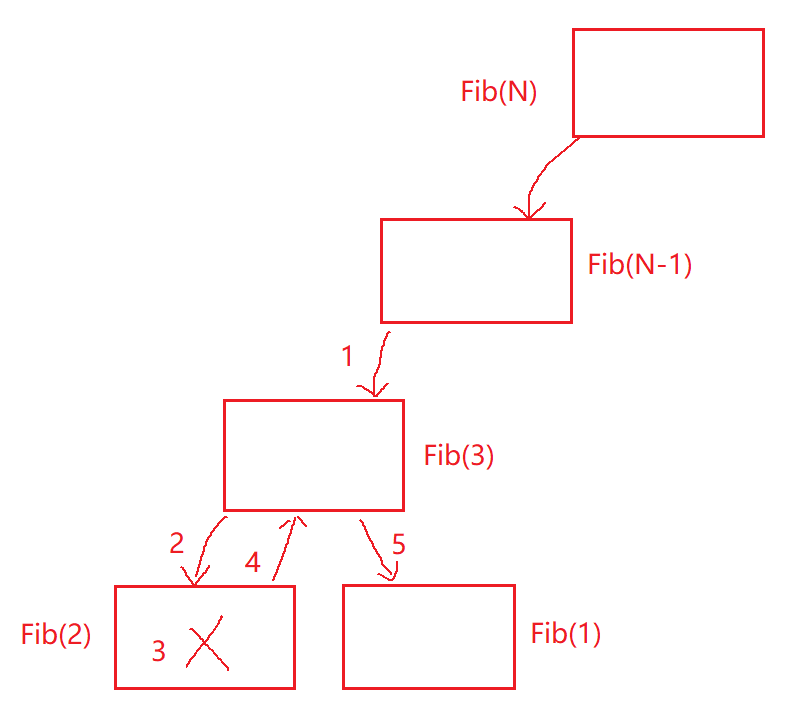
Análisis: Después de llamar a Fib(3), primero llame a Fib(2). Después de llamar a Fib(2), el marco de pila de Fib(2) será destruido. Después de que se destruya el marco de pila de Fib(2), continúe para llamar a Fib(1), el espacio usado por el marco de pila Fib(1) en este momento es el mismo espacio que el espacio usado por el marco de pila Fib(2) justo ahora. El espacio ocupado por los marcos de pila abiertos por la misma capa es el mismo espacio. es decir,En un momento, se abre un total de N-1 marcos de pila, por lo que la complejidad del espacio es O(N).
Por ejemplo:
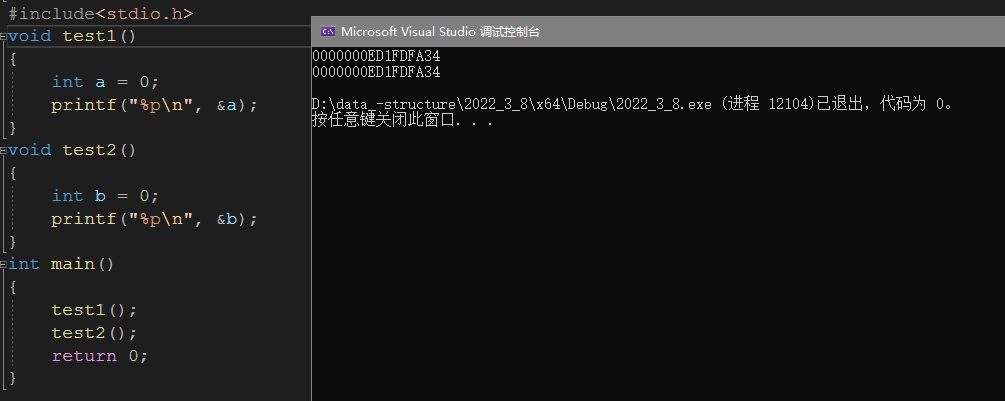
Explicación: después de que se destruye el espacio del marco de pila de f1, f2 sobrescribe el espacio del marco de pila original de f1.(La destrucción del espacio es sólo para devolver el derecho de uso al sistema)
4. Comparación de complejidad común
La complejidad común del algoritmo general es la siguiente:
| 5201314 | O(1) | orden constante |
|---|---|---|
| 3n + 4 | En) | orden lineal |
| 3n 2 + 4*n + 5 | O(n 2 ) | Orden cuadrado |
| 3log 2 n + 4 | O (log 2 n) | logarítmico |
| 2n + 3n log 2 n + 4 | O(nlog 2 n) | nlog 2 enésimo orden |
| n 3 + 2n 2 + 4n + 6 | O(n 3 ) | orden cubico |
| 2 norte | O(2^n) | orden exponencial |
Comparación de complejidad:
O(n!) > O(2 n ) > O(n 2 ) > O(nlog 2 n) > O(n) > O(log 2 n) > O(1)
5. oj ejercicios de complejidad
5.1 Números que desaparecen
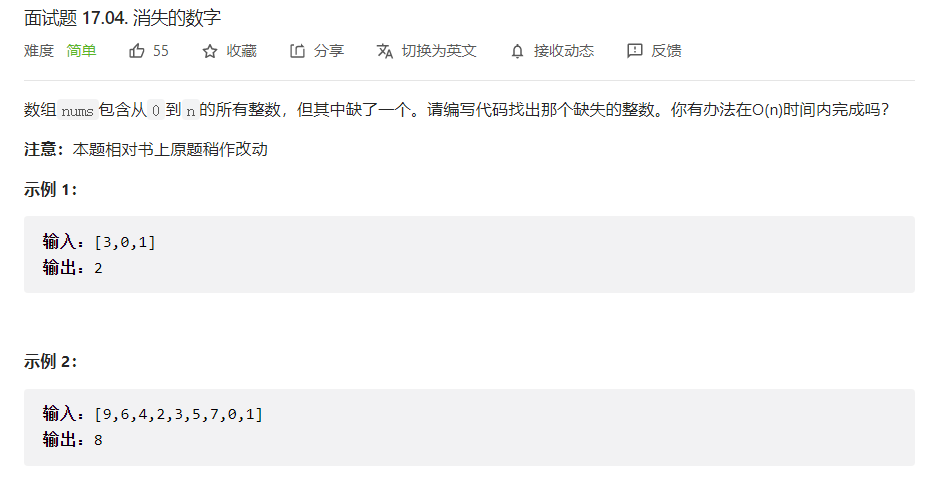
Solución:
sort (burbuja(N 2 ), qsort(nlog 2 N)) (no elegible)
Mapeo (método de subíndices: a cuántos subíndices corresponde cada valor) (O(N)), pero este método tiene una complejidad de espacio O(N)
Visualización de código:
int *ret = (int*)malloc(sizeof(int)*(numsSize+1)); int i = 0; for(i = 0;i<numsSize+1;i++) { ret[i] = -1; } for(i = 0;i<numsSize;i++) { ret[nums[i]] = nums[i]; } for(i = 0;i<numsSize+1;i++) { if(ret[i]==-1) { return i; } } return -1; } ```XOR (use un valor de variable para XOR los datos de 0 a N, y luego XOR con los datos dados) (O(N))
int value = 0; int i = 0; for (i = 0; i <= numsSize; i++) { value ^= i; } for (i = 0; i < numsSize; i++) { value ^= nums[i]; } return value; } ```Fórmula aritmética . Reste todos los datos de la matriz original de la suma de 0~N. (EN))
int sum = 0; int i = 0; int n = numsSize; sum = (n + 1) * n / 2;//等差数列的和的公式 for (i = 0; i < numsSize; i++) { sum -= nums[i]; } return sum; } ```
5.2 Matrices giratorias
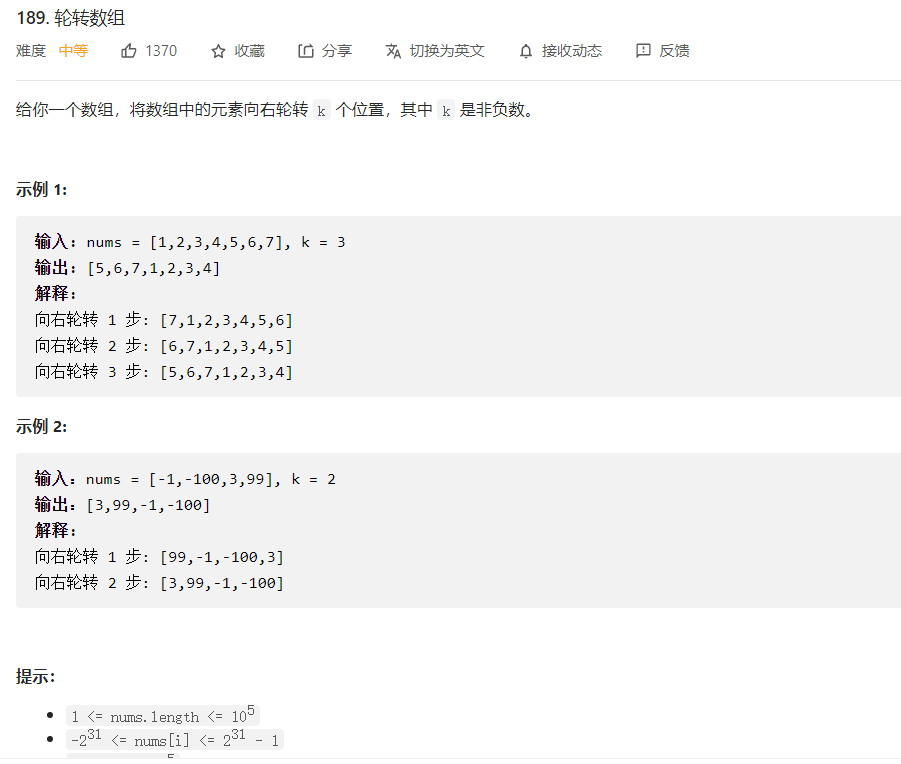
Avanzado:
- Proponga tantas soluciones como sea posible, hay al menos tres formas diferentes de abordar este problema.
- ¿Puedes resolver este problema usando un algoritmo in situ
O(1)con complejidad espacial ?
Gire a la derecha k veces, un carácter a la vez.
complejidad del tiempo:
Último caso: O(N)
Peor caso: O(N*K) (por supuesto, también se puede escribir como O(N 2 )
Complejidad espacial: O(1)
Para abrir una matriz adicional, coloque la última k al frente de la matriz abierta y coloque la primera N - k en la parte posterior de la matriz.
Complejidad de tiempo: O (N) (N recorre elementos de matriz en movimiento)
Complejidad del espacio: O(N)
Tres tiempos de inversión: el primero: se invierten los primeros N - K; el segundo tiempo: se invierten los últimos K; el tercero: se invierte el todo.
Complejidad temporal: O(N) (un total de 2N elementos se invierten)
Complejidad espacial: O(1)
Código:
while(left<=right) { int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; left++; right--; } } void rotate(int* nums, int numsSize, int k){ k%=numsSize; reverse(0,numsSize - k-1,nums); reverse(numsSize - k,numsSize-1,nums); reverse(0,numsSize - 1,nums); } ```