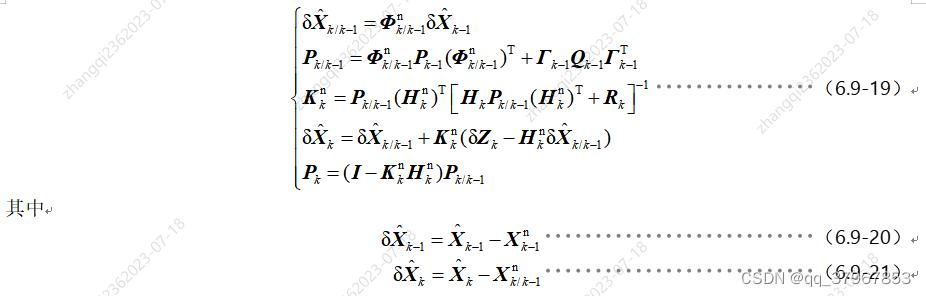1. Derivación de Kalman:
1) Primero observe el modelo de espacio de estado del sistema estocástico del sistema: (lineal)
El llamado lineal significa que la recursión o ecuación de transición de estado es lineal.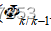 
En cuanto a la explicación de los parámetros, lea el libro usted mismo.
2) El valor en el tiempo k-1 menos la estimación del estado óptimo en el tiempo k-1 = error de estimación del estado en el tiempo k-1. Primero calcule el error de estimación del estado en el momento k-1 ( la desviación entre el valor de referencia y el valor estimado ):
3) De acuerdo con la estimación del estado óptimo en el momento k-1 y la ecuación de estado del sistema, el estado en el momento k (valor actual tiempo) se puede estimar de manera óptima (pronóstico óptimo de un paso):
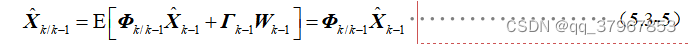
4) Calcular el error de pronóstico de un paso del estado es:
5) Poner 1) y 3) en 4) y combinar 2) para obtener:
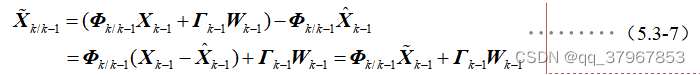
ahora el pronóstico de un paso del estado se calcula el error de pronóstico, luego se puede calcular el estado Predicción de un paso de la matriz de error cuadrático medio:
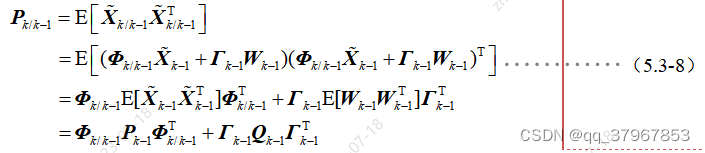
mientras que la matriz de error de estimación del estado en el tiempo k-1 es:
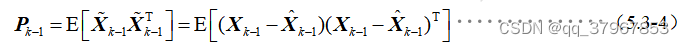
Calcule y mida de la misma manera:
1) A través de la matriz de error de un paso predicción del estado y la ecuación de medición del sistema, se puede hacer una predicción de un paso de la medición en el tiempo:
2) Medición La fórmula para el error de pronóstico de un paso es:
3) Traiga la fórmula del sistema y 1) la fórmula a 2) obtener el error de pronóstico de un paso de medición
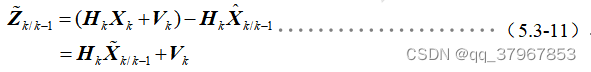: 4) Calcular la matriz de error cuadrático medio del pronóstico de un paso de medición, el pronóstico de un paso de estado y el pronóstico de un paso de medición Matriz de error cuadrático medio: Hasta ahora
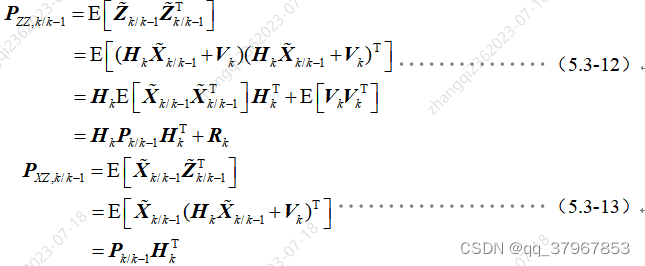
, es posible usar la predicción de un paso de la ecuación de estado del sistema para estimar el valor en el momento actual, pero como no se usa información de la ecuación de medición, la precisión de la estimación no será alta. Y debido a que el error de predicción de un paso de la medición contiene la información de la predicción de un paso del estado, por lo tanto, considerando la consideración integral, la estimación del estado actual se corrige por el error de predicción de un paso de la medición como la estimación del estado óptimo final:
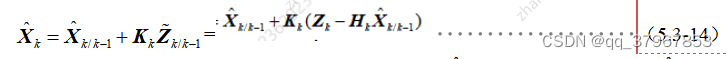
5) Simplifique la fórmula anterior:
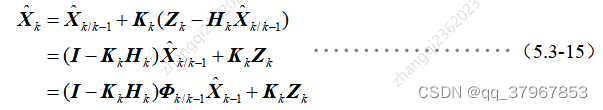
Se puede ver que la estimación del estado actual es una combinación lineal (estimación ponderada) de la estimación del estado en el momento anterior y la medición actual, y la estimación anterior se corrige por el error de medición para obtener el estimación posterior.
A continuación, calcule K para minimizar el error de estimación posterior (el error de estimación de estado en el momento actual):
6) El error de estimación de estado en el momento actual k es:
7) Coloque la fórmula anterior 5) en 6) para obtener:
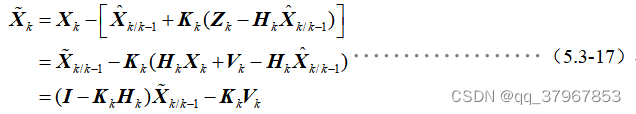
8) Encuentre el momento k de la misma manera (Momento actual) La matriz de error cuadrático medio de la estimación del estado:
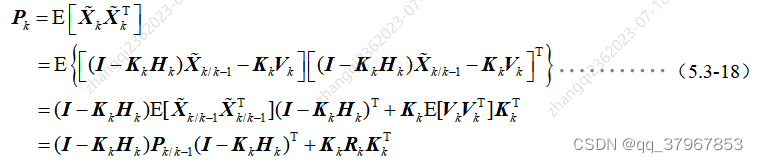
9) El error de estimación es un vector aleatorio, y el significado de "minimizar el error" se estipula para minimizar la suma de la media errores cuadráticos de cada componente , lo que
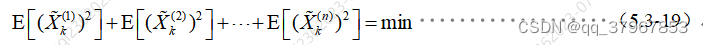
equivale a:
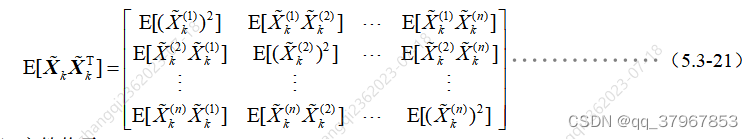
10) Porque la matriz de error cuadrático medio debe ser una matriz simétrica , por lo que la fórmula 8) se puede expandir como:
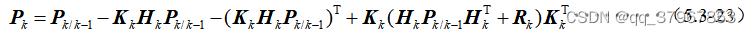
11) Encuentre simultáneamente la operación de seguimiento en ambos lados
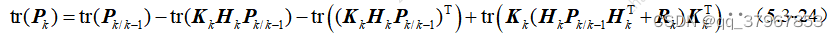
de la fórmula 10) , y obtenemos: la fórmula anterior es una función cuadrática sobre la matriz de parámetros indeterminada K, por lo que tr§ debe tener un valor de polo (según el significado de probabilidad, debería ser un valor mínimo aquí).
Para facilitar el uso del método de derivación para obtener el extremo de la fórmula anterior, se introducen dos ecuaciones para derivar la matriz a partir de la traza de la matriz cuadrada, que son las siguientes: Derivación de K en ambos lados al mismo
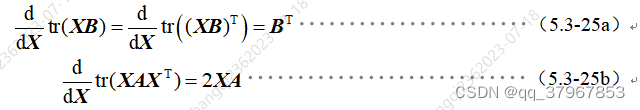
tiempo :
Según el valor extremo de la función, se obtiene:
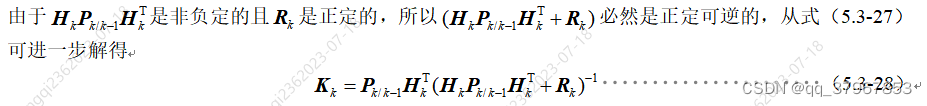
es decir, cuando K Cuando es igual a los valores anteriores, el error de estimación del estado actual es el más pequeño. En este punto, lleve la fórmula anterior a 10) para obtener la matriz de error cuadrático medio en el tiempo k:
Hasta ahora, se deducen cinco fórmulas de filtrado de Kalman:
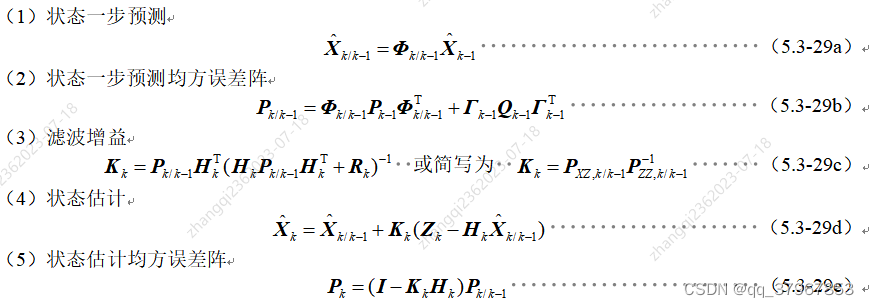
2. Derivación extendida de Kalman:
1) Primero observe el modelo de espacio de estado del sistema estocástico del sistema: (no lineal)
La única diferencia con Kalman es que el Kalman extendido trata con modelos no lineales, por lo que se requiere una expansión de Taylor para la ecuación de transición de estado (independientemente de la predicción o medición ) Obtenga la matriz jacobiana para la linealización.
1) Calcular la estimación del estado en el tiempo k-1 de la misma manera:
2) De acuerdo con la estimación del estado óptimo en el tiempo k-1 y la ecuación de estado del sistema, el estado en el tiempo k (momento actual) se puede estimar de manera óptima (momento óptimo). predicción de un paso): 3
) El error de predicción de un paso del estado de cálculo es:
En la derivación de Kalman, este paso se lleva directamente a la ecuación del sistema, pero aquí primero debe linealizarse: De la misma
manera, el medición:
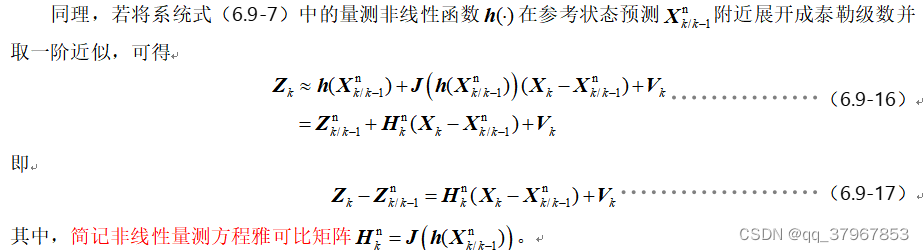
Por lo tanto, el sistema no lineal original se puede reescribir como un sistema lineal:
Reescribir 5 fórmulas:
