第三题

因为 H_1 和 H_2 是群 G 的正规子群,所以
对 于 ∀ g ∈ G 和 ∀ h 1 ∈ H 1 , ∀ h 2 ∈ H 2 对于 ∀g∈G 和 ∀h_1∈H_1, ∀h_2∈H_2 对于∀g∈G和∀h1∈H1,∀h2∈H2
∃ h 1 ′ 使 得 g h 1 = h 1 ′ g , ∃ h 2 ′ 使 得 g h 2 = h 2 ′ g ∃ h_1^{'} 使得 gh_1=h_1^{'}g,∃ h_2^{'} 使得 gh_2=h_2^{'}g ∃h1′使得gh1=h1′g,∃h2′使得gh2=h2′g
所 以 对 于 ∀ h 1 ∈ H 1 , ∀ h 2 ∈ H 2 , ∃ h 1 ′ ∈ H 1 , ∃ h 2 ′ ∈ H 2 所以对于∀h_1∈H_1,∀h_2∈H_2,∃h_1^{'}∈H_1,∃h_2^{'}∈H_2 所以对于∀h1∈H1,∀h2∈H2,∃h1′∈H1,∃h2′∈H2
使 得 g h 1 h 2 = h 1 ′ g h 2 = h 1 ′ h 2 ′ g , 即 g H 1 H 2 ⊂ H 1 H 2 g ① 使得gh_1h_2=h_1^{'}gh_2=h_1^{'}h_2^{'}g,即gH_1H_2⊂H_1H_2g① 使得gh1h2=h1′gh2=h1′h2′g,即gH1H2⊂H1H2g①
同 理 对 于 ∀ h 1 ′ ∈ H 1 , ∀ h 2 ′ ∈ H 2 , ∃ h 1 ∈ H 1 , ∃ h 2 ∈ H 2 同理对于∀h_1^{'}∈H_1,∀h_2^{'}∈H_2,∃h_1∈H_1,∃h_2∈H_2 同理对于∀h1′∈H1,∀h2′∈H2,∃h1∈H1,∃h2∈H2
使 得 h 1 ′ h 2 ′ g = h 1 ′ g h 2 = g h 1 h 2 , 即 H 1 H 2 g ⊂ g H 1 H 2 ② 使得h_1^{'}h_2^{'}g=h_1^{'}gh_2=gh_1h_2,即H_1H_2g⊂gH_1H_2② 使得h1′h2′g=h1′gh2=gh1h2,即H1H2g⊂gH1H2②
由①和②可得 gH_1H_2 = H_1H_2g,即 H_1H_2 是群G的正规子群
第五题

充分性:
因为 G 是阿贝尔群,所以对于 ∀a,b∈G,a·b=b·a
所 以 ϕ ( a ⋅ b ) = ( a b ) 2 = a b ⋅ a b = a 2 b 2 = ϕ ( a ) ϕ ( b ) 所以ϕ(a⋅b)=(ab)^2=ab⋅ab=a^2b^2=ϕ(a)ϕ(b) 所以ϕ(a⋅b)=(ab)2=ab⋅ab=a2b2=ϕ(a)ϕ(b)
所以 ϕ 是一种群同态
必要性:
因为 ϕ 是一种群同态,所以对于 ∀a,b∈G,
有 ϕ ( a ⋅ b ) = ( a b ) 2 = ϕ ( a ) ϕ ( b ) = a 2 b 2 有ϕ(a⋅b)=(ab)^2=ϕ(a)ϕ(b)=a^2b^2 有ϕ(a⋅b)=(ab)2=ϕ(a)ϕ(b)=a2b2
即 a b ⋅ a b = a 2 ⋅ b 2 即ab·ab=a^2·b^2 即ab⋅ab=a2⋅b2
通过消去律可得
b ⋅ a = a ⋅ b b·a=a·b b⋅a=a⋅b
所以 G 是阿贝尔群
第七题
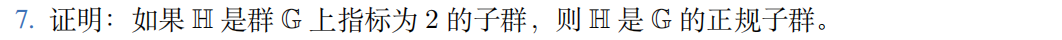
[G : H] = 2, 所以存在 g 使得 G 被划分为 H 与 gH.
而当 g ∈ H 时, gH = Hg = H
当 g ∉ H 时, gH != H, Hg != H, 则 gH = Hg 都在另一个划分上, 即 H 是 G 的正规子群
第九题
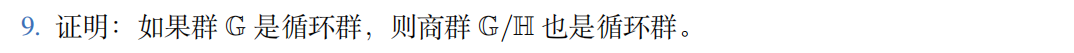
设 G 的生成元为 g, 现取 ∀g_1,g_2∈G, 则必 ∃g_3∈G, 有 g_3 = g_1g_2
H 为 G 的子群,所以 H 也为循环群
对于 G/H 有 g_1Hg_2H = g_3H ∈ G
即 g_3H 也是 G 的子群,即 G/H 也是循环群