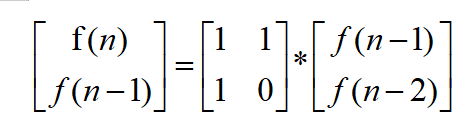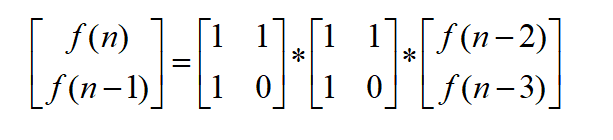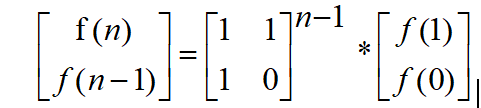Speaking of the reason for the rapid power learning of the matrix, it feels relatively low. It comes from the learning of the recursive algorithm of the Fibonacci sequence. I personally think that when the amount of data is small, recursion is a good choice.
First, briefly introduce the common recursive algorithm:
The following is using the classic recursive algorithm
#include<iostream>
using namespace std;
int Fbi(int i)
{
if (i<2)
{
return i==0 ? 0:1;
}
return Fbi(i-1)+Fbi(i-2);
}
int main()
{
int n;
cin>>n;
cout<<Fbi(n)<<endl;
return 0;
}
Let's briefly analyze the time complexity of our direct and violent use of recursion to solve the Fibonacci sequence to
solve F(n), we must first calculate F(i-1) and F(i-2), and calculate F(i-1) And F(i-2), F(i-3) and F(i-4) must be calculated first. . . . . . And so on, until you have to calculate F(1) and F(0) first, and then inversely get the results of F(n-1) and F(n-2), so as to get F(n) to calculate many repeated values , Causing a lot of waste in time, the time complexity of the algorithm increases exponentially with the increase of N, the time complexity is O(2^n), that
is, does the n-th power of 2 feel very bad? Yeah!
So this algorithm is definitely not advisable in the case of big data. Let's make a simple optimization of this algorithm.
Optimize it: matrix fast power algorithm
Let’s take a small look at the recurrence of the Fibonacci function.
f(n)=f(n-1)+f(n-2)
If we add f(n-1) to both sides at the same time,
f(n)+f(n-1)=f(n-1)+f(n-1)+f(n-2)
we can simply perform matrix multiplication to change the original formula into the down formula.
Simple multiplication. I won’t introduce the rules here. If you don’t have a basic knowledge of linear algebra, you can go to MOOC and simply learn it.
Let’s perform a simple recursion on the above formula
... and finally get the result
. Then we will use Fibo The expression of the matrix multiplication of the sequence of numbers is written,
and then we can find the law in the matrix multiplication, and we can find the law
simply by using the code.
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=1e9+9;
const int N=2;
ll tmp[N][N],res[N][N];
void multi(ll a[][N],ll b[][N],int n)
{
memset(tmp,0,sizeof(tmp));
for(ll i=0;i<n;i++)
{
for(ll j=0;j<n;j++)
{
for(ll k=0;k<n;k++)
{
tmp[i][j]+=(a[i][k]*b[k][j])%mod;
}
tmp[i][j]=tmp[i][j]%mod;
}
}
for(ll i=0;i<n;i++)
for(ll j=0;j<n;j++)
a[i][j]=tmp[i][j];
}
void Pow(ll a[][N],ll m,int n)
{
memset(res,0,sizeof(res));
for(ll i=0;i<n;i++) res[i][i]=1;
while(m)
{
if(m&1)
multi(res,a,n);
multi(a,a,n);
m>>=1;
}
}
int main()
{
ll m;
int n;
ll a[N][N];
while(~scanf("%lld",&m))
{
n=2;
a[0][0]=1,a[0][1]=1,a[1][0]=1,a[1][1]=0;
Pow(a,m,n);
cout<<res[1][0];
}
cout<<endl;
return 0;
}
Although the code looks more complicated, if we simply perform a wave of time complexity analysis
, we will find that we have reduced the algorithm complexity to the log level, which greatly reduces the time of simple recursive algorithms in large numbers. the complexity.
Okay, next time I will share other applications of matrix fast power.