On the fast power matrix

Fast power matrix

One. Brief introduction

First, power is fast matrix algorithm extended from the power of fast, the need for rapid power and the knowledge of linear algebra. Fast power is related to the binary nature quickly calculate X ⁿ , Mi is the matrix by rapid recurrence of formula into a matrix, the result of solving a recursive process into solving a matrix of n -th power of the process, so that it can with the power to speed up the fast recursive solver.

For example, we use Fibonacci column to explain the specific power of fast flow matrix. Everyone knows recursion formula F. (N-) = F. (. 1-n-) F. + (2-n-) . This formula is very easy to understand, but for solving becomes very slow and when larger items, so we can consider the use of fast power matrix to optimize the math process. In general, we want to get a recurrence relationship between the matrix obtained by recursive formula of the form T * A (n-1) = A (n) ( wherein T , A (n--. 1) , A (n- ) are matrix ) .

For F (the n-) , we can get a recurrence relation between the matrix is

Among them, it should be noted that, in order to facilitate operations, we construct the matrix are square, where A _{the n-} actually a phalanx 2 * 2, but we are only interested in A _{the n-} left, so there is no written A _{the n-} right. Obviously, the equation given above is true, then, we ask if F (n), can be determined to A (n-) = T ^n-2- * A (. 1),

A (1) is a 2 * 2 matrix to the left two 1, the value F (n) is A (n) At this point the top left corner. In this way, we put a recursive computation process optimization, and then use the power of extremely rapid fast matrix solver.

Fast power matrix of the difficulty lies in the structure of the matrix.

Here a simple recursive formula
1.f (n-) = A * F (. 1-n-) F + B * (n--2) + C; (A, B, C is a constant)

 

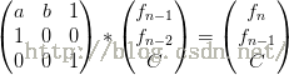
2.f (n) = c ^ nf (n-1); (c is a constant)

two. Code

const int N = 2;
const int mod = 10000;
struct Matrix
{
    int mat[N][N];
    Matrix(){};
    Matrix operator*(Matrix const &b) const
    {
        Matrix res;
        memset(res.mat,0,sizeof(res.mat));
        for(int i = 0;i<N;++i)
        {
            for(int j = 0;j<N;++j)
            {
                for(int k = 0;k<N;++k)
                {
                    printf("%d %d %d\n",i,j,k);
                    res.mat[i][j] = (res.mat[i][j]+this->mat[i][k]*b.mat[k][j])%mod;
                }
            }
        }
        return res;
    }
    void Print()
    {
        for(int i =0;i<N;++i)
        {
            for(int j = 0;j<N;++j)
                printf("%d ",mat[i][j]);
            printf("\n");
        }
        return ;
    }
};
Matrix pow_mod(Matrix base,int n)
{
    Matrix res;
    memset(res.mat,0,sizeof(res.mat));
    for(int i = 0;i<N;++i)
        res.mat[i][i] = 1;
    while(n>0)
    {
        if(n&1)
        {
            res.Print();
            res= res*base;
        }
        base = base*base;
        n>>=1;
        res.Print();
    }
    return res;

}

three. Related exercises