机器学习（优化算法三）——坐标轴下降

概述

Lasso回归采用的是坐标轴下降法(Coordinate Descent， CD)是一种迭代法，通过启发式的方法一步步的迭代求解函数的最小值，和梯度下降法(GD)不同的是，坐标轴下降法是沿着坐标轴的方向去下降，而不是采用梯度的负方向下降。

示意图大致如下：

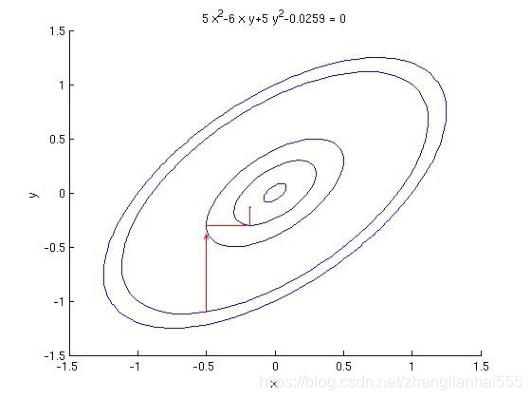
坐标轴下降法利用EM算法的思想，在参数更新过程中，每次均先固定 m-1 个参数值，求解剩下的一个参数的局部最优解；然后进行迭代式的更新操作。

坐标轴下降法的核心思想是多变量函数 $F(X)$ 可以通过每次沿着一个方向优化来获取最小值；其数学依据是：对于一个可微凸函数f(θ)，其中θ为n*1的向量，如果对于一个解 $θ=(θ_1 ,θ_2 ,...,θ_n )$，使得 $f(θ)$ 在每一个坐标轴 $θ_i (i=1,2,..,n)$ 上都能达到最小值，则 $θ=(θ_1 ,θ_2 ,...,θ_n)$ 就是的 $f(θ)$ 全局的最小值点。

在坐标轴下降法中，优化方向从算法的一开始就固定了，即沿着坐标的方向进行变化。在算法中，循环最小化各个坐标方向的目标函数。即：如果 $x^k$ 给定，那么 $x^{k+1}$ 的第i维度为:
$X_i^{k+1} = \argmin\limits_{y\in R} f \left( x_1^{k+1},..., x_{i-1}^{k+1},y, x_{i+1}^k,...,x_n^k \right)$
因此，从一个初始的 $x_0$ 求得函数 $F(X)$ 的局部最优解，可以迭代获取 $x_0、x_1、x_2...$的序列，从而可以得到:
$F(X^0) \geq F(X^1) \geq F(X^2) \geq ...$

算法过程

1. 给 θ 向量随机选取一个初值，记做 $θ_0$ ；

2. 对于第 k 轮的迭代，从 $θ_1^k$ 开始计算， $θ_n^k$ 到为止，计算公式如下：
   $\begin{aligned} \theta_1^k \,\,\,\ &= \,\,\,\, \argmin \limits_{\theta_1} J \left( \theta _1,\theta_2^{k-1},\theta_3^{k-1},...,\theta_n^{k-1}\right) \\ \theta_2^k \,\,\,\ &= \,\,\,\, \argmin \limits_{\theta_2} J \left( \theta _1^k,\theta_2,\theta_3^{k-1},...,\theta_n^{k-1}\right) \\......\\ \theta_n^k \,\,\,\ &= \,\,\,\, \argmin \limits_{\theta_n} J \left( \theta _1^k,\theta_2^k,\theta_3^k,...,\theta_n \right) \end{aligned}$

   检查 $θ_k$ 和 $θ_{k−1}$ 向量在各个维度上的变化情况，如果所有维度的变化情况都比较小的话，那么认为结束迭代，否则继续 k+1 轮的迭代。

备注：在求解每个参数局部最优解的时候可以求导的方式来求解。

坐标轴下降法和梯度下降法的区别

坐标轴下降法在每次迭代中，计算当前点处沿一个坐标方向进行一维搜索 ，固定其它维度的坐标方向，找到一个函数的局部极小值。而梯度下降总是沿着梯度的负方向求函数的局部最小值；

坐标轴下降优化方法是一种非梯度优化算法。在整个过程中依次循环使用不同的坐标方向进行迭代，一个周期的一维搜索迭代过程相当于一个梯度下降的迭代；

梯度下降是利用目标函数的导数来确定搜索方向的，该梯度方向可能不与任何坐标轴平行。而坐标轴下降法法是利用当前坐标方向进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值；
两者都是迭代算法，且每一轮迭代都需要O(mn)的计算量(m为样本数，n为维度数)