1、概述
在机器人研究中,我们希望机器人能够按照我们的预想在空间中运动,这自然就需要表达机器人部件或其机构本身的位置和姿态。为了定义和运用表达位姿的数学量,我们必须定义坐标系并给出其表达规则。
我们既定有这样一个体系,即存在一个世界坐标系,我们定义的位姿都是参照这个世界坐标系或者由世界坐标系定义的笛卡尔坐标系。
2、位置、姿态
如何定量描述机器人的位姿。注意这里“位姿”,包含了位置和姿态。我们一个一个来看。
2.1 位置
如果我们的机器人可以看做是在平面内运动,那么可以用两个坐标来描述它的位置:
A=[x,y]T

相应的,如果它在三维空间中,我们就可以用三个空间坐标来表示,如下图中,我们可以这样表达
:AP=[x,y,z]T

2.2 姿态
姿态的表达比点的位置要复杂。二维情况下,其姿态可以只用一个旋转角
θ表达。三维情况下,姿态的表达方式则有多种。常见的如欧拉角、四元数、旋转矩阵等。
有了位置和姿态,我们就可以描述一个坐标系。进一步,还能描述坐标系间的变换关系。常见的问题如:我们知道世界坐标中的某个点,但是我们需要求这个点相对于机器人的位置,这时,就需要先得到机器人坐标系相对于世界坐标系的坐标值,再根据机器人位姿转换到机器人坐标系中。
2.2.1 二维姿态
二维情况下,其姿态可以只用一个旋转角
θ表达。首先要明确旋转在二维中是绕着某一个点进行旋转,三维中是绕着某一个轴进行旋转。二维旋转中最简单的场景是绕着坐标原点进行的旋转,如下图所示:
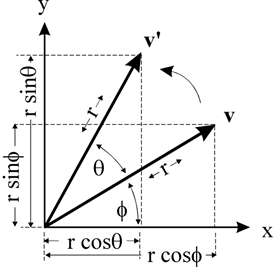
如上图
v 绕 原点旋转θ °,到达
v′,假设
v的坐标是(x, y) ,那么可以推导出
v′点的坐标(x’, y’)(设v的长度为r,与x轴的夹角为
ϕ )
那么根据几何关系我们能够得到:
x=rcosϕy=rsinϕ
x′=rcos(θ+ϕ)y′=rsin(θ+ϕ)
对下面两条进行三角函数展开我们可以得到:
x′=rcosθcosϕ−rsinθsinϕy′=rsinθcosϕ+rcosθsinϕ
对以上式子进行整合最终得出:
x′=xcosθ−ysinθy′=xsinθ+ycosθ
写成矩阵形式:
[x′y′]=[cosθsinθ−sinθcosθ][xy]
2.2.2 三维姿态
我们以下图为例进行说明
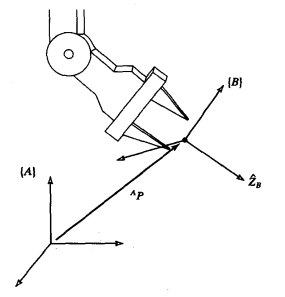
用
XB,YB,ZB表示坐标系{B}主轴方向的单位矢量,在坐标系{A}下,他们写成
AXB,AYB,AZB,将这三个单位矢量按xyz的顺序组成一个
3×3的矩阵,我们成为旋转矩阵,并且这个旋转矩阵是{B}相对于{A}的表达,用
BAR表示:
BAR=[AXB,AYBAZB]=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤
根据上述定义,旋转矩阵的各列的模均为1,且单位矢量相互正交,因此可得:
BAR=ABR−1=ABRT
所以,
BAR的列是{B}的单位矢量在{A}中的描述,而
BAR的行则是{A}的单位矢量在{B}中的描述。
2.3 坐标系的变换
2.3.1 平移变换

在上图中,{A}与{B}具有相同的姿态。我们用矢量
BP表示点P在坐标系{B}的位置。当我们希望以坐标系{A}来表达这些点时,该怎么办呢?
我们先来分析,{B}不同于{A}的只有平移量,可用
APBORG表示{B}的原点相对于{A}的位置。而因为姿态相同,我们可以用矢量相加的方法求点P相对{A}的位置
AP:
AP=BP+APBORG
2.3.2 旋转变换
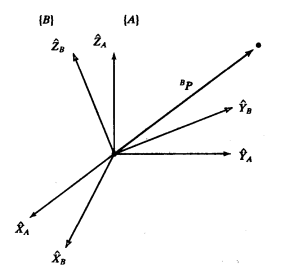
如图,{B}相对于{A}的姿态描述是已知的,而根据上述,三维情况下,旋转可由旋转矩阵表达,因此:
AP=BAR∗BP
2.3.3 一般坐标系的变换
现在考虑一般情况,坐标系{B}的原点与{A}不重合,并且有一个旋转量,{B}原点用矢量
APBORG表示, 同时旋转用
BAR表示,已知
BP,求
AP.

首先将
BP变换到一个中间坐标系,该坐标系与{A}具有相同的姿态,原点和{B}重合,然后用矢量加法将原点平移,得到:
AP=BAR∗BP+APBORG







