简单的说一说SVM--适合仅仅是想了解一下SVM的读者

如果您仅仅看了本文的文字部分，不看推荐的连接，那么您将有以下收获：
1，学会了SVM的英文全称；
2，了解了SVM大概是要干啥，至于如何去做，您依然一无所知；
3，知道如果想要深入学习SVM，要去哪里学习（连接不多，就是怕有人会选择障碍）

本文拟介绍这么几个点：

1SVM算法的基本原理
2拉格朗日乘子和KKT条件
3线性可分SVM算法
4软间隔SVM算法
5非线性可分SVM算法
6核函数
7SMO算法
8SVR回归算法

1SVM算法的基本原理
首先我们说一说啥是SVM？
一看到SVM，我们的直观感觉就是，我擦，深奥。这是个英文缩写吧，他的全称是Support Vector Machine，翻译过来就是支持向量机。看完全称和翻译，一脸懵逼。既然我们这篇文章就是想简单的说一说SVM，那就没必要搞这些有的没的。直接告诉我SVM是干啥的不就完了嘛！

支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度，Accuracy）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力。
上面这段介绍是经常被各类学术论文引用的对SVM的介绍，很显然，这种非人类语言不适合我们这些吃瓜群众，那么到底啥是SVM呢？简单的说法就是：一种分类算法！

小样本并不是说样本的绝对数量少（实际上，对任何算法来说，更多的样本几乎总是能带来更好的效果），而是说与问题的复杂度比起来，SVM算法要求的样本数是相对比较少的。

非线性是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也有人叫惩罚变量）和核函数技术来实现，这一部分是SVM的精髓。

高维模式识别是指样本维数很高，例如文本的向量表示，如果没有经过另一系列文章（《文本分类入门》）中提到过的降维处理，出现几万维的情况很正常，其他算法基本就没有能力应付了，SVM却可以，主要是因为SVM 产生的分类器很简洁，用到的样本信息很少（仅仅用到那些称之为“支持向量”的样本，此为后话），使得即使样本维数很高，也不会给存储和计算带来大麻烦（相对照而言，kNN算法在分类时就要用到所有样本，样本数巨大，每个样本维数再一高，这日子就没法过了……）。

关于SVM介绍大家可以参考这篇系列文章，免票进入

2拉格朗日乘子和KKT条件
看到这个小标题，很多人可能又会懵逼了，SVM和拉格朗日乘子有个锤子关系。。。别急，我们慢慢道来。
开始我们说了，SVM其实就是做分类的算法。既然是算法，就会有一个判断标准，你是分的好还是分的差。我们通常的做法是什么样的呢？我们通常会将利用SVM算法模型得到的结果和真实结果（尽管我们一般没有绝对真实的结果）进行一个比较，差值越小，说明模型越好。说白了，我们相当于对这个差值（也可以叫损失函数）求最小值。
求极值，相信看这个文章的人都会，导数为零嘛，这有啥呢。但是我们常常会遇到这样一种情况，我们有一个待求解的函数，同时这个函数的参数又附加了一些约束条件。很显然，我们无法再简单的对函数求导来获得极值点了。这个时候怎么办呢？两个办法，第一个，我们把条件函数换算成无条件的函数，然后求导。可是问题又来了，很多时候我们无法把条件函数换成无条件函数，那又该咋整呢？
这个时候我们的拉格朗日乘子就可以闪亮登场了。具体做法简单总结就是：引入一个变量，与条件函数相乘并带入带求解函数中形成一个新的函数，求解其中变量的偏导数，并使之为零，再与条件方程联合求解，最终得到极值点。

什么又是KKT条件呢？
网上关于这个的解释也很多，这里介绍无非又是搬弄其他人总结的说法，为了不造成遗漏和误解，这里奉上相关的解释连接，感兴趣的同学可以移步一看KKT的条件

3线性可分SVM算法
首先我们先认识一下何为线性函数？
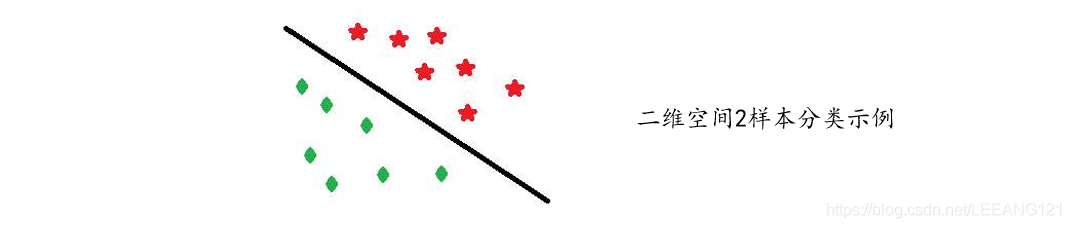
在一维空间里就是一个点，在二维空间里就是一条直线，三维空间里就是一个平面，可以如此想象下去，如果不关注空间的维数，这种线性函数还有一个统一的名称——超平面（Hyper Plane）！

上图是一个二维空间中的二分类问题。实际上很容易看出来，中间那条分界线并不是唯一的，我们把它稍微旋转一下，只要不把两类数据分错，仍然可以达到上面说的效果，稍微平移一下，也可以。此时就牵涉到一个问题，对同一个问题存在多个分类函数的时候，哪一个函数更好呢？显然必须要先找一个指标来量化“好”的程度，通常使用的都是叫做“分类间隔”的指标。
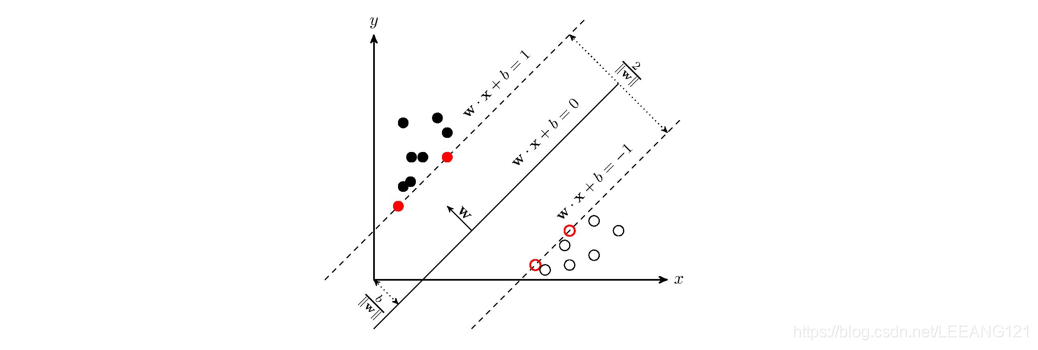
当我们在解决多维空间问题时，我们又会把分类间隔称作几何间隔。几何间隔所表示的正是点到超平面的欧氏距离，我们下面就简称几何间隔为“距离”。以上是单个点到某个超平面的距离（就是间隔，后面不再区别这两个词）定义，同样可以定义一个点的集合（就是一组样本）到某个超平面的距离为此集合中离超平面最近的点的距离。

上图中，中间的实线是分类面，两侧虚线到实线的距离就是几何间隔。显然，最大化几何间隔就是我们的训练目标。

4软间隔SVM算法
我们上面讨论的问题中，我们一直假定训练样本在样本空间或特征空间是线性可分的，即存在一个超平面能将不同类的样本完全划分开，然而，在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；退一步说，即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难判定这个貌似线性可分的结果不是由于过拟合造成的。

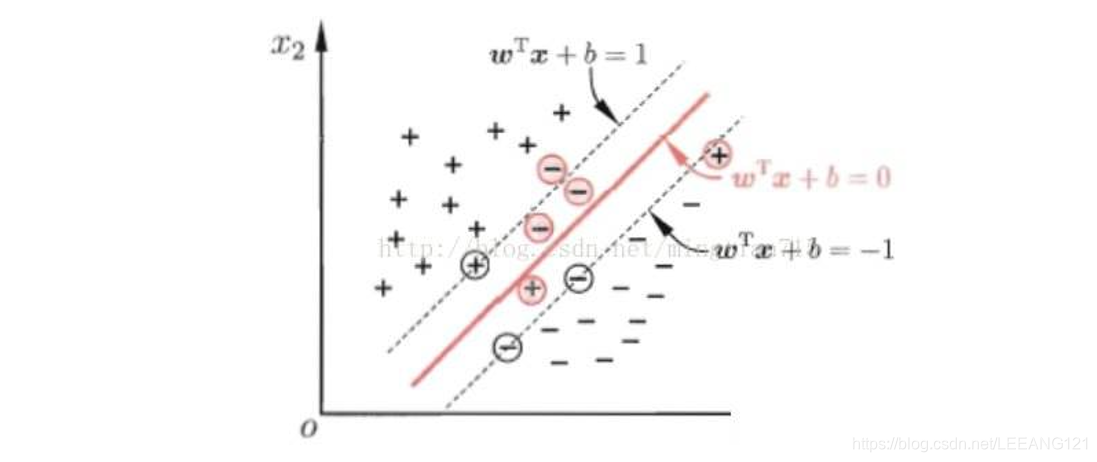
缓解这个问题的一个办法就是允许支持向量机在一些样本上出错，为此引入了‘软间隔’（soft margin）的概念。（下图来自百度）

上图为软间隔示意图，红色圈出了不满足约束的样本。
这是一篇不错的关于SVM的博文，值得收藏传送门

5非线性可分SVM算法
这里主要可以参考这篇文章

6核函数
事实上，大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。在上文中，我们已经了解到了SVM处理线性可分的情况，那对于非线性的数据SVM咋处理呢？对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。

具体来说，在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。

核函数的主要作用之一就是将低维数据映射到高维数据。

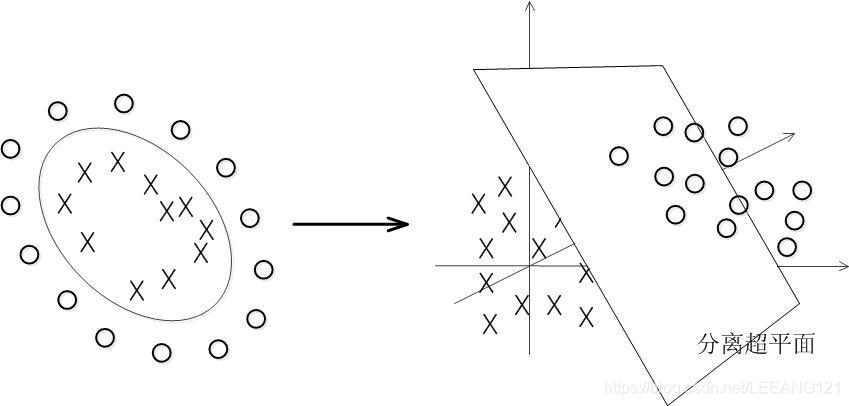
实现方式：

上图所述的这个数据集，我们可以假定是用两个半径不同的圆圈加上了少量的噪音生成得到的（虽然里面那个不太圆），所以，一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。如果用 $X_{1}$和 $X_{2}$来表示这个二维平面的两个坐标的话，我们知道一条二次曲线（圆圈是二次曲线的一种特殊情况）的方程可以写作这样的形式：

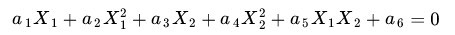
注意上面的形式，如果我们构造另外一个五维的空间，其中五个坐标的值分别为 $Z_{1}=X_{1}$, $Z_{2}=X^{2}_{1}$, $Z_{3}=X_{2}$, $Z_{4}=X^{2}_{2}$, $Z_{5}=X_{1}X_{2}$.那么显然，上面的方程在新的坐标系下可以写作：

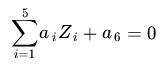
关于新的坐标 $Z$，这正是一个 hyper plane 的方程！也就是说，如果我们做一个映射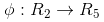 ，将 $X$按照上面的规则映射为 $Z$，那么在新的空间中原来的数据将变成线性可分的，从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。

7SMO算法
关于SMO算法推到的一篇文章

8SVR回归算法
SVR回归，就是找到一个回归平面，让一个集合的所有数据到该平面的距离最近。
SVR是支持向量回归(support vector regression)的英文缩写，是支持向量机(SVM)的重要的应用分支。