https://blog.csdn.net/charlee44/article/details/98474589
https://blog.csdn.net/u011294404/article/details/53605873
https://blog.csdn.net/charlee44/article/details/103443618
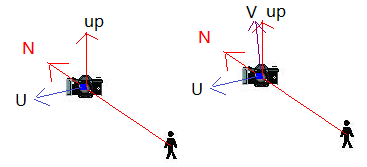
由前文得知,视图变换构建了一个视空间/摄像机空间坐标系,为了对应于世界坐标系的XYZ,可以将其命名为UVN坐标系,它由之前提到的三个条件量构建而成:
选取视线的方向为N轴:N = eye–at;并归一化N。
选取up和N的叉积为U轴: U= up×N,并归一化U。
选取N和U叉积得到V轴:V = N×U,并归一化V。
https://blog.csdn.net/charlee44/category_8676774.html
https://blog.csdn.net/lufy_legend/category_9262828.html
齐次坐标(Homogeneous Coordinates) 其次坐标这个概念在第一次看real-time rendering 这本书的时候就有提起到,但当时看的一头雾水,只知道其次坐标在某些计算中比较方便,而事实上齐次坐标有着非常重要的意义和作用,主要是在处理三维透视方面,常用的几个地方,比如texture mapping 透视矫正,Projection Matrix的计算等等。
在笛卡尔坐标系中,两条平行线是永不相交的,而在现实中,两条平行线是可能相交于一点的,比如说下面的铁轨。
图一 . 铁路越来越窄,最后汇集到一点
在这种透视空间中,笛卡尔坐标就无法描述了。
解决方案就是齐次坐标,一句话解释,就是用N+1个数来表示N维空间中的点。
比如一个二维坐标(X,Y),它的齐次坐标就是(x, y, w), 关系如下
X = x/w Y = y/w 所以在知道齐次坐标的情况下,可以很方便地得到其笛卡尔坐标。之所以称之为其次坐标,是因为奇次坐标具有缩放不变性,比如(1,2,3),(2,4,6), (1a,2a,3a) 所表达的笛卡尔坐标是一样的!
有了其次坐标我们就可以证明两条平行线相交了。
有两条直线
Ax + By + C = 0
Ax + By + D = 0
很明显他们在平面内是平行线,永不相交(如果C==D的话,两条直线就重合了)
化为其次坐标,
A(x/w) + B(y/w) + C = 0;
A(x/w) + B(y/w) + D = 0;
同乘w,得到
Ax + By + Cw = 0
Ax + By + Dw = 0
则有解 (x,y,0),所以两条平行线相交在(x,y,0),也就是相交在无穷远的点。
位移矩阵
缩放矩阵
旋转矩阵是指绕着一个轴旋转一定的角度,绕x,y,z旋转的旋转矩阵可以记为:
