2020 CCPC Wannafly Winter Camp Day1 I K小数查询（线段树套权值线段树）

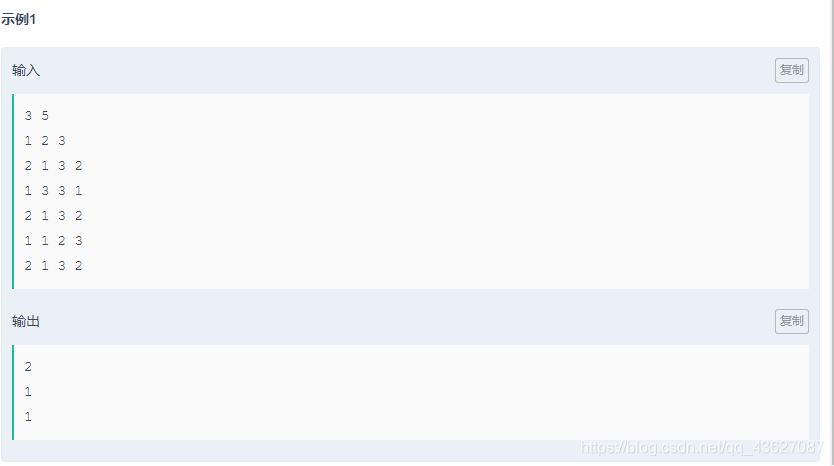
题意：

给定一个长度为 $n$ 的序列 $A$ 和 $m$ 次操作。
操作分两种：

• $(1,l,r,x) \left(1\leq l\leq r\leq n,\ 1\leq x\leq10^9\right)$ ，表示对 $\forall i\in\left[l,r\right]令 A_i=\min\left(A_i,x\right)$
• $(2,l,r,k) \left(1\leq l\leq r\leq n,\ 1\leq k\leq r-l+1\right)$ ，表示询问序列的第 $l\sim rl∼r$ 项中第 $k$ 小的数。

此时转化为一个经典的区间最值操作线段树问题。
维护区间最大值 $mx$ 、次大值 $sx$ 和最大值的出现次数 $ct$ 即可。
修改时：

• 若 $mx\leq x$ ，直接返回即可。

• 若 $sx\leq x<mx$$ ，直接修改并打上一个 $Lazy Tag$ .

• 若 $x<sx$ ，递归向下修改再 $push_up$ 上传信息。
  第三种情况下的修改非常暴力，时间复杂度主要取决于它。

在区间线段树的每个结点开一棵权值线段树记录区间每种权值的出现次数。

考虑到空间问题，要以动态开点的形式开权值线段树，空间复杂度： $O\left(n\log n\right)$.

维护该树套树之后，单次询问可在 $O\left(\log n\right)$ 棵权值线段树上二分，在 $O\left(\log^2n\right)$ 的时间内求解。

同样的，时间复杂度的瓶颈在修改操作上。
采用势能分析法分析：
修改在弱化版的基础上多了一个权值线段树合并的操作。
最初，所有内层权值线段树叶子结点的总数为 $O\left(n\log n\right)$ 级别。
修改等价于将内层权值线段树中所有大于 $x$ 的结点并到 $x$ 的位置。
若修改定位到区间线段树的某一结点后，该结点的内层权值线段树合并了 $t$ 个结点。
由于会影响祖先结点，这次修改的时间复杂度是 $O\left(t\log^2n\right)$
这次修改之后，所有内层权值线段树叶子结点的减少量至少为 $t$ .
由于所有的 $t$ 之和不超过 $O\left(n\log n\right)$ ，所以最终合并的结点数是 $O\left(n\log n\right)$级别。

AC代码：

#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>
#include <cmath>
#include <map>
#include <set>
#include <string>
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <stack>
#include <queue>
using namespace std;
#define sd(n) scanf("%d", &n)
#define sdd(n, m) scanf("%d%d", &n, &m)
#define sddd(n, m, k) scanf("%d%d%d", &n, &m, &k)
#define pd(n) printf("%d\n", n)
#define pc(n) printf("%c", n)
#define pdd(n, m) printf("%d %d\n", n, m)
#define pld(n) printf("%lld\n", n)
#define pldd(n, m) printf("%lld %lld\n", n, m)
#define sld(n) scanf("%lld", &n)
#define sldd(n, m) scanf("%lld%lld", &n, &m)
#define slddd(n, m, k) scanf("%lld%lld%lld", &n, &m, &k)
#define sf(n) scanf("%lf", &n)
#define sc(n) scanf("%c", &n)
#define sff(n, m) scanf("%lf%lf", &n, &m)
#define sfff(n, m, k) scanf("%lf%lf%lf", &n, &m, &k)
#define ss(str) scanf("%s", str)
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define per(i, a, n) for (int i = n; i >= a; i--)
#define mem(a, n) memset(a, n, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define pb push_back
#define all(x) (x).begin(), (x).end()
#define fi first
#define se second
#define mod(x) ((x) % MOD)
#define gcd(a, b) __gcd(a, b)
#define lowbit(x) (x & -x)
typedef pair<int, int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int MOD = 1e9 + 7;
const double eps = 1e-9;
const ll INF = 0x3f3f3f3f3f3f3f3fll;
const int inf = 0x3f3f3f3f;
inline int read()
{
    int ret = 0, sgn = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            sgn = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        ret = ret * 10 + ch - '0';
        ch = getchar();
    }
    return ret * sgn;
}
inline void Out(int a) //Êä³öÍâ¹Ò
{
    if (a > 9)
        Out(a / 10);
    putchar(a % 10 + '0');
}

ll gcd(ll a, ll b)
{
    return b == 0 ? a : gcd(b, a % b);
}

ll lcm(ll a, ll b)
{
    return a * b / gcd(a, b);
}
///快速幂m^k%mod
ll qpow(ll a, ll b, ll mod)
{
    if (a >= mod)
        a = a % mod + mod;
    ll ans = 1;
    while (b)
    {
        if (b & 1)
        {
            ans = ans * a;
            if (ans >= mod)
                ans = ans % mod + mod;
        }
        a *= a;
        if (a >= mod)
            a = a % mod + mod;
        b >>= 1;
    }
    return ans;
}

// 快速幂求逆元
int Fermat(int a, int p) //费马求a关于b的逆元
{
    return qpow(a, p - 2, p);
}

///扩展欧几里得
ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    ll g = exgcd(b, a % b, x, y);
    ll t = x;
    x = y;
    y = t - a / b * y;
    return g;
}

#define ls (rt << 1)
#define rs (rt << 1 | 1)
#define mid ((l + r) >> 1)

const int N = 8e4 + 5;
const int M = 3e7 + 5;
int n, m, a[N];
int tr[N << 2], mx[N << 2], sx[N << 2], ct[N << 2], tg[N << 2];
int tp, id, de[M], sz[M], lf[M], rg[M];
vector<int> ur;

void solve(void);
void build(int rt, int l, int r);
void recycle(int rt);
int modify(int rt, int l, int r, int x, int y, int v);
void get_rt(int rt, int l, int r, int x, int y);
int get_kth(int l, int r, int k);
void push_up(int rt);
void push_down(int rt);
void mdf(int rt, int v);
void ins(int &rt, int l, int r, int x, int d);
int merge0(int a, int b);
int merge1(int a, int b);
void merge2(int &a, int b);
int node();
void del(int rt);

int node() { return tp ? de[tp--] : ++id; }

void del(int rt) { de[++tp] = rt, sz[rt] = lf[rt] = rg[rt] = 0; }

void ins(int &rt, int l, int r, int x, int d)
{
    if (!rt)
        rt = node();
    sz[rt] += d;
    if (l == r)
        return;
    x > mid ? ins(rg[rt], mid + 1, r, x, d) : ins(lf[rt], l, mid, x, d);
}

void push_up(int rt)
{
    if (mx[ls] < mx[rs])
        mx[rt] = mx[rs], sx[rt] = max(mx[ls], sx[rs]), ct[rt] = ct[rs];
    else if (mx[ls] > mx[rs])
        mx[rt] = mx[ls], sx[rt] = max(sx[ls], mx[rs]), ct[rt] = ct[ls];
    if (mx[ls] ^ mx[rs])
        return;
    mx[rt] = mx[ls], sx[rt] = max(sx[ls], sx[rs]), ct[rt] = ct[ls] + ct[rs];
}

void push_down(int rt)
{
    if (tg[rt])
        mdf(ls, tg[rt]), mdf(rs, tg[rt]), tg[rt] = 0;
}

int merge0(int a, int b)
{
    if (!a && !b)
        return 0;
    int r = node();
    sz[r] = sz[a] + sz[b];
    lf[r] = merge0(lf[a], lf[b]), rg[r] = merge0(rg[a], rg[b]);
    return r;
}

int merge1(int a, int b)
{
    if (!a || !b)
        return a | b;
    sz[a] += sz[b], lf[a] = merge1(lf[a], lf[b]), rg[a] = merge1(rg[a], rg[b]);
    return del(b), a;
}

void merge2(int &a, int b)
{
    if (!b)
        return;
    if (!a)
        a = node();
    sz[a] += sz[b], merge2(lf[a], lf[b]), merge2(rg[a], rg[b]);
    if (!sz[a])
        del(a), a = 0;
}


void build(int rt, int l, int r)
{
    if (l == r)
        return ins(tr[rt], 1, n, mx[rt] = a[l], ct[rt] = 1);
    build(ls, l, mid), build(rs, mid + 1, r);
    tr[rt] = merge0(tr[ls], tr[rs]), push_up(rt);
}

void recycle(int rt)
{
    if (!rt)
        return;
    recycle(lf[rt]), recycle(rg[rt]), del(rt);
}

int modify(int rt, int l, int r, int x, int y, int v)
{
    if (r < x || y < l || mx[rt] <= v)
        return 0;
    if (x <= l && r <= y && sx[rt] < v)
    {
        int c = 0;
        ins(c, 1, n, mx[rt], -ct[rt]), ins(c, 1, n, v, ct[rt]), mdf(rt, v);
        return c;
    }
    push_down(rt);
    int c = modify(ls, l, mid, x, y, v);
    c = merge1(c, modify(rs, mid + 1, r, x, y, v));
    merge2(tr[rt], c), push_up(rt);
    return c;
}

void get_rt(int rt, int l, int r, int x, int y)
{
    if (r < x || y < l)
        return;
    if (x <= l && r <= y)
        return ur.push_back(tr[rt]);
    push_down(rt), get_rt(ls, l, mid, x, y), get_rt(rs, mid + 1, r, x, y);
}

int get_kth(int l, int r, int k)
{
    if (l == r)
        return l;
    int lsz = 0;
    for (int i : ur)
        lsz += sz[lf[i]];
    if (lsz >= k)
    {
        for (int &i : ur)
            i = lf[i];
        return get_kth(l, mid, k);
    }
    for (int &i : ur)
        i = rg[i];
    return get_kth(mid + 1, r, k - lsz);
}

void mdf(int rt, int v)
{
    if (v >= mx[rt])
        return;
    ins(tr[rt], 1, n, mx[rt], -ct[rt]), ins(tr[rt], 1, n, v, ct[rt]);
    mx[rt] = tg[rt] = v;
}

int main()
{
    sdd(n, m);
    for (int i = 1; i <= n; i++)
        sd(a[i]);
    build(1, 1, n);
    for (int i = 1, op, l, r, x; i <= m; i++)
    {
        scanf("%d%d%d%d", &op, &l, &r, &x);
        if (op == 1)
            recycle(modify(1, 1, n, l, r, x));
        else
        {
            ur.clear();
            get_rt(1, 1, n, l, r);
            printf("%d\n", get_kth(1, n, x));
        }
    }
    return 0;
}