Leetcode 375 (DP O(n^2)解法)

题意

对方从1～n里面选一个数字，然后我来猜，每次猜后，对方会告诉我是大了，小了，还是正确。假如我猜 $x$，猜错的的话要付给他 $x$元前，问我得钱包里至少放多少钱才能保证我能猜到他的数字。

O(n^3) 解法

这个题 $O(n^3)$解法是容易想到的，状态转移方程如下：
$f(a,b)=\min_{a\le k\le b}\Big(\max\big\{ f(a,k-1),f(k+1,b)\big\}+k\Big)\ .$
这里 $f(a, b)$代表正确数字在区间 $[a, b]$内时，钱包里至少放的钱。而 $k$代表我本次想猜的的数字。用三层循环，第一层枚举左端点 $l$，第二层枚举左端点 $r$，第三层枚举中间选取的数字 $k$，最后答案就是 $f(1, n)$。

O(n^2) 解法

这时候我们用两层循环来解这个题，前两层循环与 $n^3$解法一样。这里最重要的是如何用 $O(1)$的时间求 $f(a, b)$的值。

这里观察到随着 $k$的增长， $f(a,k-1)$是一个单调递增的函数，而 $f(k+1,b)$是一个单调递减的函数，然后我们可以利用这个性质来分别求解 $f(a,k-1) + k$ 和 $f(k+1,b) + k$，然后取二者的小的那个值即可。

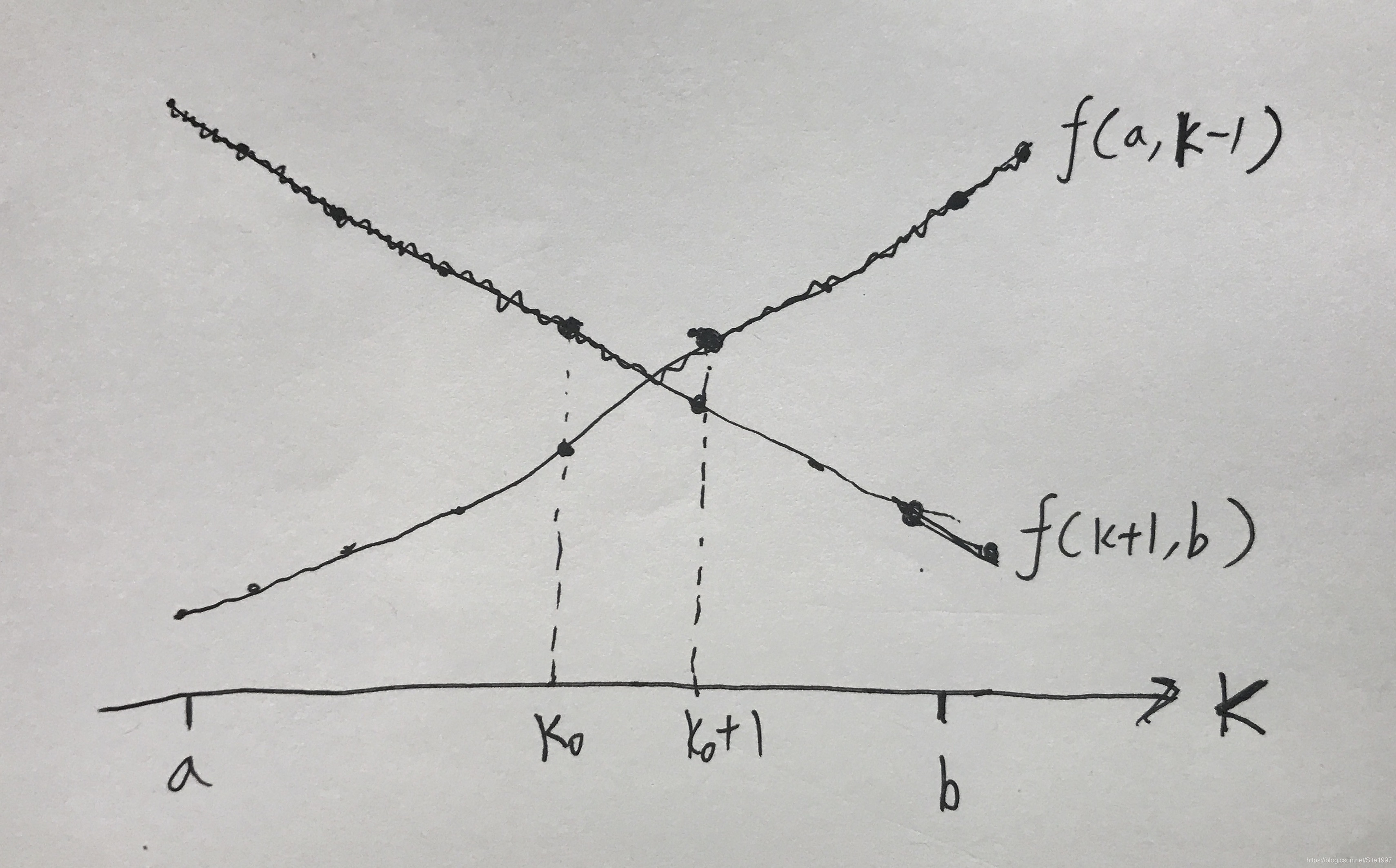
这里我们先用 $O(1)$的时间找出两个函数的“交点”，记为 $k_0$，如下图所示。

1. 对于 $f(a,k-1) + k$而言，它是个单调递增的函数。于是，在第二层循环里我们每次保存上一次所找到的 $k_0$值，并随着 $l$减小向左移动一点（因为第二层循环随着左端点 $a$减小，两条曲线交点在缓慢左移），直到刚好 $f(a,k-1) \leq f(k+1,b)$为止。这时 $f(a, k_0) + k_0 + 1$就是它的最小值。
2. 对于 $f(k+1,b) + k$而言，我们并不能判断它的增长趋势，因为 $f(k+1, b)$是单减，而 $k$是单增，我们无法利用函数本身的单调性处理。这时候我们用采用deque来保存一个单调性，每次拿到最小元素，并且将当前 $f(l, r)$插入deque中手动维护单调性即可。这里deque最末尾的元素也就是这一项的最小值。

最后，我们再取这两项之间的最小值，赋值给 $f(a, b)$。

代码

const int INF = 0x3f3f3f3f;
class Solution {
public:
    
    vector<vector<int>> dp;
    
    int getMoneyAmount(int n) {
        dp = vector<vector<int>>(n+5, vector<int>(n+5, 0));
        for (int r=2; r<=n; r++) {
            int k = r-1;
            //        <k  , dp[l+1][r] + l>
            deque< pair<int, int> > dq;
            for (int l=r-1; l>0; l--) {
                while (k > 0 && dp[l][k-1] > dp[k+1][r])
                    k --;
                // get rid of idx that is lager than k
                while (!dq.empty() && dq.back().first > k)
                    dq.pop_back();
                // insert current dp[l+1][r] + l into deque
                int dpVal = dp[l+1][r] + l;
                while (!dq.empty() && dq.front().second > dpVal)
                    dq.pop_front();
                dq.push_front(make_pair(l, dpVal));
                dp[l][r] = min(dp[l][k] + k + 1, dq.back().second);
            }
        }
        return dp[1][n];
    }
};

参考文献

OTZ
https://artofproblemsolving.com/community/c296841h1273742