引言
前面我们说了Routh判据,貌似很好用了,毕竟只需要得到代数式的系数就可以判断一个系统的稳定性,那为什么这里需要再提Nyquist判据呢?
很简单,因为我们不想要用代数式…
Nyquist判据就是一个频域稳定判据,利用我们前面说的Nyquist曲线
另外还有一个对数稳定性判据,显然是对Bode图的方法
下面我们就看看Nyquist判据到底是什么回事吧
Nyquist判据的形式
前面我们学到,如果一个系统的闭环极点都在虚轴左边的话,那这个系统就是稳定的
现在我们用 Z 表示在虚轴右边的闭环极点个数,显然 Z = 0 时,系统稳定
Nyquist判据公式:
Z = P - 2N
p - 在虚轴右边的开环极点个数
N - 从( -1, j0 )看,Nyquist曲线包围该点的圈数
{顺时针为负,逆时针为正}
Nyquist判据的理解
我觉得作为学生,不能说只做到知其然,我看到很多学生,针对这个知识点,记住了公式就感觉万事大吉,其实理解一下并不需要太多时间,在你遇到各种题目的时候,也能更好得使用他去解决问题,而不是就知道哭喊难。
Nyquist判据是依靠数学复变中的幅角原理证明的,我们面向应用并不需要去了解完整的推到过程,我们只需要知道大概的公式由来,由此加强理解就好
现在有一个最基本的单反馈系统
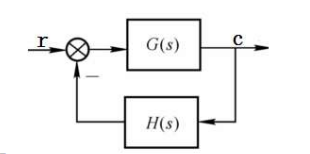
显然:
开环函数:GH(S) = k'M(s)/N(s)
闭环函数:G/[1+GH(S)]
由于我们关心的是 极点,所以我们构造
辅助函数:F(S) = 1 + GH(S) = K'M(S)+N(S) /N(S) =D(S)/N(S) = 闭环极点/开环极点
同时,我们知道辅助函数的频率特性就是开环传递函数右移一个单位
这里引进一个Nyquist路径,就是从原点沿轴向上一直到无穷,在从虚轴右边以无穷为半径画圆,一直到虚轴负半轴无穷处,再返回原点,形状是一个半圆
当s按照该路径绕一周,我们计算该传递函数的转动角(零点 - 极点)
我们发现按照上面说的,顺时针负,逆时针正的计算方法,我们发现,
所有虚轴右半边的点被包含在内,转圈为 顺时针360,为 -2π
所有在半圆外的点,都为0
所以最后得到的角度为 -2π(Z - P) = 2π(P - Z) = 2π R
所以我们只有知道R就可以由P算出Z,从而判断出系统的稳定性
现在我们把这个图映射到Nyquist曲线图中
显然
1.从原点一直向上到无穷的部分对应我们的Nyquist曲线
2.从虚轴无穷小到原点的部分可以看做 Nyquist曲线的对称线
3.圆弧对应的是原点,不过对应的方向不同,但针对一个点没有方向可言
所以我们得到了系统函数的开环传递函数的Nyquist曲线,就可通过对称画出完整的奈氏路径图对应的Nyquist曲线
向右平移一个单位得到了我们要的辅助函数F(S)图,我们计算原点对其的旋转圈数得到R
按理说我们完成了预期中的所有步骤,但为了简化计算过程,我们做题时候不需要画完整路径对应图并平移
简化:
1.平移后对应计算的是原点,那我们直接计算从( -1,j0 )看曲线的旋转圈数即可
2.上面说了路径图是对称的两个Nyquist图,所以我们只需要计算( -1,j0 )看Nyquist曲线的圈数×2即可
到此我们可以完全理解上面的解题公式是为何如此了
