对于上一部分中的问题算法介绍。运行时间花费了120s,当然配置稍微低点的会花费更久的时间。并且如果将1000改为10000,甚至更高,那么花费的时间将会更加高。这里有没有一种方法对该算法进行优化呢?
对于该问题,我们不难发现,对于已经确定的a,b,那么c是唯一确定的,因为
,有了这样的一个思想,我们对上述代码进行改进
import time
start_time = time.time()
for a in range(1001):
for b in range(1001):
c = 1000-a-b
if a**2+b**2==c**2:
print("a,b,c:%d,%d,%d"%(a,b,c))
end_time = time.time()
print("time:%d"%(end_time-start_time))
print('finished')
结果
a,b,c:0,500,500
a,b,c:200,375,425
a,b,c:375,200,425
a,b,c:500,0,500
time:0
finished
与之前进行对比发现,改进后的代码运行时间少了很多,花费不到1秒时间
那么我们应该如何来衡量算法的效率呢?下面有几种方式
算法效率衡量
执行时间反应算法效率
对于同一个问题,我们给出了两种算法,通过对时间的测算,发现两种算法的运行时间相差巨大(214秒相对于0.18秒),由此我们得出的结论:实现算法程序的时间可以反应出算法的效率,即算法的优略。
单靠时间值绝对可信吗?
假设我们将第二次尝试的算法在一台古老的计算机上运行,情况会如何?可能运行的时间并不会比第一种算法少多少。
单纯依靠运行时间来比较算法的优略不一定是客观准确的!
程序的运行离不开计算机环境(包括硬件和操作系统),这些客观远影会影响程序运行的速度并反应在程序的执行时间上,那么如何才能客观的评价一个算法的优略呢?
时间复杂度和“大O表示法”
我们假定计算机执行算法每一个基本操作的时间是固定的一个时间单位,那么有多少个基本操作就代表会花费多少时间单位。对于不同的计算环境而言,确切的时间是不同的,但是对于算法进行多少个基本操作(即花费多少时间单位)在规模量级上却是相同的,由此可以忽略机器环境的影响而客观的反应算法的时间效率。
对于算法的时间效率,我们用“大O记法”来表示。
“大O记法”:对于单调的整数函数f,如果存在一个整数函数
和实常数
,使得对于充分大的n总有
,就说函数g是f的一个渐进函数(忽略常数),计作
,也就是说,在趋向于无穷的极限意义下,函数f的增长速度受到函数g的约束,亦即函数f与函数g的特征相似。
时间复杂度:假设存在函数g,使得算法A处理规模为n的问题示例所用时间为
,则称
为算法A的渐进时间复杂度,简称时间复杂度,记为
如何理解“大O记法”
对于算法进行特别具体的细致分析虽然很好,但在实践中的实际价值有限。对于算法的时间性质和空间性质,最重要的是其数量级和趋势,这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计,例如,可以认为
和
属于同一个量级,如果两个算法处理同样规模实例的代价分别为这两个函数,就认为他们的效率“差不多”,都为
级。
比较两种算法
for a in range(1001):
for b in range(1001):
for c in range(1001):
if a+b+c==1000 and a**2+b**2==c**2:
print("a,b,c:%d,%d,%d"%(a,b,c))
和
for a in range(1001):
for b in range(1001):
c = 1000-a-b
if a**2+b**2==c**2:
print("a,b,c:%d,%d,%d"%(a,b,c))
第一种算法包括三种循环,而if语句中的2个基本步骤(未细分,细分是10),其时间复杂度为
T = 1000 * 1000 * 1000 * 2
当我们把原问题中的1000改为2000,那么时间复杂度变为
T = 2000 * 2000 * 2000 * 2
抽象化问题,即当a+b+c=N时,N仅为问题的规模,那么时间复杂度变为
T = N * N * N * 2
则最终的时间复杂度是和你解决问题的规模有关系,即时间复杂度
T(n) = * 2
大O记法认为我们的时间复杂度 * 2(未细分)和 * 10(细分)具有同一个量级 ,不管其后面是乘以2还是10,其时间复杂度都是在一个级别上的,故其时间复杂度均为
T(n) =
用大O记法的表示就是
同理,对于第2种算法,其时间复杂度用大O记法表示就是
最坏时间复杂度
分析算法时,存在几种可能的考虑:
- 算法完成工作最少需要多少基本步骤,即最优时间复杂度
- 算法完成工作最多需要多少基本步骤,即最坏时间复杂度
- 算法完成工作平均需要多少基本步骤,即平均时间复杂度
对于最优时间复杂度,其价值不大,因为它没有提供什么有用信息,其反应的只是最乐观最理想的情况,没有参考价值。
对于最坏时间复杂度,其提供了一种保证,表明算法在此程度的基本操作中一定可以完成工作。
对于平均时间复杂度,是对算法的一个全面评价,因此它完整全面的反应了这个算法的性质,但另一方面,这种衡量并没有保证,不是每个计算都能在这个基本操作内完成,而且,对于平均情况的计算,也会因为应用算法的实例分布可能并不均匀而难以计算。
因此,我们主要关注算法的最坏情况,亦即最坏时间复杂度
时间复杂度的几条基本计算规则
- 基本操作,它只有常数项,认为其时间复杂度为O(1),比如算法中的if语句,其并不与n有关系。
- 顺序结构,时间复杂度按加法进行计算。指对基本操作的累加。
- 循环结构,时间复杂度按乘法进行计算
- 分支结构,时间复杂度取最大值
- 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其他次要项和常数项可以忽略。
- 在没有特殊说明时,我们所分析的时间复杂度都是指最坏时间复杂度
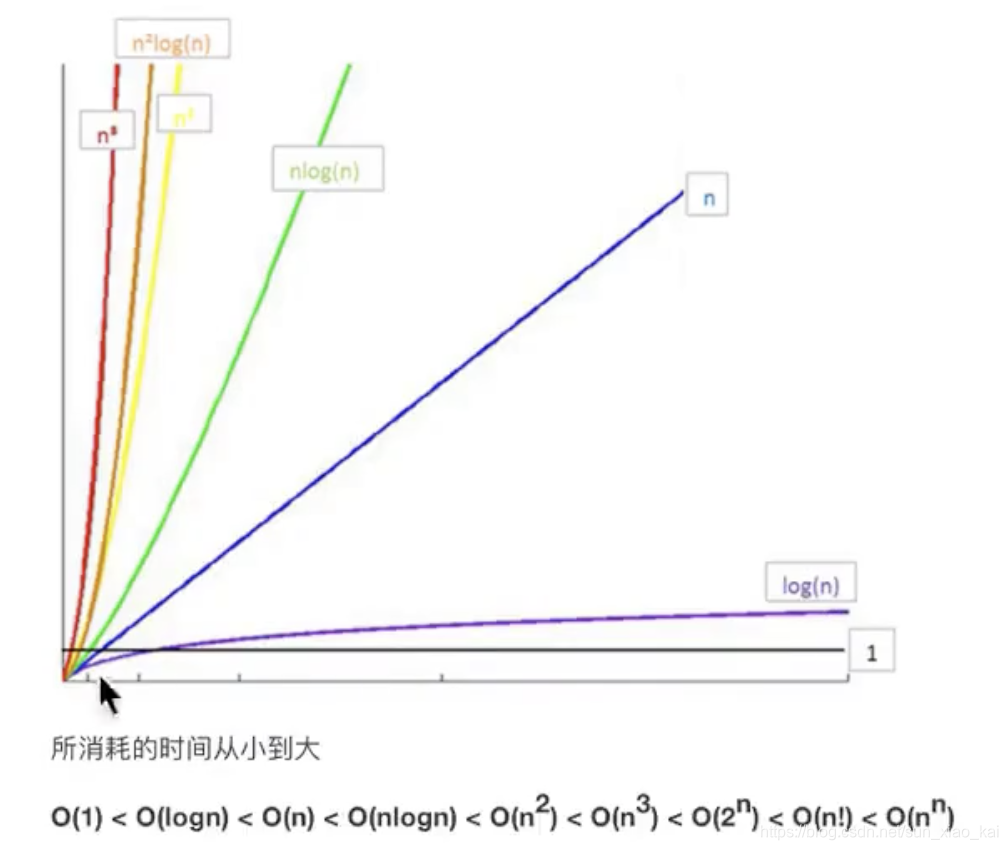
常见时间复杂度
| 执行次数函数 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 平方阶 | ||
| 对数阶 | ||
| nlogn阶 | ||
| 立方阶 | ||
| 指数阶 |
注意,经常将