Description
给定n个点,m条边的无向图(无自环),可以从图中删除一条边,问删除哪些边可以使图变成一个二分图。
Input
第1行包含两个整数n,m,分别表示点数和边数。
第2~m+1行每行两个数x,y,表示有一条边连接点x,y。
Output
第一行两个整数,表示能删除的边的个数。
接下来一行按照从小到大的顺序输出能删除的边的编号。
Sample Input
4 4
1 2
1 3
2 4
3 4
Sample Output
4
1 2 3 4
Hint
10%的数据,n,m<=10
40%的数据,n,m<=1000
70%的数据,n,m<=100000
100%的数据,n,m<=2000000
思路
首先一个图是二分图的充要条件是这个图不存在奇环
所以就可以分成三种情况来讨论一下:
①:图中没有奇环,此时随便乱删都满足条件。
②:图中有奇环,此时删除的边必须满足它是所有奇环的公共边。
那么现在我们对这个图建出一棵 DFS 树。
容易得出,图中除了树边就是从一个点连向他的祖先的边,我们将它记为返祖边 (图中红色边)。
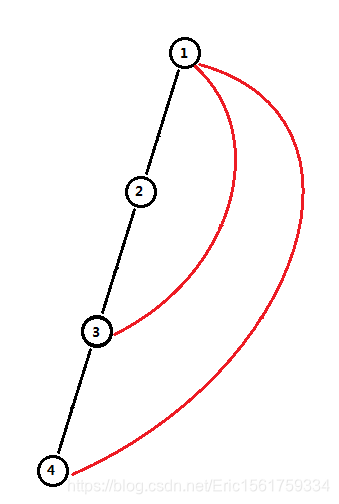
比较显然的是,返祖边 (a,b) 和 树上路径 (b,a) 可以在图中形成一个环。
如图 3→1→2→3 形成了一个奇环,4→1→2→3→4 形成了一个偶环。
那么这个问题的思路就比较清晰了,首先求出只包含一条返祖边的奇环的个数。
不妨将只包含一条返祖边的环记为单祖环,很显然有:
①:如果图中没有单祖奇环,那么删除图中任何一条边都满足条件。
②:如果图中有单祖奇环,那么删除的边必须满足是所有单祖奇环的公共边。
现在只讨论图中有单祖奇环的情况
删除返祖边能否满足条件
①:如果只有一个单祖奇环, 那么删除单祖奇环中的返祖边一定满足条件。
②:如果有超过一个单祖奇环, 那么删除任何一条返祖边都不满足条件。(返祖边不是所有单祖奇环的公共边)
删除树边能否满足条件
此时只考虑树边是否能被所有单祖奇环经过,那么如果 (a,b) 是返祖边,树上的链 (b,a) 都在环上。
如果树边在 所有的单祖奇环上又不在任何一个单祖偶环上,那么删去这条边是满足条件的。
为什么还要看偶环呢?
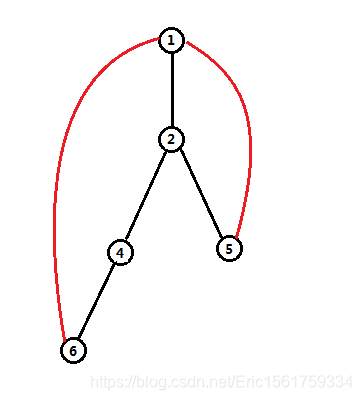
一个很显然的奇环是 5→1→2→5, 这个奇环只包含一条返祖边 (5,1)。
但是这个图只有删去 (2,5) 或 (1,5)可以使得图中没有奇环。
(如果删去 (1,2) ,图中还是存在奇环 6→1→5→2→4→6,这个奇环包含两条返祖边)
你可能已经发现了,在之前我们只考虑了只包含一条返祖边的奇环,而事实上奇环也可能包含两条返祖边。
如果边 (a,b) 在单祖奇环 X 中又在单祖偶环 Y中, 那么即使删除这条边,X 和 Y 仍然能形成一个奇环。
所以判断删除树边能否满足条件是需要判断单祖偶环的。
这样我们就dp求一下奇环和偶环就好了
设 F[i] 为点 i 的父边被多少个单祖奇环包含,G[i] 为点 i 的父边被多少个单祖偶环包含。
在 DFS树 中自底向上 DP。
考虑点 u,对于边 (u, v),有三种情况:
①:(u, v) 是树边,点 u 是 v 的父亲,F[u] += F[v], G[u] += G[v]
②:(u, v) 是一条返祖边, F[u]++ 或 G[u]++;
③:(v, u) 是一条返祖边, F[u]- - 或 G[u]- -;
时间复杂度:O(n+m)
代码
#include<bits/stdc++.h>
using namespace std;
const int M=4e6+77;
typedef int arr[M];
arr to,g,nx,val,dfn,dep,fa;
int f[2][M],ans[M],tot[2][M];
int df,cnt,sum,n,m,x[M],y[M];
void add(int u,int v,int w)
{
to[++cnt]=g[u]; nx[cnt]=v; g[u]=cnt; val[cnt]=w;
}
void dfs(int u,int ff)
{
dfn[u]=++df;
for(int i=g[u];i;i=to[i])
{
int v=nx[i];int w=val[i];
if(w==fa[u])continue;
if(dfn[v])
{
if(dep[v]==dep[u])
{
if(dfn[u]<dfn[v]) f[1][u]--;
else
{
++sum; f[1][u]++; tot[1][w]++;
}
}
else
{
if(dfn[u]<dfn[v]) f[0][u]--;else
{
f[0][u]++;
tot[0][w]++;
}
}
continue;
}
fa[v]=w;
dep[v]=dep[u]^1;
dfs(v,u);
for(int j=0;j<2;++j)
{
tot[j][w]+=f[j][v];
f[j][u]+=f[j][v];
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<m;++i)
{
scanf("%d%d",&x[i],&y[i]);
add(x[i],y[i],i);
add(y[i],x[i],i);
}
for(int i=1;i<=n;++i)
{
if(!dfn[i])
{
dep[i]=1;
dfs(i,i);
}
}
if(!sum)
{
printf("%d\n",m);
for(int i=1;i<=m;++i)printf("%d ",i);
return 0;
}
memset(ans,0,sizeof ans);
for(int i=0;i<m;++i)
{
if(!tot[0][i]&&tot[1][i]==sum)ans[++ans[0]]=i;
}
printf("%d\n",ans[0]);
for(int i=1;i<=ans[0];++i)printf("%d ",ans[i]+1);
return 0;
}
