一、搜索树的复杂度分析
- 本文考察二叉搜索树和索引二叉搜索树
- 二叉搜索树的渐进性能可以和跳表媲美:
- 查找、插入、删除操作所需的平均时间为Θ(logn)
- 查找、插入、删除操作的最坏情况的时间为Θ(n)
- 元素按升序输出时所需时间为Θ(n)
- 虽然在最坏情况下的查找、插入、删除操作,散列表和二叉搜索树的时间性能相同,但是散列表在最好的情况下具有超级性能Θ(1)
- 不过,对于一个指定的关键字,使用二叉搜索树,你可以在Θ(n)时间内,找到最接近它的关键字。例如,给定关键字是k,你可以在Θ(n)时间内,找到最接近k的关键字(即小于等于k的最大关键字,或大于等于k的最小关键字)。而对于散列表来说,这种操作的时间是Θ(n+D)(其中D是散列表除数);对跳表来说,这种操作的时间是Θ(logn)
- 索引二叉搜索树:
- 使用索引二叉搜索树,你可以按关键字和按名次进行字典操作,例如读取关键字从小打到排名第10的元素,删除关键字从小打到第100的元素。按名次的操作和按关键字的操作,其时间性能一样
- 索引二叉树可以用来表示线性表;其中的元素具有名次(即索引),没有关键字。在这种线性表的表示中,get、erase、insert操作的时间性能为O(logn),但是前面实现的线性表,这些操作的时间为Θ(n)(不过get操作在用数组实现时,其性能是Θ(1))
- 总结,对于二叉搜索树和跳表来说,在最坏和最好情况下的渐近时间复杂性是相同的。但是,我们可以对二叉搜索树加以平衡限制,使上述的每一个操作耗时都是Θ(logn)
二、搜索树的高效性
三、二叉搜索树
- 概述:二叉搜索树是一棵二叉树,可能为空
- 一棵非空的二叉搜索树满足以下特征:
- 1.每个元素都有一个关键字,并且任意两个元素的关键字都不同;因此,所有的关键字都是唯一的(其实也可以不唯一,见下)
- 2.在根节点的左子树中,元素的关键字(如果有的话)都小于根节点的关键字
- 3.在根节点的右子树中,元素的关键字(如果有的话)都大于根节点的关键字
- 4.根节点的左、右子树也都是二叉搜索树
- 例如下面图a)不是二叉搜索树,图b)和c)都是二叉搜索树

- 如果关键字不唯一,那么这样的二叉树称为“有重复值的二叉搜索树”
二叉搜索树的查找
- 二叉搜索树的查找步骤如下:
- 1.从根开始,如果根节点为空,就停止搜索;如果不为空,进行第2步
- 2.将要查找的元素与根节点进行比较,如果比根节点值小,就向左孩子查找;如果比根节点值大,就向右孩子查找
- 3.重复2步骤,只要比某个节点值小就向左孩子查找;只要比某个节点值大,就向右孩子查找
- 4.查找到之后返回查找的节点,如果没查找就返回空
二叉搜索树的插入
- 二叉搜索树的插入步骤如下:
- 1.从根开始,如果根节点为空,就将新节点作为根节点;如果不为空进行第二步
- 2.将要插入的节点与根节点相比较,遇键值较大者就向左,遇键值较小者就向右
- 3.如果遇到节点的值与插入节点的值相同就退出停止插入(或做其他处理)
- 4.一直到尾端,即为插入点
- 例如:
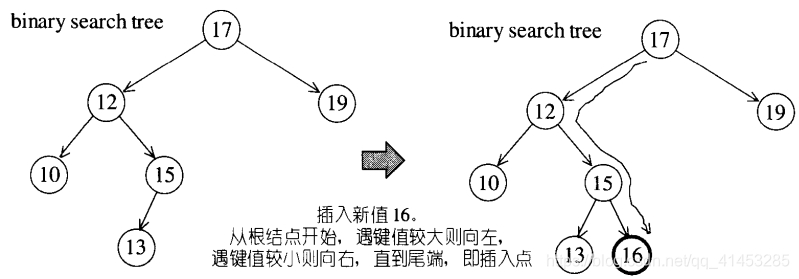
二叉搜索树的删除
- 删除节点p,要考虑3种情况:
- 1.p是树叶
- 2.p只有一棵非空子树
- 3.p有两颗非空子树
- ①如果删除的是树叶:
- 1.如果删除的节点是叶节点:就释放该叶节点。例如,下面删除图a中的节点35,直接将其父节点40的左孩子域置为NULL即可,结果如图b所示
- 2.如果删除的节点是根节点(说明树总共只有一个节点):直接令根为NULL

- ②如果删除的节点只有一棵非空子树:
- 1.如果删除的节点是根节点:就另其唯一的子节点作为新的根节点
- 2.如果删除的节点不是根节点:直接将其子节点连至其父节点即可。例如下图想要删除节点5,直接将其子节点2作为父节点30的子节点即可

- ②如果删除的节点有两棵非空子树:
- 那么就将删除的节点替换为它的左子树中的最大元素或者替换为它的右子树中的最小元素
- 查找左子树的最大元素:先指向于左子树,然后一直向左子树的右子树进行查找,直到右孩子指针为NULL为止
- 查找右子树的最小元素:先指向于右子树,然后一直向右子树的左子树进行查找,直到左孩子指针为NULL为止
- 例如下面我们想删除图a中关键字为40的节点,既可以用右子树中的最小元素60来代替(如下图b所示),也可以用其左子树中的最大元素35来代替(如下图c所示)

四、索引二叉搜索树
- 概述:源于普通的二叉搜索树,只是在每个节点中添加一个leftSize域。这个域的值是该节点左子树的元素个数
- 下图是两棵索引二叉搜索树。节点内部的数字是元素的关键字,节点外的数组是leftSize的值

leftSize域索引的作用:
- leftSize同时给出了一个元素的索引(该元素的左子树的元素排在该元素之前)
- 例如在上图中:
- 元素按顺序分别为:12、15、18、20、25、30。按照线性表的形式(e0、e1、...e4)
- 根的索引时3,它等于根元素的leftSize域的值
- 在根为25的子树中,元素按顺序排列为25/30,根元素25的索引时0,而leftSize的值也是0
索引二叉搜索树的查找

- 带有索引的搜索方法与搜索偶对(一个偶对被定义为关键字域key和值域value)的方法是类似的
- 假设我们要查找索引为2的元素:
- 跟的leftSize域的值是3,因此,我们要查找的元素在根的左子树中(进一步说,我们要查找的元素在左子树的索引为2)
- 因为左子树的根(即15)的leftSize域的值为1,所以我们要查找的元素在15的右子树中
- 然而,在15的右子树中,待查元素的索引不再是2,因为15的右子树元素都排在15的左子树元素和15之后
- 为了确定待查元素在15的右子树中的索引,我们要用2减去leftSize+1(其中leftSize是15的leftSize值(1)),结果为2-(1+1)
- 15的右子树的根是18,它的leftSize域的值是0,因此待查元素便是18
- 所需时间为O(h),其中h是索引搜索树的高
索引二叉搜索树的插入
- 把一个元素插入索引二叉搜索树中,使用的过程类似于下面我们实现的二叉搜索树的find()函数(见下面代码)
- 不过要在根至新插入节点的路径上修改leftSize域的值
- 所需时间为O(h),其中h是索引搜索树的高
索引二叉搜索树的删除
- 通过索引实施删除的过程是:
- 首先按索引进行搜索,确定要删除的元素的位置
- 然后按照上面介绍的二叉搜索树的删除操作进行删除
- 接下来,如果需要,在从根节点到删除节点的路径上更新leftSize域
- 所需时间为O(h),其中h是索引搜索树的高
五、搜索树的抽象数据类型(ADT)
二叉搜索树的抽象数据模型

索引二叉搜索树的抽象数据类型
- 支持所有二叉搜索树的方法,另外索引二叉搜索树还支持按名次进行查找和删除操作

六、搜索树的抽象类
二叉搜索树的抽象类
template<class K,class E>
class bsTree:public dictionary<K,E>
{
public:
//按关键字升序输出
virtual void ascend()=0;
};
索引二叉搜索树
- 索引二叉搜索树具有二叉搜索树的全部方法(所以继承于bsTree就好),并且另外还支持按名次进行查找和删除操作
template<class K,class E>
class indexedBSTree:public bsTree<K,E>
{
public:
//根据给定的索引,返回其数对的指针
virtual pair<const K,E>* get(int)const=0;
//根据给定的索引,删除其数对
virtual void delete(int)=0;
};
七、二叉搜索树的编码实现
头文件定义
#include <iostream>
#include <utility>
#include <queue>
using std::cin;
using std::cout;
using std::endl;
using std::pair;
using std::queue;
字典类定义
template<typename K,typename E>
class dictionary
{
public:
virtual ~dictionary() = default;
virtual bool empty()const = 0; //判断字典是否为空
virtual int size()const = 0; //返回字典中数对的数目
virtual std::pair<K, E> *find(const K& theKey)const = 0; //返回匹配数对的指针
virtual void erase(const K& theKeys) = 0; //删除匹配的数对
virtual void insert(const std::pair<K, E>& theElement) = 0;//向字典中插入一个新的数对
};
二叉搜索树抽象类定义
template<typename K,typename E>
class bsTree :public dictionary<K, E>
{
public:
virtual void ascend()= 0;//按关键字升序输出搜索二叉树
};
二叉搜索树实现(binarySearchTree)
按关键字升序输出二叉树(ascend)
- 按关键字升序输出搜索二叉树,又由于binarySearchTree继承于linkedBinaryTree,所以直接调用linkedBinaryTree中的后续打印函数inOrderOutput()即可
template<typename K,typename E>
class binarySearchTree :public bsTree<K, E>,
public linkedBinaryTree<std::pair<const K,E>>
{
public:
//按关键字升序输出搜索二叉树(直接调用linkedBinaryTree中的中序遍历打印函数即可)
virtual void ascend() override {
inOrderOutput();
}
};
linkedBinaryTree中的__output函数需要改动一下
- 因为现在节点的数据类型为pair了,所以打印时不能直接打印pair数据类型,而是pair.first
static void __output(binaryTreeNode<T>* theNode) { std::cout << theNode->element.second << " "; }
判断是否为空(empty())、返回大小(size())
- empty():判断树是否为空
- size():判断树的大小
template<typename K,typename E>
class binarySearchTree :public bsTree<K, E>,
public linkedBinaryTree<std::pair<K,E>>
{
public:
virtual bool empty()const override{ //判断树是否为空
return (this->treeSize == 0);
}
virtual int size()const override { //返回树的大小
return this->treeSize;
}
};
查找节点函数(find)
/*根据关键字查找指定的节点,方法在上面有过介绍
如果关键字大于某节点,就向右子树中找;如果关键字小于某节点,就向左子树中找
*/
template<typename K,typename E>
std::pair<const K, E> *binarySearchTree<K,E>::find(const K& theKey)const
{
binaryTreeNode<std::pair<const K, E>> *tempNode = this->root;
while (tempNode != NULL)
{
if (theKey > tempNode->element.first)
tempNode = tempNode->rightChild;
else if (theKey < tempNode->element.first)
tempNode = tempNode->leftChild;
else
return &tempNode->element;
}
return NULL;
}
插入节点函数(insert)
- 根据上面二叉搜索树的插入规则,先遍历到搜索树的最后一个节点,然后进行插入
template<typename K, typename E>
void binarySearchTree<K, E>::insert(const std::pair<K, E>& theElement)
{
binaryTreeNode<std::pair<const K, E>> *tempNode = this->root,
*insertNode = NULL;
//遍历循环一直到树的叶子节点处即为插入点(或者找到一个有相同关键字的节点,更换值之后退出)
while (tempNode != NULL)
{
insertNode = tempNode;
if (tempNode->element.first > theElement.first)
tempNode = tempNode->leftChild;
else if (tempNode->element.first < theElement.first)
tempNode = tempNode->rightChild;
else {
tempNode->element.second = theElement.second;
return;
}
}
//新建立一个节点
binaryTreeNode<std::pair<const K, E>> *newNode =
new binaryTreeNode<std::pair<const K, E>>(theElement);
//如果根节点不为空
if (this->root != NULL) {
if (insertNode->element.first > newNode->element.first)
insertNode->leftChild = newNode;
else
insertNode->rightChild = newNode;
}
else//如果根节点为空,作为根节点
this->root = newNode;
this->treeSize++;
}
节点的删除函数(erase)
- 通过上面的删除规则,我们定义了如下函数,在函数中,如果要删除的节点有两颗非空子树,我们统一用左子树中的最大元素来进行替换
- 因为元素的数据类型为paie<const K,E>,这种删除操作时复杂的,而且改变关键字也是可能的,所以该算法的复杂性为O(h)
template<typename K, typename E>
void binarySearchTree<K, E>::erase(const K& theKey)
{
binaryTreeNode<std::pair<const K, E>> *eraseNode = this->root,
*beforeEraseNode = NULL;
//如果没遍历到默认,或者已经找到要删除的节点了(终止循环)
while (eraseNode != NULL&&eraseNode->element.first != theKey)
{
beforeEraseNode = eraseNode;
if (eraseNode->element.first>theKey)
eraseNode = eraseNode->leftChild;
else
eraseNode = eraseNode->rightChild;
}
//如果while循环完之后没有找到该节点,直接退出
if (eraseNode == NULL)
return;
//如果要删除的节点,左右子树都不为空(就将左子树中最大的节点移到删除节点处)
if ((eraseNode->leftChild != NULL) && (eraseNode->rightChild != NULL))
{
binaryTreeNode<std::pair<const K, E>> *p = eraseNode->leftChild,
*pp = eraseNode;
//一直遍历到左子树中的最右边的节点(即为左子树中的最大节点)
while (p->rightChild != NULL)
{
pp = p;
p = p->rightChild;
}
//然后将p移动到eraseNode处,并删除eraseNode
/*先创建一个指新节点,其值为要删除的节点左子树中最大节点的值,
但是左右子树指针为要删除的节点的左右子树指针,待会就用这个节点去填补删除节点
*/
binaryTreeNode<std::pair<const K, E>> *q =
new binaryTreeNode<std::pair<const K, E>>(p->element, eraseNode->leftChild, eraseNode->rightChild);
//如果删除的是根节点,直接把最大节点q赋值给根节点即可
if (beforeEraseNode == NULL)
this->root = q;
//如果删除的节点是其父节点的左子树,就其替换的节点作为其原父节点的左子树
else if (eraseNode == beforeEraseNode->leftChild)
beforeEraseNode->leftChild = q;
//同上,如果删除的节点使其父节点的右子树
else
beforeEraseNode->rightChild = q;
if (pp == eraseNode)
beforeEraseNode = q;
else
beforeEraseNode = pp;
//删除这个要删除的节点,然后将p赋值给它
delete eraseNode;
eraseNode = p;
}
}
主函数
int main()
{
binarySearchTree<int, char> y;
y.insert(pair<int, char>(1, 'a'));
y.insert(pair<int, char>(6, 'c'));
y.insert(pair<int, char>(4, 'b'));
y.insert(pair<int, char>(8, 'd'));
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << endl << endl;
pair<const int, char> *s = y.find(4);
cout << "Search for 4 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(4);
cout << "4 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << endl << endl;
s = y.find(8);
cout << "Search for 8 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(8);
cout << "8 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << endl << endl;
s = y.find(6);
cout << "Search for 6 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(6);
cout << "6 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
cout << endl << endl;
s = y.find(1);
cout << "Search for 1 succeeds " << endl;
cout << s->first << ' ' << s->second << endl;
y.erase(1);
cout << "1 deleted " << endl;
cout << "Tree size is " << y.size() << endl;
cout << "Elements in ascending order are" << endl;
y.ascend();
return 0;
}

八、代码下载
九、带有相同关键字元素的二叉搜索树
- 如果二叉搜索树可以带有相同的关键字,只需要把上面程序中的insert函数的while循环中的语句的else if中的<改为<=即可
while (tempNode != NULL)
{
insertNode = tempNode;
if (tempNode->element.first > theElement.first)
tempNode = tempNode->leftChild;
else if (tempNode->element.first <= theElement.first)
tempNode = tempNode->rightChild;
else {
tempNode->element.second = theElement.second;
return;
}
}
十、索引二叉搜索树编码实现
- 如果用编码实现索引二叉搜索树(indexedBinartSearchTree),一个节点的数值域是三元的:leftSize、key、value










