本文简述了一种三角形线性插值的方法(本文仅讨论二维情况)
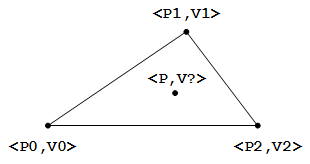
给定一个三角形的顶点坐标(P0, P1 和 P2 )以及对应的数值(V0, V1 和 V2 ),插值求解三角形内一点(坐标给定为P )的数值(V ).
问题说的有些抽象,给张图会清晰明了一些,图中的 V 即是我们想要插值求解的数值.
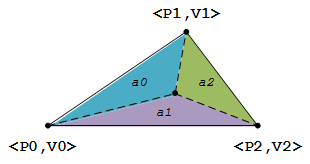
如何求解呢?一般我们是采用比例面积的方法,见下图(图中 a0, a1 和 a2 分别代表三个分割三角形的面积):
图中 a0 占三角形整体面积的比例代表 V2 (P2 对应的数值)占 V 的比例, a1 占三角形整体面积的比例代表 V1 (P1 对应的数值)占 V 的比例, 而 a2 占三角形整体面积的比例则代表 V0 (P0 对应的数值)占 V 的比例,假设三角形的整体面积为 a , 则我们有:
V
=
a
0
a
∗
V
2
+
a
1
a
∗
V
1
+
a
2
a
∗
V
0
=
(
a
0
∗
V
2
+
a
1
∗
V
1
+
a
2
∗
V
0
)
/
a
\begin{aligned} V & = \dfrac{a_0}{a} * V_2 + \dfrac{a_1}{a} * V_1 + \dfrac{a_2}{a} * V_0 \\ & = (a_0 * V_2 + a_1 * V_1 + a_2 * V_0) / a \end{aligned}
V = a a 0 ∗ V 2 + a a 1 ∗ V 1 + a a 2 ∗ V 0 = ( a 0 ∗ V 2 + a 1 ∗ V 1 + a 2 ∗ V 0 ) / a
接下来的问题就是如何根据三角形的顶点求解三角形的面积了,这里我们直接给出结论,有兴趣的朋友可以从这里 开始了解,方法就是使用叉积 :
假设三角形的三个顶点分别为 P0, P1 和 P2 , 则三角形面积 a 的计算公式为:
a
=
1
2
∗
∣
(
P
1
−
P
0
)
×
(
P
2
−
P
0
)
∣
a = \dfrac{1}{2} * | (P_1 - P_0) \times (P_2 - P_0) |
a = 2 1 ∗ ∣ ( P 1 − P 0 ) × ( P 2 − P 0 ) ∣
扫描二维码关注公众号,回复:
8814554 查看本文章
如果 P0 的坐标为 <x0, y0> , P1 的坐标为 <x1, y1> , P2 的坐标为 <x2, y2> ,则上面的公式可表达为:
a
=
1
2
∗
∣
(
P
1
−
P
0
)
×
(
P
2
−
P
0
)
∣
=
1
2
∗
∣
(
<
x
1
,
y
1
>
−
<
x
0
,
y
0
>
)
×
(
<
x
2
,
y
2
>
−
<
x
0
,
y
0
>
)
∣
=
1
2
∗
∣
(
<
x
1
−
x
0
,
y
1
−
y
0
>
)
×
(
<
x
2
−
x
0
,
y
2
−
y
0
>
)
∣
=
1
2
∗
∣
(
x
1
−
x
0
)
∗
(
y
2
−
y
0
)
−
(
x
2
−
x
0
)
∗
(
y
1
−
y
0
)
∣
\begin{aligned} a & = \dfrac{1}{2} * | (P_1 - P_0) \times (P_2 - P_0) | \\ & = \dfrac{1}{2} * |(<x_1, y_1> - <x_0, y_0>) \times (<x_2, y_2> - <x_0, y_0>) | \\ & = \dfrac{1}{2} * |(<x_1 - x_0, y_1 - y_0>) \times (<x_2 - x_0, y_2 - y_0>) | \\ & = \dfrac{1}{2} * |(x_1 - x_0) * (y_2 - y_0) - (x_2 - x_0) * (y_1 - y_0) | \end{aligned}
a = 2 1 ∗ ∣ ( P 1 − P 0 ) × ( P 2 − P 0 ) ∣ = 2 1 ∗ ∣ ( < x 1 , y 1 > − < x 0 , y 0 > ) × ( < x 2 , y 2 > − < x 0 , y 0 > ) ∣ = 2 1 ∗ ∣ ( < x 1 − x 0 , y 1 − y 0 > ) × ( < x 2 − x 0 , y 2 − y 0 > ) ∣ = 2 1 ∗ ∣ ( x 1 − x 0 ) ∗ ( y 2 − y 0 ) − ( x 2 − x 0 ) ∗ ( y 1 − y 0 ) ∣
这里需要说明的一点是,二维向量实际上是没有叉积定义的,但是我们可以将二维坐标点看做是三维坐标点(第三维取 0 即可)来进行求解,更多细节还是请参看这里 .
讲到这里,我们便可以进行实现了,参考代码如下:
public struct Value2<T>
{
public float x;
public float y;
public T v;
public Vector2 Vector
{
get
{
return new Vector2(x, y);
}
}
public Value2(float x, float y, T v)
{
this.x = x;
this.y = y;
this.v = v;
}
}
public static float Cross(Vector2 v0, Vector2 v1)
{
return v0.x * v1.y - v1.x * v0.y;
}
public static float TriangleArea(Vector2 v0, Vector2 v1)
{
return 0.5f * Math.Abs(Cross(v0, v1));
}
public static float TriangleLerp(Value2f val0, Value2f val1, Value2f val2, Vector2 p)
{
var v01 = val1.Vector - val0.Vector;
var v02 = val2.Vector - val0.Vector;
var v0p = p - val0.Vector;
var a = TriangleArea(v01, v02);
Debug.Assert(a > 0, "[MathUtil]Error to do triangle Lerp, seems vertexes collinear ...");
var a0 = TriangleArea(v01, v0p);
var a1 = TriangleArea(v0p, v02);
var a2 = a - a0 - a1;
return (val2.v * a0 + val1.v * a1 + val0.v * a2) / a;
}
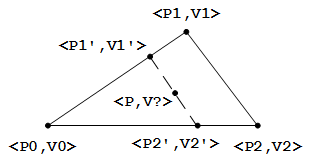
实际上我还尝试了一种类似于双线性插值 的求解方法,发现也是可行的,参考下图:
其中的虚线线段平行于向量 P2 - P1 (虚线取用其他线段也是可行的,只是计算上不方便),只要我们求解出 P1’ 的对应数值 V1’ , P2’ 的对应数值 v2’ ,以及子线段(P1’ 至 P )占总线段(P1’ 至 P2’ )的比例 t ,则 P 点对应的数值 V 便可以用简单的线性插值来求解了:
V
=
(
1
−
t
)
∗
V
1
′
+
t
∗
V
2
′
V = (1 - t) * V_1' + t * V_2'
V = ( 1 − t ) ∗ V 1 ′ + t ∗ V 2 ′
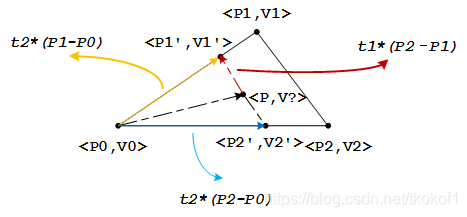
我们可以采用解析法来求解上面所需的 V1’ , V2’ 和 t , 参考下图:
我们设红色向量部分(P1’ - P )等于 t1 * (P2 - P1) ,黄色向量部分(P1’ - P0 )等于 t2 * (P1 - P0) ,由于相似三角形对应边成比例的关系,蓝色向量部分(P2’ - P0 )的比例系数也为 t2 ,类似的,向量 P2’ - P1’ 相对与向量 P2 - P1 的比例系数同样也为 t2 .
我们知道:
P
1
′
−
P
0
=
(
P
−
P
0
)
+
(
P
1
′
−
P
)
  
⟹
  
t
2
∗
(
P
1
−
P
0
)
=
(
P
−
P
0
)
+
t
1
∗
(
P
2
−
P
1
)
\begin{aligned} & P_1' - P_0 = (P - P_0) + (P_1' - P) \implies \\ & t_2 * (P_1 - P_0) = (P - P_0) + t_1 * (P_2 - P_1) \end{aligned}
P 1 ′ − P 0 = ( P − P 0 ) + ( P 1 ′ − P ) ⟹ t 2 ∗ ( P 1 − P 0 ) = ( P − P 0 ) + t 1 ∗ ( P 2 − P 1 )
并且 P0 的坐标为 <x0, y0> , P1 的坐标为 <x1, y1> , P2 的坐标为 <x2, y2> , P 的坐标为 <x, y>
则有:
{
t
2
∗
(
x
1
−
x
0
)
=
x
−
x
0
+
t
1
∗
(
x
2
−
x
1
)
t
2
∗
(
y
1
−
y
0
)
=
y
−
y
0
+
t
1
∗
(
y
2
−
y
1
)
\left\{ \begin{aligned} t_2 * (x_1 - x_0) & = x - x_0 + t_1 * (x_2 - x_1) \\ t_2 * (y_1 - y_0) & = y - y_0 + t_1 * (y_2 - y_1) \end{aligned} \right.
{ t 2 ∗ ( x 1 − x 0 ) t 2 ∗ ( y 1 − y 0 ) = x − x 0 + t 1 ∗ ( x 2 − x 1 ) = y − y 0 + t 1 ∗ ( y 2 − y 1 )
求解可得:
{
t
1
=
(
x
1
−
x
0
)
∗
(
y
−
y
0
)
−
(
x
−
x
0
)
∗
(
y
1
−
y
0
)
(
x
2
−
x
1
)
∗
(
y
1
−
y
0
)
−
(
x
1
−
x
0
)
∗
(
y
2
−
y
1
)
=
(
P
1
−
P
0
)
×
(
P
−
P
0
)
(
P
2
−
P
1
)
×
(
P
1
−
P
0
)
t
2
=
(
x
−
x
0
)
+
t
1
∗
(
x
2
−
x
1
)
x
1
−
x
0
o
r
(
y
−
y
0
)
+
t
1
∗
(
y
2
−
y
1
)
y
1
−
y
0
\left\{ \begin{aligned} t_1 & = \dfrac{(x_1 - x_0) * (y - y_0) - (x - x_0) * (y_1 - y_0)}{(x_2 - x_1) * (y_1 - y_0) - (x_1 - x_0) * (y_2 - y_1)} = \dfrac{(P_1 - P_0) \times (P - P_0)}{(P_2 - P_1) \times (P_1 - P_0)} \\ t_2 & = \dfrac{(x - x_0) + t_1 * (x_2 - x_1)}{x_1 - x_0} or \dfrac{(y - y_0) + t_1 * (y_2 - y_1)}{y_1 - y_0} \end{aligned} \right.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ t 1 t 2 = ( x 2 − x 1 ) ∗ ( y 1 − y 0 ) − ( x 1 − x 0 ) ∗ ( y 2 − y 1 ) ( x 1 − x 0 ) ∗ ( y − y 0 ) − ( x − x 0 ) ∗ ( y 1 − y 0 ) = ( P 2 − P 1 ) × ( P 1 − P 0 ) ( P 1 − P 0 ) × ( P − P 0 ) = x 1 − x 0 ( x − x 0 ) + t 1 ∗ ( x 2 − x 1 ) o r y 1 − y 0 ( y − y 0 ) + t 1 ∗ ( y 2 − y 1 )
可以看到 t1 的计算公式是一个叉积比例的形式,其实这个形式除了使用先前的解析方法,也可以运用几何方法来进行求解,只是对思维的要求比较高,有兴趣的朋友可以自己尝试一下(提示:叉积->面积).
有了 t1 和 t2 ,我们就可以计算之前的 V1’ , V2’ 和 t 了:
V
1
′
=
(
1
−
t
2
)
∗
V
0
+
t
2
∗
V
1
V
2
′
=
(
1
−
t
2
)
∗
V
0
+
t
2
∗
V
2
t
=
∣
t
1
∗
(
P
2
−
P
1
)
t
2
∗
(
P
2
−
P
1
)
∣
=
∣
t
1
t
2
∣
\begin{aligned} V_1' & = (1 - t_2) * V_0 + t_2 * V_1 \\ V_2' & = (1 - t_2) * V_0 + t_2 * V_2 \\ t &= | \dfrac{t_1 * (P_2 - P_1)}{t_2 * (P_2 - P_1)} | = |\dfrac{t_1}{t_2}| \end{aligned}
V 1 ′ V 2 ′ t = ( 1 − t 2 ) ∗ V 0 + t 2 ∗ V 1 = ( 1 − t 2 ) ∗ V 0 + t 2 ∗ V 2 = ∣ t 2 ∗ ( P 2 − P 1 ) t 1 ∗ ( P 2 − P 1 ) ∣ = ∣ t 2 t 1 ∣
相关实现代码如下:
public static float TriangleLerpV2(Value2f val0, Value2f val1, Value2f val2, Vector2 p)
{
var v01 = val1.Vector - val0.Vector;
var v12 = val2.Vector - val1.Vector;
var v0p = p - val0.Vector;
var c1 = Cross(v01, v0p);
var c2 = Cross(v12, v01);
Debug.Assert(c2 != 0, "[MathUtil]Error to do triangle Lerp, seems vertexes collinear ...");
var t1 = c1 / c2;
var t2 = v01.x != 0 ? (v0p.x + t1 * v12.x) / v01.x : (v0p.y + t1 * v12.y) / v01.y;
if (t2 == 0)
{
return val0.v;
}
else
{
var t3 = Math.Abs(t1 / t2);
var lerp0 = (1 - t2) * val0.v + t2 * val1.v;
var lerp1 = (1 - t2) * val0.v + t2 * val2.v;
return (1 - t3) * lerp0 + t3 * lerp1;
}
}
简单的测试对比发现,第二种插值方法较第一种快 10% 左右 ~