三元环枚举
BZOJ3498
N个点m条边,每个点有一个点权a。对于任意一个三元环(j,j,k)(i<j<k),它的贡献为max(ai,aj,ak)。求所有三元环的贡献和。
N<100000,m<250000。
题解
https://www.cnblogs.com/Khada-Jhin/p/10143074.html
三元环是一个不怎么常见的黑科技,它的求解方法是一种基于分块思想的方法,比较简单好写,在这里介绍一下三元环的计数方法及正确性与时间复杂度证明。
对于一个n个点m条边的无向图,三元环是指对于图上的三个点,两两点之间都直接有边相连,这三个点组成的环就是三元环。
三元环的计数方法:记录图中每个点的度数,对于每条边将它定向。对于一条边,将度数大的点指向度数小的点,如果度数相同就将编号小的点指向编号大的点。计数时枚举每个点,对于每个点x枚举它的出边,并将出边指向的点y打标记,对于所有出边指向的点y再枚举出边,如果这个出边指向的点z被打了标记,那么x,y,z就组成了一个三元环。时间复杂度为\(O(m\sqrt{m})\)。
对于这个方法只需要证明三点:
- 将边定向后的图是有向无环图(DAG)
这个很好证明,因为按照上述定向规则,我们称x连向y表示x比y大,那么任意两个点的大小关系是固定的,每个点只会向比它小的点连边,所以一定构成了有向无环图。
- 每个三元环只会被统计一次
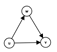
如图所示,因为三元环上的边是定向的,而且每个点只会枚举出边,所以每个三元环被统计的情况是唯一的。
3、时间复杂度为\(O(m\sqrt{m})\)
考虑时间复杂度分为两部分:一部分为每个点枚举出边,另一部分为每个出边指向的点枚举出边。
第一部分时间复杂度显然为O(n+m),而第二部分我们分类讨论:
如果一个点的出度大于\(\sqrt{m}\),指向它的点出度一定要比它大,这样的点最多\(\sqrt{m}\)个,时间复杂度为\(O(m\sqrt{m})\)。
如果一个点的出度小于\(\sqrt{m}\),指向他的点最多有n个,时间复杂度为\(O(n\sqrt{m})\)。
综上所述,时间复杂度为\(O(m\sqrt{m})\)。
CO int N=1e5+10;
int val[N],deg[N];
pair<int,int> E[3*N];
vector<int> to[N];
int vis[N];
int main(){
int n=read<int>(),m=read<int>();
for(int i=1;i<=n;++i) read(val[i]);
for(int i=1;i<=m;++i){
int u=read<int>(),v=read<int>();
E[i]={u,v};
++deg[u],++deg[v];
}
for(int i=1;i<=m;++i){
int u=E[i].first,v=E[i].second;
if(deg[u]<deg[v]) swap(u,v);
to[u].push_back(v);
}
int64 ans=0;
for(int u=1;u<=n;++u){
for(int v:to[u]) vis[v]=u;
for(int v:to[u])for(int w:to[v])if(vis[w]==u)
ans+=max(val[u],max(val[v],val[w]));
}
printf("%lld\n",ans);
return 0;
}代码里面没写度数相等时的连边方式竟然还是对的……
旧试题
计算如下表达式的值
\[ \Big(\sum_{i = 1}^{A}\sum_{j = 1}^{B}\sum_{k = 1}^{C} d(i j k) \Big) \bmod (10^9 + 7) \]
其中 \(d(i j k)\) 表示 \(i\times j\times k\) 的约数个数。
题解
https://www.cnblogs.com/cjyyb/p/10581730.html
首先有结论
\[ d(ijk)=\sum_{x|i}\sum_{y|j}\sum_{z|k}[\gcd(x,y)=1][\gcd(x,z)=1][\gcd(y,z)=1] \]
如何证明呢?可以分质因数考虑。
我们知道一个次数为 \(k\) 的质因数 \(p\) 的贡献是 \(k+1\)。而无论 \(i,j,k\) 分别含有多少个 \(p\),两两互质的 \(x,y,z\) 三元组的枚举刚好对应了 \(k+1\) 种方案。这样我们就证明了这个式子的正确性。
接着我们就可以把式子写成:
\[ \sum_{i=1}^A\sum_{j=1}^B\sum_{k=1}^C\sum_{x|i}\sum_{y|j}\sum_{z|k}[\gcd(x,y)=1][\gcd(y,z)=1][\gcd(z,x)=1] \]
然后改变枚举顺序:
\[ \sum_{x=1}^A\sum_{y=1}^B\sum_{z=1}^C[\gcd(x,y)=1][\gcd(y,z)=1][\gcd(z,x)=1]\left\lfloor\frac{A}{x}\right\rfloor\left\lfloor\frac{B}{y}\right\rfloor\left\lfloor\frac{C}{z}\right\rfloor \]
把 \([\gcd(x,y)=1]\) 变成 \(\sum_{d|x,d|y}\mu(d)\),然后式子就变成了:
\[ \sum_{x=1}^A\sum_{y=1}^B\sum_{z=1}^C\sum_{i|x,i|y}\sum_{j|y,j|z}\sum_{k|z,k|x}\mu(i)\mu(j)\mu(k)\left\lfloor\frac{A}{x}\right\rfloor\left\lfloor\frac{B}{y}\right\rfloor\left\lfloor\frac{C}{z}\right\rfloor \]
然后转而枚举 \(i,j,k\):
\[ \sum_{i=1}^A\sum_{j=1}^B\sum_{k=1}^C\mu(i)\mu(j)\mu(k)\sum_{\mathrm{lcm}(i,k)|x}\left\lfloor\frac{A}{x}\right\rfloor\sum_{\mathrm{lcm}(i,j)|y}\left\lfloor\frac{B}{y}\right\rfloor\sum_{\mathrm{lcm}(j,k)|z}\left\lfloor\frac{C}{z}\right\rfloor \]
后面的东西,显然可以在调和级数的复杂度内预处理,并且当 \(\mathrm{lcm}>\max\{A,B,C\}\) 的时候的值就是 \(0\)。
那么考虑枚举两个数,如果它们两个的 \(\mathrm{lcm}\leq \max\) 的话就在他们之间连上一条边,这样子就得到了一张无向图,每一个三元环把他们对应到 \(i,j,k\) 上面就是一组解。
另外特殊处理一下 \(i,j,k\) 中有两个相同的或者三个都相同的情况。
然而直接枚举任意两个点建边是 \(O(n^2)\) 的。
我们考虑枚举两者的 \(\gcd\),然后再来枚举两个互质的数,因为 \(\mu=0\) 也是没有贡献的,所以 \(\mu=0\) 的数也不用考虑,这样子就可以减掉大量没有用的状态。
然后跑个三元环就好了。
CO int N=1e5+10,mod=1e9+7;
int pri[N],tot,mu[N];
int64 fa[N],fb[N],fc[N];
struct edge {int u,v,w;};
vector<edge> E,to[N];
int deg[N],vis[N],book[N];
void real_main(){
int A=read<int>(),B=read<int>(),C=read<int>();
int n=max(A,max(B,C));
for(int i=1;i<=A;++i)for(int j=i;j<=A;j+=i) fa[i]+=A/j;
for(int i=1;i<=B;++i)for(int j=i;j<=B;j+=i) fb[i]+=B/j;
for(int i=1;i<=C;++i)for(int j=i;j<=C;j+=i) fc[i]+=C/j;
int64 ans=0;
for(int i=1;i<=min(A,min(B,C));++i) ans+=mu[i]*fa[i]*fb[i]*fc[i]; // (i,i,i)
for(int i=1;i<=n;++i)if(mu[i])
for(int j=1;i*j<=n;++j)if(mu[i*j])
for(int k=j+1;(int64)i*j*k<=n;++k)if(mu[i*k] and __gcd(j,k)==1){
int x=i*j,y=i*k,l=i*j*k;
ans+=mu[y]*(fa[x]*fb[l]*fc[l]
+fa[l]*fb[x]*fc[l]+fa[l]*fb[l]*fc[x]); // (x,x,y)
ans+=mu[x]*(fa[y]*fb[l]*fc[l]
+fa[l]*fb[y]*fc[l]+fa[l]*fb[l]*fc[y]); // (y,y,x)
E.push_back({x,y,l});
++deg[x],++deg[y];
}
for(CO edge&e:E){
int u=e.u,v=e.v;
if(deg[u]<deg[v] or (deg[u]==deg[v] and u<v)) swap(u,v);
to[u].push_back({u,v,e.w});
}
for(int i=1;i<=n;++i){
for(CO edge&e:to[i]) vis[e.v]=i,book[e.v]=e.w;
for(CO edge&e:to[i]){
int u=e.v,a=e.w;
for(CO edge&e:to[u])if(vis[e.v]==i){
int v=e.v,b=e.w,c=book[v];
ans+=mu[i]*mu[u]*mu[v]*(fa[a]*fb[b]*fc[c]+fa[a]*fb[c]*fc[b]
+fa[b]*fb[a]*fc[c]+fa[b]*fb[c]*fc[a]
+fa[c]*fb[a]*fc[b]+fa[c]*fb[b]*fc[a]); // (i,u,v)
}
}
}
printf("%lld\n",ans%mod);
// clear
fill(fa+1,fa+n+1,0),fill(fb+1,fb+n+1,0),fill(fc+1,fc+n+1,0);
E.clear();
fill(deg+1,deg+n+1,0);
for(int i=1;i<=n;++i) to[i].clear();
fill(vis+1,vis+n+1,0);
}
int main(){
mu[1]=1;
for(int i=2;i<N;++i){
if(!pri[i]) pri[++tot]=i,mu[i]=-1;
for(int j=1;j<=tot and i*pri[j]<N;++j){
pri[i*pri[j]]=1;
if(i%pri[j]==0){
mu[i*pri[j]]=0;
break;
}
mu[i*pri[j]]=-mu[i];
}
}
for(int T=read<int>();T--;) real_main();
return 0;
}