斜率优化入门
先看一下题意
将n个任务在一台机器上分批加工,每批包含相邻若干任务,从0时刻开始,加工这些任务,其中第i个任务加工时间为 ti。在每批任务开始前,机器需要启动时间s,完成这批任务需要的时间是各个任务需要的时间和(同一批任务会在同一时刻完成)。每个任务的费用是他完成时刻乘一个费用系数 ci 。确定一个分组方案,使得总费用最小。
解析
经过思考,这个题大致是一个DP题,那既然是DP题,它的状态转移方程是怎样的呢?
我们定义 \(f[i]\) 为处理前 i 个任务的最小花费。
假如已知 \(f[1]\) ~ \(f[i-1]\) 如何求 \(f[i]\) 呢?
如果我们决定先处理前 j 个任务,那么 j+1 ~ i 这些任务将放在一批处理。
此时 \(f[i] = f[j] + ((k+1)*s + \sum_{l=1}^{i}t[l])*(\sum_{l=j+1}^if[l])\) 其中 k 是前 j 个任务分了 k 批。
所以我们只要遍历 j ,找到最优的状态来转移即可。
但是我们发现由于 k 的存在,状态转移方程不是很方便使用,于是我们采用费用提前的思想
什么是费用提前呢,就是在处理之前的任务时,把s产生的费用提前计算了。
那么最后的方程如下
\[ f[i] = min(f[j]+(\sum_{l=1}^it[l])*\sum_{l=j+1}^ic[l]+s*\sum_{l=j+1}^nc[l]) \]将 \(t,c\) 表示成其对应的前缀和。
\[ f[i] = min(f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j])) \]
qwq,以为写出状态转移方程就结束了吗?不不不,现在才刚刚开始进入正题!
对于\(dp[i] = dp[j] + f[j]*g[i] + h[i]\)这类DP,我们可以用斜率优化来处理。
令 \(j,k(j>k)\) ,此时,从 j 转移更优
所以
\[ f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j]) < f[k]+t[i]*(c[i]-c[k])+s*(c[n]-c[k]) \]化简一下
\[ f[j]-f[k] < (t[i]+s)*(c[j]-c[k]) \]
\[ \frac{f[j]-f[k]}{c[j]-c[k]} < t[i]+s \]
- 有没有觉得这个式子有斜率的感觉!
- 我们将 \((c[i],f[i])\) 这些点在坐标轴上表示
- 由于 c 为前缀和,故 c 是单调递增的。
- 入图所示
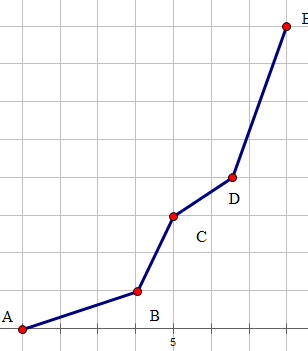
- 拿出 B,C,D三个点分析,发现 \(\frac{f[D]-f[C]}{c[D]-c[C]} < \frac{f[C]-f[B]}{c[C]-c[B]}\)
- 当 一个斜率如图所示时 (\(t[i] + s\) 即是斜率)
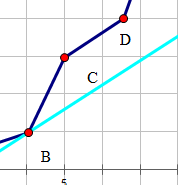
- 此时的最优转移点是 B 点,因为 t 也是前缀和,所以 t 也是单调递增的,当 斜率增大时
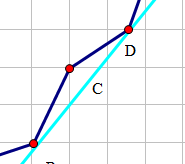
- 最优转移点逐渐从 B 点变成 D 点,这时候我们发现 C 点就完全无用了,可以删除。
- 所以就变成了维护一个下凸包,两点之间的斜率是逐渐递增的。
- 由于 t 也是递增的,所以我们用一个单调队列来维护这个下凸包的点集
- 当队首及其下一个点所构成直线的斜率比当前斜率(\(t[i]+s\))要小时,将队首出队(这一操作不断进行)
- 最后队首即为最优转移点!
- 接下来要将 i 点入队,我们要保证单调队列里面是一个下凸包的点集,所以 i 点与队尾所构成的直线的斜率要比 队尾与队尾前一个点 的斜率要大,若不满足则队尾要不断出队。
这时候我们就成功用一个单调队列来维护这个点集辣。
小提示
- 如果 t 不保证递增 (戳这里两个题的唯一区别就在,这个题的 t 可以是负数qwq,所以前缀和不是递增的),这时候我们维护的下图包的需要二分来找到最优解。
放代码QwQ
#include<bits/stdc++.h> #define int long long using namespace std; const int Maxn = 5050; int n,s; int t[Maxn],f[Maxn],dp[Maxn]; int q[Maxn]; // 我们所维护的 单调队列 // 这部分是分子上的式子 int Up(int j,int k){ return dp[j] - dp[k]; } // 这部分是分母所对应的式子 int Down(int j,int k){ return f[j] - f[k]; } // 这部分是找到 i 的最优转移点 j 后,求出 dp[i] 的值 int DP(int i,int j){ return dp[j] + t[i]*(f[i]-f[j]) + s*(f[n]-f[j]); } signed main(){ scanf("%lld %lld",&n,&s); for(int i=1;i<=n;i++) scanf("%lld %lld",&t[i],&f[i]),t[i]+=t[i-1],f[i]+=f[i-1]; int head = 1,tail = 1; // 单调队列的队首和队尾 q[tail++] = 0; for(int i=1;i<=n;i++) { // 如果队首及其下一个点所构成直线的斜率比 t[i]+s 小 则队首出队 while( head+1 < tail && Up(q[head+1],q[head]) <= (t[i]+s)*Down(q[head+1],q[head]) ) head++; dp[i] = DP(i,q[head]); // 现在要将 i 点放进单调队列 由于必须保证单调队列里面是一个下凸包 所以把不满足的队尾出队 while( head+1 < tail && Up(i,q[tail-1])*Down(q[tail-1],q[tail-2]) <= Up(q[tail-1],q[tail-2])*Down(i,q[tail-1]) ) tail--; q[tail++] = i; } // 终于输出答案辣 qwq cout<<dp[n]<<endl; return 0; }