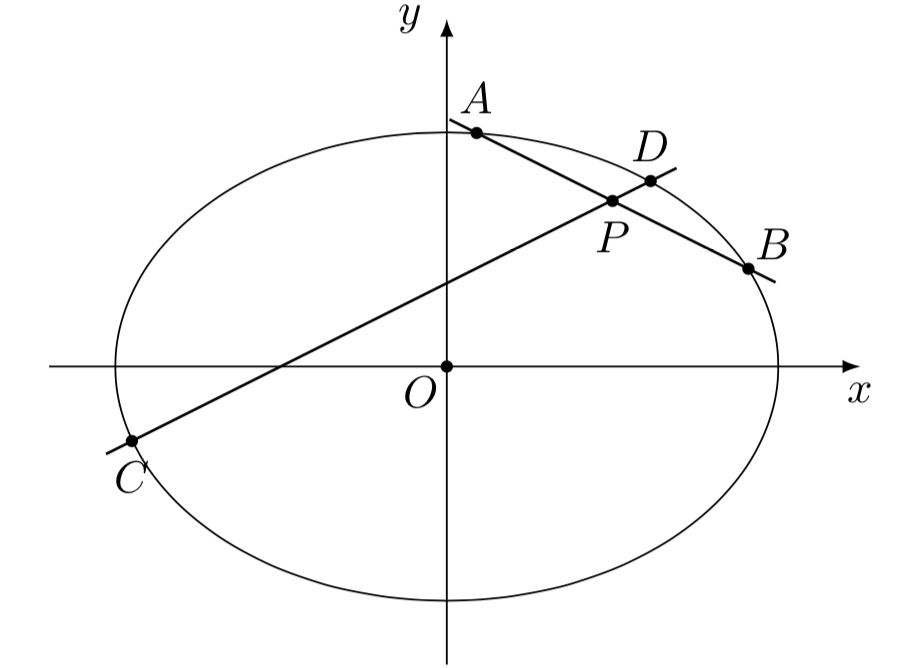
已知椭圆\(\mathit{\Gamma}: \dfrac{x^2}{4}+\dfrac{y^2}{2}=1\),过点\(P(1,1)\)作倾斜角互补的两条不同直线\(l_1,l_2\),设\(l_1\)与椭圆\(\mathit{\Gamma}\)交于\(A,B\)两点,\(l_2\)与椭圆\(\mathit{\Gamma}\)交于\(C,D\)两点.
\((1)\) 若\(P(1,1)\)为线段\(AB\)的中点,求直线\(AB\)的方程;
\((2)\) 记\(\lambda=\dfrac{|AB|}{|CD|}\),求\(\lambda\)的取值范围.
解析:
\((1)\) 法一 若记\(P(x_0,y_0)\),则当\(P\)为弦\(AB\)的中点时,由中点弦方程可得直线\(AB\)方程为\[ \dfrac{x_0x}{4}+\dfrac{y_0y}{2}=\dfrac{x_0^2}{4}+\dfrac{y_0^2}{2}.\]因此所求直线方程为\(x+2y-3=0\).
法二 由题显然\(AB\)的斜率存在,设点\(Q(x,y)\)是直线\(AB\)上任意一个异于\(P\)点的的点,则由椭圆的垂径定理知\(OP\)直线的斜率与\(PQ\)直线的斜率乘积为\(-\dfrac{b^2}{a^2}\),其中\(a,b\)分别为椭圆的半长轴,半短轴.即有\[ \dfrac{y-1}{x-1}\cdot \dfrac{1-0}{1-0}=-\dfrac{2}{4}.\]又即\(x+2y-3=0\).
\((2)\) 由题,设\(l_1\)的倾斜角为\(\theta\),则\(l_2\)的倾斜角为\(\pi-\theta\),其中\(\theta\)的取值范围为
\(\left(0,\dfrac{\pi}{2}\right)\cup\left(\dfrac{\pi}{2},\pi\right)\).于是直线 \(AB\)的参数方程为
\[ \begin{cases} & x=1+t\cos\theta,\\ & y=1+t\sin\theta, \end{cases} (t\text{是参数}). \]
将以上参数方程代入椭圆方程并整理可得 \[ \left(\dfrac{\cos^2\theta}{4}+\dfrac{\sin^2\theta}{2}\right)\cdot t^2+\left(\dfrac{1}{2}\cos\theta+\sin\theta\right)\cdot t-\dfrac{1}{4}=0.\]若记 \(A,B\)两点对应的参数分别为 \(t_1,t_2\),则 \[ \begin{split} |AB|&=|t_1-t_2|\\ &=\dfrac{\sqrt{\left(\dfrac{1}{2}\cos\theta+\sin\theta\right)^2-4\cdot\left(-\dfrac{1}{4}\right)\cdot \left(\dfrac{\cos^2\theta}{4}+\dfrac{\sin^2\theta}{2}\right)}}{\dfrac{\cos^2\theta}{4}+\dfrac{\sin^2\theta}{2}}\\ &=f(\theta). \end{split} \]则
\[ \begin{split} \lambda&=\dfrac{|AB|}{|CD|}\\ &=\dfrac{f(\theta)}{f\left(\pi-\theta\right)}\\ &=\sqrt{\dfrac{\cos^2\theta+3\sin^2\theta+2\sin\theta\cos\theta}{\cos^2\theta+3\sin^2\theta-2\sin\theta\cos\theta}}\\ &=\sqrt{1+\dfrac{4\tan\theta}{3\tan^2\theta-2\tan\theta+1}}. \end{split} \]由于 \(\theta\)的取值范围为 $ \left(0,\dfrac{\pi}{2}\right)\cup\left(\dfrac{\pi}{2},\pi\right)$ ,所以 \(\lambda\)的取值范围为 \(\left[\dfrac{\sqrt{6}-\sqrt{2}}{2},1\right)\cup\left(1,\dfrac{\sqrt{6}+\sqrt{2}}{2}\right]\).