我们知道，对于ap（p>0）的求值，朴素的求幂算法采用递推的方式，即将底数a累乘指数p次作为结果。这种算法的时间复杂度为O(p)，当指数p很大（>1e7）时，即便该算法拥有线性时间复杂度，在当下的机器上仍需要花大量的运算时间。
因此需要对朴素幂算法进行改进，一种高效的方式是分治：当p为偶数时，直接将ap分为(ap/2)*(ap/2)两部分，而每个ap/2又可做继续划分，直到成为1次幂；当p为奇数时，我们提出一个a，则剩下的ap-1就变为了偶指数形式，回到前述情况；当指数为0时，可以很容易得出结果为1。最后再将每步分出的结果合并即可。由此我们可以写出递归式的数学表达：
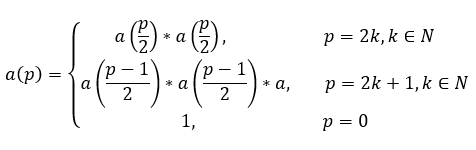
分治解法的时间复杂度为O(log p)，这个结果相比线性复杂度而言有了很大提升，例如当指数p=18,446,744,073,709,551,616时，只需计算64次乘法即可得出结果。
如何实现这个算法呢？首先会想到递归地处理这个问题：注意对于较大的运算结果，应考虑高精度模拟运算，或者考虑本文末尾的模m算法。
typedef long long ll; ll fspow(ll a, ll p) { if(p==0) return 1; if(p&1) { ll t = fspow(a, p-1); return t*a; } else { ll t = fspow(a, p/2); return t*t; } }
很多人对递归有一种直觉上的抵触，认为递归效率不高。实际并不总是如此。我们知道函数调用的时间开销主要体现在两个方面：1、调用栈会保存函数的形参、局部变量、返回地址等信息，这需要由高延迟的访存指令来实现；2、分支指令会造成额外的开销，例如由于分支预测失效造成的流水线冲刷等等。
但事实是，若数据规模很大时，相比于不小心把原本O(log p)的算法活生生地写成O(p)的算法造成的浪费而言，这些由系统底层造成的开销是微不足道的。除非你所面临的是资源非常有限的系统，或者你想通过极限优化来卡数据，否则不必在意递归调用的时间开销。当然必须考虑递归的空间复杂度。
递归算法会增长地占用栈空间，这一点是我们所不希望看到的。能否有一种既能保持简洁优雅，又能拥有常数空间复杂度的快速幂算法呢？
这就是快速幂算法的非递归版本。下面这两行代码已经将核心浓缩到了极致：
1 for (s=1; p;p/=2,a=a*a) 2 if (p&1) s=s*a;
其中a为底数，p为指数，算法结束后，s=ap。
再来看算法的原理。思路仍是分治，这与我们之前的讨论是一致的，不同的是不再递归地求解。
“分”的本质是使指数折半，这里指数必须为偶数。当指数折半后，要使幂结果不变，底数必须平方。形式化描述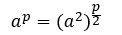
。而指数p/2又可继续分为p/4 p/8……1，底数则不断累乘。指数将为1时，底数即为要求的结果。当指数不是偶数时，先拆出一个底数，则剩下的幂就是偶次幂，再按如上方法处理即可。
代码中涉及一些小技巧：
1. 利用了整除算符/的向下取整特性。当指数p为奇数时，p/2的结果实质上等同于p-1/2，这就免去了当我们拆出一个底数时需要把p减一的麻烦。事实上，由于除数为2，也可以写成p>>=1，本质上利用了二进制除法。
2. 我们知道%运算符的开销是很大的，这里只需判断p的奇偶性，直接判断p的二进制最低位即可。
具体应用
幂运算在许多场合都有着重要的运用。例如RSA非对称加密算法中，明文通过如下公式进行加密：
Ci = Mie mod n
其中Ci为密文，Mi为与明文有关的数值，(e, n)为公钥对。
而密文通过如下公式解密：
Mi = Cid mod n
其中Mi为与明文有关的数值，(d, n)为私钥对。
可以看到，无论是加密还是解密，都要用到幂运算与模运算。这就与我们上文所述的快速幂运算很有关联。
不止RSA，在其它运用中也常常出现类型的形式，它们归结下来如下面这个式子：
ap mod k
由于幂结果取模，最终结果并不会大于等于k。再看看我们的快速幂算法，中间结果很可能远大于k，如果中间结果超出基本数据类型的范围，还需要通过高精度模拟运算，这是没有必要而且浪费时间的。所以上文的快速幂算法还有优化的余地。
数论指出，(a*b) mod k = (a mod k)*(b mod k) mod k。即两个数的乘积再取模，等于两个数分别取模再相乘，并取模。利用这个性质，我们可以将ap mod k等价变形为(a mod k)p mod k，同时每次做乘法时，都先利用该性质缩小乘数，再相乘。
上述代码修改为
1 a %= k; 2 for (s=1; p;p/=2,a=(a*a)%k) 3 if (p&1) s=(s*a)%k;
其中a，p，k，s的含义与上文一致。
这便是快速幂模k算法的非递归实现。