SPOJ GSS系列解题报告

其他 2019-10-25 12:01:02 阅读次数: 0

众所周知，\(GSS\)是用来练习线段树的一个非常好的系列。

依稀记得\(8\)月初还在\(qbxt\)时，某钟姓神仙说过 :“大家可以把\(GSS\)系列写一下，大概够大家写一个月了。”虽然我很不想承认，但他确实说中了\(……\)虽然中间夹有做各种杂题和一些模拟赛\(……\)

题解

GSS 1

\(GSS\)系列最简单的一道题，也算是后面题目的一个基础。

给定一个序列，维护区间最大子段和。

我们维护这样几个东西\(:lsum, rsum, maxsum, maxval.\)

分别表示区间最大前缀和，区间最大后缀和，区间最大子段和，区间最大值，其中最大前缀和与最大后缀和用于辅助求出最大子段和。

我们考虑一下如何合并左右两个区间：

  • 对于当前区间的\(lsum\),我们取左区间的\(lsum\)和左区间的\(sum+\)右区间的\(lsum\)中的最大值来更新。
  • 对于当前区间的\(rsum\)，我们采取与维护\(lsum\)相似的方式维护，取右区间的\(rsum\)和左区间的\(lsum+\)右区间的\(sum\)中的最大值来更新。
  • 对于当前区间的\(maxsum\)，即最大子段和，我们取左区间的\(maxsum\)和右区间的\(maxsum\)和左区间的\(rsum+\)右区间的\(lsum\)中的最大值来更新当前区间的\(maxsum\)。
  • 对于当前区间的\(maxval\)，正常维护即可。之所以要维护\(maxval\),是因为当我们发现要询问的区间的最大值小于0时，直接输出当前区间的\(maxval\)即可。

另外，关于最大子段和，版本不同对于最大子段和是否可以为空要求不同，所以代码细节可能会比较多，对于像我一样粗心的人可能会不太友好\(……\)

code:

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 5e4 + 5;
int w, ch, n, m, a[maxn];

template<class T>
T read(T &x)
{
    x = 0, w = 1, ch = getchar();
    while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}
    return x *= w;
}

struct node {
    int l, r, maxsum, sum, maxval;
    int fmax, bmax;
}z[maxn << 2];

node operator + (const node &a, const node &b)
{
    node ans;
    ans.l = a.l;
    ans.r = b.r;
    ans.sum = a.sum + b.sum;
    ans.maxval = max(a.maxval, b.maxval);
    ans.maxsum = max(a.maxsum, max(b.maxsum, a.bmax + b.fmax));
    ans.fmax = max(a.fmax, a.sum + b.fmax);
    ans.bmax = max(b.bmax, b.sum + a.bmax);
    return ans;
}

void pushup(int rt)
{
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

void build(int rt, int l, int r)
{
    if (l == r) {
        z[rt].l = l, z[rt].r = r;
        z[rt].sum = z[rt].maxval = a[l];
        if (z[rt].sum < 0) {
            z[rt].maxsum = z[rt].fmax = z[rt].bmax = 0;
        }
        else {
            z[rt].maxsum = z[rt].fmax = z[rt].bmax = a[l];
        }
        return ;
    }
    int mid = (l + r) >> 1;
    build (rt << 1, l, mid);
    build (rt << 1 | 1, mid + 1, r);
    pushup(rt);
}

node query(int rt, int l, int r)
{
    if (z[rt].l == l && z[rt].r == r)
        return z[rt];
    int mid = (z[rt].l + z[rt].r) >> 1;
    if (r <= mid)
        return query(rt << 1, l, r);
    if (l > mid)
        return query(rt << 1 | 1, l, r);
    return query(rt << 1, l, mid) + query(rt << 1 | 1, mid + 1, r);
}

int main()
{
    read(n);
    for (int i = 1; i <= n; i++) read(a[i]);
    build(1, 1, n);
    read(m);
    int L, R;
    while (m--) {
        read(L), read(R);
        node ans = query(1, L, R);
        if (ans.maxval < 0) cout << ans.maxval << '\n';
        else cout << ans.maxsum << '\n';
    }
    return 0;
}

GSS 2

讲道理，窝\(jio\)得这是\(GSS\)系列中最难的一道题，所以窝也不知道为什么这道题会放在第二位。

看题面，我们会发现这道题仅仅比\(GSS 1\)多了一个判重的操作，然后\(……\)他的难度就上天了！！

遇到这种需要去重的问题，我们采取一个比较套路的方法：离线。

没错！！这是一道离线神题！！

考虑到我们需要去重，\(GSS1\)中用到的记录区间前缀，后缀的方法就不再适用了，所以我们需要一棵很强的线段树来维护一些很强的东西！！

先说思路和做法，对于本题我们维护的线段树，线段树的叶子结点\(j\)表示\(j\)到当前节点\(i\)这个区间的最大子段和，即\(:\)

\(max\{A[l]+A[l+1]+……+A[r]\}\) 其中 \(j \leq l \leq r \leq i\)

我们维护这样几个东西\(:\)当前区间最大子段和\(maxsum\)，区间历史最大子段和\(hismaxsum\)，懒标记\(tag\)，历史最大懒标记\(histag\)

我们将所有的询问按照右端点排序，每次将一个数插入线段树中，仔细思考一下，我们更新之前每一个节点，其实就是在进行一个区间加的过程，但我们需要去重，一个简便的方法\(:\)记录一个\(pre[a[j]]\)来记录\(a[j]\)前一次出现的位置，这样我们每次修改\(\{pre[a[j]]+1, i\}\)即可避免\(a[j]\)对之前造成影响，当我们当前节点与询问的右端点相同时，即可更新并记录答案，更新答案时我们发现，当前的\(maxsum\)不一定是最大子段和，而\(hismaxsum\)才是，原因是显然的。

代码细节\(:\)

  • 在进行\(pushdonw\)时，对于子区间的\(hsimaxsum\)和\(histag\)直接下放当前区间的\(histag\)，原因和更新答案的原理是相似的。

  • 在向线段树中插入时，要注意更新的顺序，先更新\(maxsum\)和\(tag\)，再更新\(hismaxsum\)和\(histag\)，这样就保证了区间的连续性。

  • 剩下就是一些细节要注意，例如记录\(pre\)数组时，为防止出现负下标，把每个数整体向后移100000位\(……\)

code：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long

namespace LXC
{
    template<class T>
    inline T read(T &x)
    {
        x = 0; int w = 1, ch = getchar();
        while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
        while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}
        return x *= w;
    }

    template<class T>
    inline T max(const T a, const T b)
    {
        return a > b ? a : b;
    }
}
using namespace LXC;
using std::sort;

const int maxn = 2e5 + 5;
int n, m, a[maxn], pre[maxn << 1];
int x[maxn], y[maxn], idx[maxn];

bool cmp(int a, int b)
{
    return y[a] < y[b];
}

struct Node {
    int l, r;
    ll maxsum, maxsum_old; // 当前贡献最大值   从开始到现在历史贡献最大值
    ll tag, tag_old; // 懒标记 从上次pushdown到现在最大懒标记
}z[maxn << 2], ans[maxn];

Node operator + (const Node &a, const Node &b)
{
    Node ans;
    ans.l = a.l;
    ans.r = b.r;
    ans.maxsum = max(a.maxsum, b.maxsum);
    ans.maxsum_old = max(a.maxsum_old, b.maxsum_old);
    ans.tag = ans.tag_old = 0;
    return ans;
}

void pushdown(int rt)
{
    int ls = rt << 1, rs = rt << 1 | 1;
    ll v_old = z[rt].tag_old, v = z[rt].tag;
    z[ls].maxsum_old = max(z[ls].maxsum_old, z[ls].maxsum + v_old);
    z[ls].tag_old = max(z[ls].tag_old, z[ls].tag + v_old);
    z[ls].maxsum += v;
    z[ls].tag += v;
    z[rs].maxsum_old = max(z[rs].maxsum_old, z[rs].maxsum + v_old);
    z[rs].tag_old = max(z[rs].tag_old, z[rs].tag + v_old);
    z[rs].maxsum += v;
    z[rs].tag += v;
    z[rt].tag = z[rt].tag_old = 0;
}

void modify(int rt, int L, int R, int l, int r, ll w)
{
    if (L <= l && r <= R) {
        z[rt].maxsum += w, z[rt].maxsum_old = max(z[rt].maxsum_old, z[rt].maxsum);
        z[rt].tag += w, z[rt].tag_old = max(z[rt].tag_old, z[rt].tag);
        return ;
    }
    int mid = (l + r) >> 1;
    pushdown(rt);
    if (L <= mid)
        modify(rt << 1, L, R, l, mid, w);
    if (R > mid)
        modify(rt << 1 | 1, L, R, mid + 1, r, w);
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

Node query(int rt, int L, int R, int l, int r)
{
    if (L <= l && r <= R) return z[rt];
    int mid = (l + r) >> 1;
    pushdown(rt);
    if (R <= mid)
        return query(rt << 1, L, R, l, mid);
    if (L > mid)
        return query(rt << 1 | 1, L, R, mid + 1, r);
    return query(rt << 1, L, R, l, mid) + query(rt << 1 | 1, L, R, mid + 1, r);
}

int main()
{
    read(n);
    for (int i = 1; i <= n; i++) read(a[i]);
    read(m);
    for (int i = 1; i <= m; i++) {
        read(x[i]), read(y[i]);
        idx[i] = i;
    }
    sort(idx + 1, idx + m + 1, cmp);
    int j = 1;
    for (int i = 1; i <= n; i++) {
        modify(1, pre[a[i] + 100000] + 1, i, 1, n, a[i]);
        pre[a[i] + 100000] = i;
        while (y[idx[j]] == i && j <= m) ans[idx[j]] = query(1, x[idx[j]], y[idx[j]], 1, n), j++;
    }
    for (int i = 1; i <= m; i++) printf("%lld\n", ans[i].maxsum_old);
    return 0;
}

GSS 3

没什么可说的，依旧是查询最大子段和，只比\(GSS1\)多了一个单点修改。

当然，单点修改对于我们的维护是没有任何影响的，但如果是区间修改\(……\)标记的下放可能会比较恶心，有时间可以考虑一下。

code：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int maxn = 5e4 + 5;
int w, ch, n, m, a[maxn];

template<class T>
T read(T &x)
{
    x = 0, w = 1, ch = getchar();
    while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}
    return x *= w;
}

struct node {
    int l, r, maxsum, sum, maxval;
    int fmax, bmax;
}z[maxn << 2];

node operator + (const node &a, const node &b)
{
    node ans;
    ans.l = a.l;
    ans.r = b.r;
    ans.sum = a.sum + b.sum;
    ans.maxval = max(a.maxval, b.maxval);
    ans.maxsum = max(a.maxsum, max(b.maxsum, a.bmax + b.fmax));
    ans.fmax = max(a.fmax, a.sum + b.fmax);
    ans.bmax = max(b.bmax, b.sum + a.bmax);
    return ans;
}

void pushup(int rt)
{
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

void build(int rt, int l, int r)
{
    if (l == r) {
        z[rt].l = l, z[rt].r = r;
        z[rt].sum = z[rt].maxval = a[l];
        if (z[rt].sum < 0) {
            z[rt].maxsum = z[rt].fmax = z[rt].bmax = 0;
        }
        else {
            z[rt].maxsum = z[rt].fmax = z[rt].bmax = a[l];
        }
        return ;
    }
    int mid = (l + r) >> 1;
    build (rt << 1, l, mid);
    build (rt << 1 | 1, mid + 1, r);
    pushup(rt);
}

void modify(int rt, int x, int y)
{
    if (z[rt].l == z[rt].r) {
        if (y < 0){
            z[rt].maxsum = z[rt].fmax = z[rt].bmax = 0;
            z[rt].sum = z[rt].maxval = y;
        }
        else
            z[rt].sum = z[rt].maxval = z[rt].maxsum = z[rt].fmax = z[rt].bmax = y;
        return ;
    }
    int mid = (z[rt].l + z[rt].r) >> 1;
    if (x <= mid)
        modify(rt << 1, x, y);
    else
        modify(rt << 1 | 1, x, y);
    pushup(rt);
}

node query(int rt, int l, int r)
{
    if (z[rt].l == l && z[rt].r == r)
        return z[rt];
    int mid = (z[rt].l + z[rt].r) >> 1;
    if (r <= mid)
        return query(rt << 1, l, r);
    if (l > mid)
        return query(rt << 1 | 1, l, r);
    return query(rt << 1, l, mid) + query(rt << 1 | 1, mid + 1, r);
}

int main()
{
    read(n);
    for (int i = 1; i <= n; i++) read(a[i]);
    build(1, 1, n);
    read(m);
    int opt, L, R;
    while (m--) {
        read(opt), read(L), read(R);
        if (opt == 0)
            modify(1, L, R);
        else {
            node ans = query(1, L, R);
            if (ans.maxval < 0) cout << ans.maxval << '\n';
            else cout << ans.maxsum << '\n';
        }
    }
    return 0;
}

GSS 4

两个操作\(:\)区间开方，区间求和。

区间求和是很常规的操作，我们暂不考虑。

来看这个比较难搞的区间开方操作，很容易就可以想到对一个区间的\(sum\)进行开方，但我们仔细一想，开方和与和开方是肯定不一样的，所以我们\(……\)暴力来搞。

仔细算一下，一个\(10^{18}\)级别的数，只要对其开方六次，他就会变成\(1\)，我们就可以不再对它进行开方，这样就省去了大量的冗余操作，时间复杂度上限\(O(6 * 10^5)\)，这是可以接受的。

需要一提的是，这道题目是多组测试数据。不过它好像没什么数组需要清空……

code:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#define LL long long

using namespace std;

const int maxn = 1000005;

LL L[maxn<<2], R[maxn<<2], a[maxn<<2], tag[maxn<<2], sum[maxn<<2], ans;
int n, m;

void pushup(int rt)
{
    sum[rt] = sum[rt<<1] + sum[rt<<1|1];
    tag[rt] = tag[rt<<1] && tag[rt<<1|1];
}

void build(int rt,int l,int r)
{
    L[rt] = l, R[rt] = r;
    if (l == r) {
        sum[rt] = a[l];
        if (a[l] == 1) tag[rt] = 1;
        else tag[rt] = 0;
        return ;
    }
    int mid = (l+r) >> 1;
    build (rt << 1, l, mid);
    build (rt << 1 | 1, mid + 1, r);
    pushup(rt);
}

void modify(int rt, int l, int r)
{
    if (tag[rt]) return ;
    if (L[rt] == R[rt]) {
        sum[rt] = (LL)(sqrt(sum[rt]));
        if (sum[rt] <= 1)
            tag[rt] = 1;
        return ;
    }
    int mid = (L[rt] + R[rt]) >> 1;
    if (r <= mid)
        modify(rt << 1, l, r);
    if (l > mid)
        modify(rt << 1 | 1, l, r);
    if (l <= mid && r > mid) {
        modify(rt << 1, l, mid);
        modify(rt << 1 | 1, mid + 1, r);
    }
    pushup(rt);     
}

LL query(int rt, int l, int r)
{
    if (L[rt] == l && R[rt] == r) return sum[rt];
    int mid = (L[rt] + R[rt]) >> 1;;
    if (r <= mid)
        return query(rt << 1, l, r);
    if (l > mid)
        return query(rt << 1 | 1, l, r);
    return query(rt << 1, l, mid) + query(rt << 1 | 1, mid + 1, r);     
}
int main()
{
    int Case = 0;
    while (scanf("%d", &n) != EOF) {
        printf("Case #%d:\n",++Case);
        for (int i = 1; i <= n; i++) cin >> a[i];
        build (1, 1, n);
        scanf("%d", &m);
        int opt, x, y, i = 1;
        while (m--) {
            scanf("%d", &opt);
            if (opt == 0) {
                scanf("%d%d", &x, &y);
                if (x > y) swap(x, y); 
                modify(1, x, y);
            }
            else {
                scanf("%d%d", &x, &y);
                if(x > y) swap(x, y);
                printf("%lld\n", query(1, x, y));
            }
        }
        puts("");
    }
    return 0;
}

GSS 5

依旧是求最大子段和的问题，不过它强制左右端点在两个区间\(\{x_1, y_1\} \{x_2, y_2\}\)中。

我们考虑分类讨论：

  • 当\(y_1 < x_2\)时，即两个区间不重叠，那么最大子段和很显然就是\(\{x_1,y_1\}\)的最大后缀和\(+\{y_1,x_2\}\)的区间和\(+\{x_2,y_2\}\)的最大前缀和。

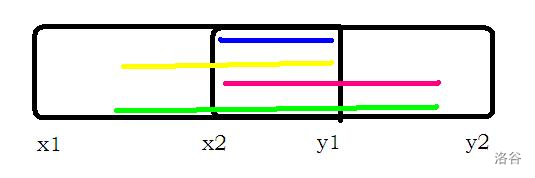
图片较简陋，凑合着看……

  • 当\(x_2 < y_1\)时，即两个区间有重叠部分，如同上图描述的情况，这时，我们需要考虑四种情况，区间\(\{y_1,x_2\}\)的区间和\((\)上图蓝色线段\()\)，区间\(\{x_1,y_1\}\)的最大后缀和\(+\{y_1,x_2\}\)的区间和\((\)上图黄色线段\()\)，区间\(\{y_1,x_2\}\)的区间和\(+\{x_2,y_2\}\)的最大前缀和\((\)上图粉色线段\()\)，区间\(\{x_1,y_1\}\)的最大后缀和\(+\{y_1,x_2\}\)的区间和\(+\{x_2,y_2\}\)的最大前缀和\((\)上图绿色线段\()\)。

此题还有两个需要注意的地方\(:\)

  • 当查询到\(l > r\)时要返回空节点，否则会像我一样\(RE\)到死\(……\)

  • 此题的最大子段和没有要求不能为空，所以我们在每次更新时都需要和\(0\)进行比较。

code:

#include <iostream>
#include <cstdio>
#include <cstring>
#include<bits/stdc++.h>

namespace LXC
{
    template<class T>
    inline T read(T &x)
    {
        x = 0; int w = 1, ch = getchar();
        while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
        while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}
        return x *= w;
    }

    template<class T>
    inline T max(const T a, const T b)
    {
        return a > b ? a : b;
    }
}
using namespace LXC;

const int maxn = 1e4 + 5;
int T, n, m, a[maxn];

struct Node {
    int l, r, sum, lsum, rsum, maxsum;
}z[maxn << 2], nmsl;

Node operator + (const Node &a, const Node &b)
{
    Node ans;
    ans.l = a.l;
    ans.r = b.r;
    ans.lsum = max(a.lsum, a.sum + b.lsum);
    ans.rsum = max(b.rsum, b.sum + a.rsum);
    ans.maxsum = max(max(a.maxsum, b.maxsum), a.rsum + b.lsum);
    ans.sum = a.sum + b.sum;
    return ans;
}

void build(int rt, int l, int r)
{
    z[rt].l = l, z[rt].r = r;
    if (l == r) {
        z[rt].sum = z[rt].lsum = z[rt].rsum = z[rt].maxsum = a[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

Node query(int rt, int l, int r)
{
    if (l > r) return nmsl;
    if (l == z[rt].l && z[rt].r == r) return z[rt];
    int mid = (z[rt].l + z[rt].r) >> 1;
    if (r <= mid)
        return query(rt << 1, l, r);
    if (l > mid)
        return query(rt << 1 | 1, l, r);
    return query(rt << 1, l, mid) + query(rt << 1 | 1, mid + 1, r);
}

int main()
{
    read(T);
    while (T--) {
        read(n);
        for (int i = 1; i <= n; i++) read(a[i]);
        build(1, 1, n);
        read(m);
        int x1, y1, x2, y2;
        for (int i = 1; i <= m; i++) {
            read(x1), read(y1), read(x2), read(y2);
            if (y1 < x2) {
                printf("%d\n", max(query(1, x1, y1 - 1).rsum, 0) + query(1, y1, x2).sum + max(query(1, x2 + 1, y2).lsum, 0));
            }
            else {
                int ans = query(1, x2, y1).maxsum;
                ans = max(ans, query(1, x1, x2 - 1).rsum + query(1, x2, y1).lsum);
                ans = max(ans, query(1, x2, y1).rsum + query(1, y1 + 1, y2).lsum);
                ans = max(ans, max(query(1, x1, x2 - 1).rsum, 0) + query(1, x2, y1).sum + max(0, query(1, y1 + 1, y2).lsum));
                printf("%d\n", ans);
            }
        }
    }
    return 0;
}

GSS 6

题目要求：插入元素，删除元素，单点修改，查询最大子段和。

很明显看到插入操作和删除操作，我们就知道这题要用平衡树，本人使用\(fhq~Treap\)来实现这些操作。

一些需要注意的点\(:\)

  • 在进行\(split\)时，我们习惯上采用按照权值来分，但这道题在哪个位置就把另设的一个权值标上位置，所以我们直接按照点的\(size\)来分。

  • 由于是平衡树，我们需要考虑左右子树是否为空的情况，所以我们采取常用的分类讨论的方式，唯一一点就是这样写下来你的\(update\)函数可能会巨长\(……\)

  • 本题我们用平衡树，因此在维护一个节点时，会分成左子树，自己，右子树三个部分，和线段树略有不同。

  • 这个题需要的空间很大，推荐直接开\(4\)倍。

  • 十年\(OI\)一场空，不开\(long~long\)见祖宗！！

code:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <ctime>
#define LL long long

namespace LXC
{
    template<class T>
    inline T read(T &x)
    {
        x = 0; int w = 1, ch = getchar();
        while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
        while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}
        return x *= w;
    }

    template<class T>
    inline T max(const T a, const T b)
    {
        return a > b ? a : b;
    }
}

using namespace LXC;

const int maxn = 4e5 + 5;
int n, m;
int l, r, _z, temp, opt;

struct Node {
    int ls, rs, size, key;
    LL val, sum, lsum, rsum, maxsum;
}z[maxn];
int root, cnt;

inline void update(int rt)
{
    z[rt].sum = z[rt].val, z[rt].size = 1;
    if (z[rt].ls)
        z[rt].sum += z[z[rt].ls].sum, z[rt].size += z[z[rt].ls].size;
    if (z[rt].rs)
        z[rt].sum += z[z[rt].rs].sum, z[rt].size += z[z[rt].rs].size;
    if (z[rt].ls && z[rt].rs) {
        z[rt].lsum = max(z[z[rt].ls].lsum, z[z[rt].ls].sum + z[rt].val + z[z[rt].rs].lsum);
        z[rt].rsum = max(z[z[rt].rs].rsum, z[z[rt].rs].sum + z[rt].val + z[z[rt].ls].rsum);
        z[rt].maxsum = max(z[z[rt].ls].maxsum, max(z[z[rt].rs].maxsum, z[z[rt].ls].rsum + z[z[rt].rs].lsum + z[rt].val));
    }
    else if (z[rt].ls) {
        z[rt].lsum = max(max(z[z[rt].ls].lsum, z[z[rt].ls].sum + z[rt].val), 0ll);
        z[rt].rsum = max(z[z[rt].ls].rsum + z[rt].val, 0ll);
        z[rt].maxsum = max(z[z[rt].ls].maxsum, z[z[rt].ls].rsum + z[rt].val);
    }
    else if (z[rt].rs) {
        z[rt].lsum = max(z[z[rt].rs].lsum + z[rt].val, 0ll);
        z[rt].rsum = max(max(z[z[rt].rs].rsum, z[z[rt].rs].sum + z[rt].val), 0ll);
        z[rt].maxsum = max(z[z[rt].rs].maxsum, z[z[rt].rs].lsum + z[rt].val);
    }
    else {
        z[rt].lsum = z[rt].rsum = max(z[rt].val, 0ll);
        z[rt].maxsum = z[rt].val;
    }
}

inline int insert(int x)
{
    ++cnt;
    z[cnt].size = 1;
    z[cnt].key = rand();
    z[cnt].val = z[cnt].sum = z[cnt].maxsum = x;
    z[cnt].lsum = z[cnt].rsum = max(x, 0);
    return cnt;
}

inline int merge(int x, int y)
{
    if (!x || !y) return x + y;
    if (z[x].key < z[y].key) {
        z[x].rs = merge(z[x].rs, y);
        update(x);
        return x;
    }
    else {
        z[y].ls = merge(x, z[y].ls);
        update(y);
        return y;
    }
}

inline void split(int rt, int x, int &l, int &r)
{
    if (!rt) {l = r = 0; return ;}
    if (x <= z[z[rt].ls].size) {
        r = rt, split(z[rt].ls, x, l, z[rt].ls);
    }
    else {
        l = rt, split(z[rt].rs, x - z[z[rt].ls].size - 1, z[rt].rs, r);
    }
    update(rt);
}

int main()
{
    char ch;
    srand((unsigned)time(NULL));
    read(n);
    for (int i = 1; i <= n; i++) {
        read(temp);
        split(root, i, l, r);
        root = merge(merge(l, insert(temp)), r);
    }
    read(m);
    for (int i = 1; i <= m; i++) {
        std::cin >> ch;
        if (ch == 'I') {
            read(opt), read(temp);
            split(root, opt - 1, l, r);
            root = merge(merge(l, insert(temp)), r);
        }
        else if (ch == 'D') {
            read(opt);
            split(root, opt, l, _z);
            split(l, opt - 1, l, r);
            r = merge(z[r].ls, z[r].rs);
            root = merge(merge(l, r), _z);
        }
        else if (ch == 'R') {
            read(opt), read(temp);
            split(root, opt, l, _z);
            split(l, opt - 1, l, r);
            z[r].val = temp;
            z[r].sum = z[r].maxsum = temp;
            z[r].lsum = z[r].rsum = max(temp, 0);
            root = merge(merge(l, r), _z);
        }
        else {
            read(opt), read(temp);
            split(root, temp, l, _z);
            split(l, opt - 1, l, r);
            printf("%lld\n", z[r].maxsum);
            root = merge(merge(l, r), _z);
        }
    }
    return 0;
}

GSS 7

\(GSS\)系列唯一一道树上的题目，虽然仅仅是将操作挪到了树上，但代码的难度确实是倍增\(……\)

考虑到我们的操作是在树上，所以我们首先用树链剖分将它映射到序列上，然后对序列进行操作。

本人觉得这道题的难点在于询问操作上，其他的操作都很常规。

关于询问操作\(:\)

  • 考虑到两个点都在向他们的\(LCA\)跳，我们分别记录两个答案\(L,R\)，最后返回答案时，再用重载后的加法将\(L\)和\(R\)合并起来。

  • 再我们进行最后一步合并前，我们需要交换一下\(L\)的最大前缀和和最大后缀和。不太明白？ 看图\(:\)

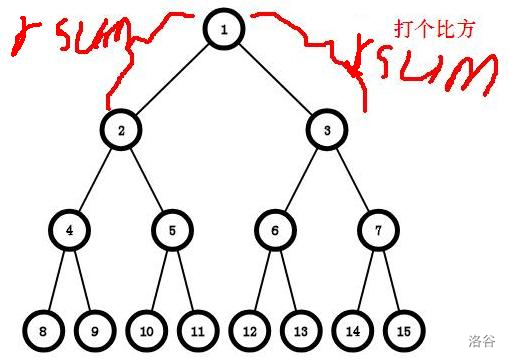
例如，我们要求\(9\)号节点到\(14\)号节点这条链上的最大子段和，当这两个点跳到他们的\(LCA\)即\(1\)号节点时进行合并操作，但我们发现，这时\(L\)的最大前缀和和\(R\)的最大后缀和连在了一起，如果这时合并，很明显是错的，所以我们需要将\(L\)的最大前缀和和最大后缀和交换一下。

然后，注意一下代码细节和常数问题就好了。

code:

#include <iostream>
#include <cstdio>
#include <cstring>

namespace LXC
{
    template<class T>
    inline T read(T &x)
    {
        x = 0;
        int w = 1, ch = getchar();
        while (ch < '0' || ch > '9') {if (ch == '-') w = -1; ch = getchar();}
        while (ch >= '0' && ch <= '9') {x = x * 10 + ch - 48; ch = getchar();}
        return x *= w;
    }

    template<class T>
    inline T max(const T a, const T b)
    {
        return a > b ? a :b;
    }
}

using namespace LXC;

const int maxn = 1e5 + 5;
int n, m, val[maxn], head[maxn], tot;
int dep[maxn], size[maxn], fa[maxn], son[maxn], top[maxn], idx[maxn], a[maxn], num, cnt;

struct Node {
    int sum, lsum, rsum, maxsum, tag;
    bool cov;
    Node(){sum = lsum = rsum = maxsum = 0;}
}z[maxn << 2];

struct Edge {
    int to, nxt;
}edge[maxn << 1];

void add(int from, int to)
{
    edge[++tot].to = to;
    edge[tot].nxt = head[from];
    head[from] = tot;
}

void dfs1(int u, int f, int deep)
{
    dep[u] = deep;
    fa[u] = f;
    size[u] = 1;
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == f) continue;
        dfs1(v, u, deep + 1);
        size[u] += size[v];
        if (size[v] > size[son[u]]) son[u] = v;
    }
}

void dfs2(int u, int topf)
{
    top[u] = topf;
    idx[u] = ++num;
    a[num] = val[u];
    if (!son[u]) return ;
    dfs2(son[u], topf);
    for (int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
}

Node operator + (const Node &a, const Node &b)
{
    Node ans;
    ans.sum = a.sum + b.sum;
    ans.lsum = max(a.lsum, a.sum + b.lsum);
    ans.rsum = max(b.rsum, a.rsum + b.sum);
    ans.maxsum = max(max(a.maxsum, b.maxsum), a.rsum + b.lsum);
    ans.tag = ans.cov = 0;
    return ans;
}

void build(int rt, int l, int r)
{
    if (l == r) {
        z[rt].sum = a[l];
        z[rt].lsum = z[rt].rsum = z[rt].maxsum = max(z[rt].sum, 0);
        z[rt].cov = 0;
        return ;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

void update(int rt, int l, int r, int k)
{
    z[rt].sum = (r - l + 1) * k;
    z[rt].lsum = z[rt].rsum = z[rt].maxsum = max(z[rt].sum, 0);
    z[rt].tag = k, z[rt].cov = 1;
}

void pushdown(int rt, int l, int r)
{
    if (!z[rt].cov) return ;
    int mid = (l + r) >> 1;
    update(rt << 1, l, mid, z[rt].tag);
    update(rt << 1 | 1, mid +1, r, z[rt].tag);
    z[rt].tag = z[rt].cov = 0;
}

void modify(int rt, int x, int y, int l, int r, int k)
{
    if (x <= l && r <= y) {
        update(rt, l, r, k);
        return ;
    }
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (x <= mid)
        modify(rt << 1, x, y, l, mid, k);
    if (y > mid)
        modify(rt << 1 | 1, x, y, mid + 1, r, k);
    z[rt] = z[rt << 1] + z[rt << 1 | 1];
}

Node query(int rt, int x, int y, int l, int r)
{
    Node L, R;
    if (x <= l && r <= y)
        return z[rt];
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (x <= mid)
        L = query(rt << 1, x, y, l, mid);
    if (mid < y)
        R = query(rt << 1 | 1, x, y, mid + 1, r);
    return L + R;
}

void uprange(int x, int y, int k)
{
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
        modify(1, idx[top[x]], idx[x], 1, n, k);
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) std::swap(x, y);
    modify(1, idx[x], idx[y], 1, n, k);
}

Node range(int x, int y)
{
    Node L, R;
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) {
            R = query(1, idx[top[y]], idx[y], 1, n) + R;
            y = fa[top[y]];
        }
        else {
            L = query(1, idx[top[x]], idx[x], 1, n) + L;
            x = fa[top[x]];
        }
    }
    if (dep[x] <= dep[y])
        R = query(1, idx[x], idx[y], 1, n) + R;
    else
        L = query(1, idx[y], idx[x], 1, n) + L;
    std::swap(L.lsum, L.rsum);
    return L + R;
}

int main()
{
    int x, y;
    read(n);
    for (int i = 1; i <= n; i++) read(val[i]);
    for (int i = 1; i <= n - 1; i++) {
        read(x), read(y);
        add(x, y), add(y, x);
    }
    dfs1(1, 0, 1);
    dfs2(1, 1);
    build(1, 1, n);
    read(m);
    int opt, u, v, w;
    while (m--) {
        read(opt);
        if (opt == 1) {
            read(u), read(v);
            Node ans = range(u, v);
            printf("%d\n", ans.maxsum);
        }
        else {
            read(u), read(v), read(w);
            uprange(u, v, w);
        }
    }
    return 0;
}

同样出自某钟姓神仙之口：“\(GSS\)系列本来只有\(7\)道题，第八道是后面人又加上的。”

再加上蒟蒻最近写数据结构有点恶心，预计将会在
天后将会更新\(GSS8.\)

咕咕咕\(……\)

猜你喜欢

转载自www.cnblogs.com/Hydrogen-Helium/p/11737195.html
今日推荐
基于大语言模型的开源知识库问答系统 MaxKB GitHub Star 数量突破 5,000 个！
美国拟限制 AI 大模型出口中国和俄罗斯
苹果将与 OpenAI 达成协议，将 ChatGPT 应用于 iPhone
openKylin 社区生态委员会第六次会议圆满召开
阿里云正式发布通义千问 2.5
Python 3.13 发布首个 Beta：实验性自由线程模式和 JIT、改进交互式解释器
Stack Overflow 拿我的代码去训练 AI 大模型，还封了我的账号
Pop!_OS 的 COSMIC 桌面完成 App Store 上架工作
《2024 年一季度互联网投融资运行情况》研究报告
报告：Django 仍然是 74% 开发者的首选
15 年前上了“FFmpeg 耻辱柱”，今天他还得谢谢咱——腾讯QQPlayer一雪前耻？
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
周排行
记一下去大梅沙的准备（2018-05-26）
Spring 注解 事务
基于HTTP协议的客户端缓存
阿里云rds 备份和还原
[PHP] 几个拖慢 PHP 程序/API 运行速度的点
python 代码风格------------PEP8规则
js控制json生成菜单——自制菜单（一）
将字符串: 'k:1|k1:2|k2:3|k3:4 ' ,处理成 python 字典: {'k':1, 'k1':2, ...}
微信小程序转支付宝小程序
Qt551.窗口滚动条
每日归档
更多
2024-05-13(18)
2024-05-12(0)
2024-05-11(38)
2024-05-10(38)
2024-05-09(35)
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022