数据结构之堆与Java实现

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/qq_45608306/article/details/102641522

一、堆

1.堆的概念

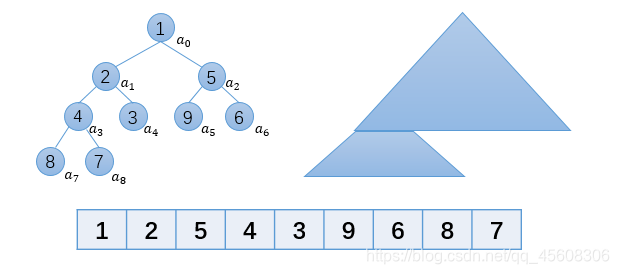
堆时一个数组，它可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素 。除了树的最底层外，该树是完全充满的，底层不满时从左往右填充。

2.堆的性质

2.1 堆的高度
把堆看作一颗树，则堆中某个结点的高度就是该结点到叶结点最长简单路径上的边的数目。如此一来，堆的高度就是堆顶到叶子节点的最长简单路径上的边的数量。也即 $lg(N)$,之后我们可以发现，堆结构上的一些基本操作运行时间均与堆的高度成正比。

2.2 堆结点的位置关系
观察1中的图可以很容易得出结论,父结点与左右子结点的下标有如下关系：
$parent(i) = \lfloor (i-1)_/2 \rfloor$
$leftchild(i) = 2i+1$
$rightchild(i) = 2i+2$

2.3 堆结点的大小关系
二叉堆分为两种形式：大根堆和小根堆。故名思意可以想到，大根堆就是最大的元素在堆顶，小根堆就是最小的元素在堆顶。除此之外，堆的父结点与子结点维持严格的大小关系。
大根堆：
$a[0] = max(a)$
$a[parent(i)] \geq a[i]$
小根堆：
$a[0] = min(a)$
$a[parent(i)] \leq a[i]$

二、堆的实现(以大根堆为例)

1.基本成员

    private static final int defaultsize = 10;  //默认大小
    private final Comparator<? super E> comparator;  //比较器
    private Object[] heaplist;   //数组
    private int size = 0;     //堆大小

2.向下调整堆

假定a[i]的子树,即以 $a[leftchild(i)]和a[rightchild(i)]$为根的树均符合大根堆的性质。而 $a[i]<a[[leftchild(i)]或a[i]<a[rightchild(i)]$，这样就违背了大根堆的性质。此时，可以通过让 $a[i]$的值在堆中"逐级下降"，使得以 $a[i]$为根的树符合大根堆的特性。
如图：

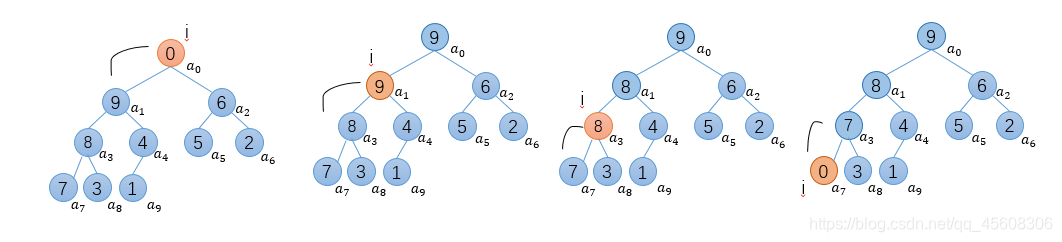
代码如下：

    private void siftDown(E X, int i){ //参数为需要调整的对象及其索引
    int half = size >>> 1;
    while (i< half){    //直到到没有子结点
        int leftChildIndex = (i << 1) + 1;  //左子结点索引
        int rightChildIndex = leftChildIndex+1;   //右子结点索引
        Object temp = heaplist[leftChildIndex];   //选取左子结点作为临时值
        if(rightChildIndex<size&&comparator.compare((E)temp,(E)heaplist[rightChildIndex])<0){
        	//比较，选取较大那个作为临时值
            temp = heaplist[leftChildIndex=rightChildIndex];
        }
        if (comparator.compare((E)X,(E)temp)>=0)
        	//与临时值，也即左右子结点最大的比较，如果比它们都大，说明符合大根堆性质，退出循环
            break;
        heaplist[i] = temp;   //替换为临时值
        i = leftChildIndex;  //修改索引，进行下一层的检测
    }
    heaplist[i] = X; 
}

3.建堆

由于 $a[size/2]到a[size-1]$是没有子结点的，因此，它们都符合堆的性质，因而不需要调整它们。之后从 $size/2-1$处直到根节点都进行"向下调整堆"的操作即可完成建堆。
从后往前，i是持续减小的：

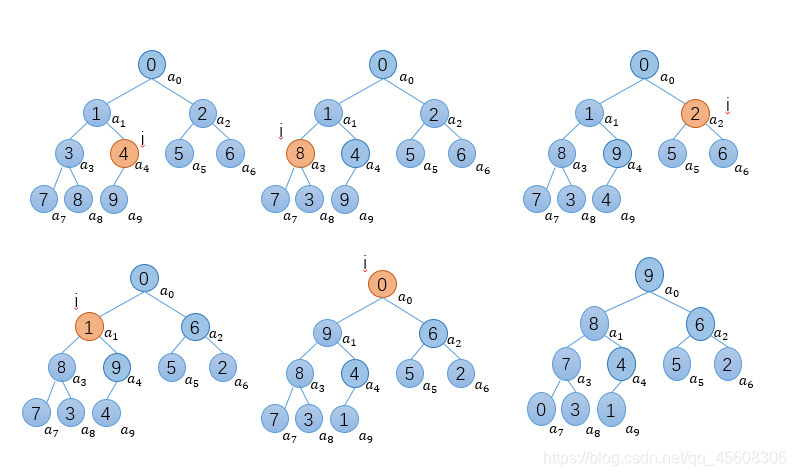
代码如下：

    private void buildHeap(Object[] inputlist,Comparator<? super E> comparator){
        for (int i= (size>>>1) - 1; i>=0; i--){
            siftDown((E) heaplist[i], i);
        }
    }

为何从后面开始调整而不是前面呢？
因为后面开始，结点的子树都能保证是符合堆的性质的，将其"向下调整"之后，包括该结点本身也符合堆的性质。这样，到该结点的父结点”向下调整堆“时，也可保证子结点是符合堆性质从而调用该方法不会产生问题。

4.向上调整堆

将堆用于优先级队列时，需要对入队元素进行向上调整，使得其符合堆的性质；又或者，在堆排序时，新加入一个元素，此时不需要重新建堆，而只需要向上调整堆即可保持堆的结构。
向上调整堆要比向下调整堆来得简单，只需要一直对根节点进行比较然后替换即可。

    public void siftUp(E X,int i){
        while (i > 0){
            int parentIndex = (i - 1) >>> 1;   //父结点索引
            Object temp = heaplist[parentIndex];  //取父结点值
            if (comparator.compare(X,(E)temp)<=0)  //比父结点小，结束调整
                break;
            heaplist[i] = temp;   //父结点值(更小)作为该位置值
            i = parentIndex;        //更新索引，继续与上面比较
        }
        heaplist[i] = X;
    }

5.插入元素与删除元素

插入元素只需要将元素放在数组，再对它调用"向上调整堆"方法即可。
删除元素只需要使用最后一个元素取代堆顶元素，然后对其调用"向下调整堆"方法即可。
插入元素的应用：
优先级队列中的入队；进行自顶向下的建堆…
删除元素的应用：
优先级队列中的出队；堆排序中，抛出已排序好的元素…

6.全代码

public class MyHeap<E>{
    private static final int defaultsize = 10;
    private final Comparator<? super E> comparator;
    private Object[] heaplist;
    private int size;

    public MyHeap(Object[] inputArray, Comparator<? super E> comparator){
        heaplist = inputArray;
        this.size = inputArray.length;
        this.comparator = comparator;
        buildHeap(comparator);
    }

    public MyHeap(Object[] inputArray, int size, Comparator<? super E> comparator) throws Exception{
        if (inputArray.length>size){
            throw new Exception("out of size");
        }
        heaplist = new Object[size];
        for (int i = 0;i<inputArray.length;i++){
            heaplist[i] = inputArray[i];
        }
        this.size = inputArray.length;
        this.comparator = comparator;
        buildHeap(comparator);
    }

    @SuppressWarnings("unchecked")
    private void buildHeap(Comparator<? super E> comparator){
        for (int i= (size>>>1) - 1; i>=0; i--){
            siftDown((E)heaplist[i], i);
        }
    }

    @SuppressWarnings("unchecked")
    private void siftDown(E X, int i){
        int half = size >>> 1;
        while (i< half){
            int leftChildIndex = (i << 1) + 1;
            int rightChildIndex = leftChildIndex+1;
            Object temp = heaplist[leftChildIndex];
            if(rightChildIndex<size&&comparator.compare((E)temp,(E)heaplist[rightChildIndex])<0){
                temp = heaplist[leftChildIndex=rightChildIndex];
            }
            if (comparator.compare(X,(E)temp)>=0)
                break;
            heaplist[i] = temp;
            i = leftChildIndex;
        }
        heaplist[i] = X;
    }

    @SuppressWarnings("unchecked")
    public void siftUp(E X,int i){
        while (i > 0){
            int parentIndex = (i - 1) >>> 1;
            Object temp = heaplist[parentIndex];
            if (comparator.compare(X,(E)temp)<=0)
                break;
            heaplist[i] = temp;
            i = parentIndex;
        }
        heaplist[i] = X;
    }

    public void insert(E X) throws Exception{
        if (size==heaplist.length){
            throw new Exception("out of size");
        }
        heaplist[size] = X;
        siftUp(X,size);
        size++;
    }
	
	 public Object extract() throws Exception{
	    if (size == 0){
	        throw new Exception("empty");
	    }
	    Object obj = heaplist[0];
	    size--;
	    heaplist[0] = heaplist[size];
	    siftDown((E)heaplist[0],0);
	    return obj;
	}
    
    public void printHeap(){
        for (int i=0;i<size;i++){
            System.out.println(heaplist[i]);
        }
    }
}

7.测试代码及结果

public class Main {
    public static void main(String[] args) throws Exception{
        Integer a[]  = new Integer[10];
        for (int i =0;i< 10;i++)
            a[i] = i;
        MyHeap h = new MyHeap(a,12, new MyComparator());
        h.printHeap();
        System.out.println(h.extract());
        h.printHeap();
        h.insert(10);
        h.printHeap();
        h.insert(100);
        h.printHeap();
    }
}

class MyComparator implements Comparator<Integer>{
    @Override
    public int compare(Integer a, Integer b) {
        return a - b;
    }
}

结果：
9 8 6 7 4 5 2 0 3 1
9
8 7 6 3 4 5 2 0 1
10 8 6 3 7 5 2 0 1 4
100 10 6 3 8 5 2 0 1 4 7

三、性能分析

1.向下调整堆

对父亲结点与子结点进行比较替换的操作时间复杂度为常数，而在树的最低层是半满的情况时，发生最坏的情况：
$T(N)\leq T(2N/3) + \Theta(1)$
     $\leq T(\frac{2^2N}{3^2})+\Theta(2)$
     $\cdots\cdots$
     $\leq T(\frac{2^kN}{3^k})+\Theta(k)$
     $\leq T(1)+\Theta(lg_\frac{3}{2}N)$
故向下调整堆的时间复杂度为 $O(lgN)$

2.向上调整堆

类似向下调整堆可知上调堆的时间复杂度为 $O(lgN)$

3.建堆

自底向上建堆，由于需要向下调整的结点个数为 $\frac{N}{2}$，因此通过向下调整堆地时间复杂度 $O(lgN)$可推断建堆的一个时间复杂度上界为 $O(NlgN)$
这样考虑，先建左子树堆和右子树堆，之后"向下调整堆"来完成建堆，故有：
$T(N)= 2T(N/2) + O(lgN)$
     $= 4T(N/2^2)+O(lgN)+O(lg\frac{N}{2})$
     $\cdots\cdots$
     $= NT(1)+ O(lgN)+O(lg\frac{N}{2})+\cdots+O(1)$
故其时间复杂度为 $O(N)$

或可对一个满二叉树作如下分析：
易知一个完全二叉树高度为 $\lfloor lgN \rfloor+1$，设 $h=\lfloor lgN \rfloor$
根结点为1，调整根结点次数为 $h$；第二层结点数量为2，调整 $h-1$次，依次类推得，(h-1)层需要调整一次。
故 $S=2^0\cdot h+2^1\cdot(h-1)+\cdots+2^{h-1}\cdot1$
$2S=2^1\cdot h+2^2\cdot(h-1)+\cdots+2^{h}\cdot1$
$S=2S-S$
   $=-2^0\cdot h+2^1+2^2+\cdots+2^{h-1}+2^{h}$
   $=3\cdot2^h-h-2$
   $=3N-lgN-2$
故其时间复杂度为 $O(N)$

4.插入元素与删除元素

它们的时间复杂度分别为”向上调整堆“和”向下 调整堆“再附加一个常数时间的操作，因此时间复杂度也为 $O(lgN)$

四、斐波那契堆

斐波那契堆的删除操作和合并操作具有比二叉堆更优秀的时间渐进界，其他情况时间渐进界与二叉堆相同。值得注意的时斐波那契堆的合并操作可以在常数时间内完成，比二叉堆的最坏情况下的线性时间复杂度要好得多。

待填。。。