若平面向量\(\left| \boldsymbol{a}\right|=2\),\(\left| \boldsymbol{b}\right|=3\),\(\left| \boldsymbol{e}\right|=1\),且\(\boldsymbol{a}\cdot\boldsymbol{b}-\boldsymbol{e}\cdot\left(\boldsymbol{a}+\boldsymbol{b}\right)+1=0\).则\(\left| \boldsymbol{a}-\boldsymbol{b}\right|\)的最小值是\((\qquad)\)
\(\mathrm{A}.1\) \(\qquad\mathrm{B}.2\sqrt{3}-1\) \(\qquad\mathrm{C}.\sqrt{12-4\sqrt{3}}\) \(\qquad\mathrm{D}.\sqrt{7}\)
解析: 法一 矩形的性质 由题设\[(\boldsymbol{a},\boldsymbol{b},\boldsymbol{e})=\left( \overrightarrow{OA} , \overrightarrow{OB} , \overrightarrow{OE} \right)\]如图所示,
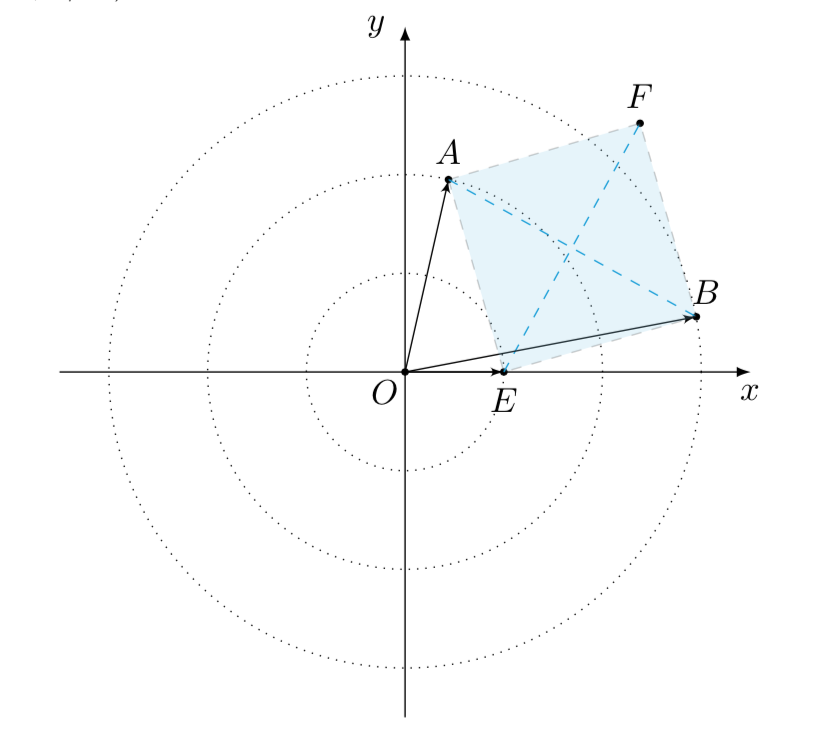
易知 \(EA\perp EB\),构造矩形 \(FAEB\),不妨固定 \(E\)点,则由矩形性质可知 \[ |OF|^2+|OE|^2=|OA|^2+|OB|^2.\]所以 \(F\)点的轨迹方程为 \[x^2+y^2=12.\]从而 \(|\boldsymbol{a}-\boldsymbol{b}|\),即 \(|AB|\),也即 \(|EF|\)的最小值为 \(2\sqrt{3}-1\).
法二 由题\[ |\boldsymbol{a}\cdot \boldsymbol{b}+1|=|\boldsymbol{e}\cdot\left(\boldsymbol{a}+\boldsymbol{b}\right)|\leqslant |\boldsymbol{a}+\boldsymbol{b}|.\]两边平方可得\[ \left(\boldsymbol{a}\cdot\boldsymbol{b}\right)^2+2\cdot\boldsymbol{a}\cdot\boldsymbol{b}+1\leqslant \boldsymbol{a}^2+\boldsymbol{b}^2+2\cdot \boldsymbol{a}\cdot\boldsymbol{b}. \]所以\[-2\sqrt3\leqslant \boldsymbol{a}\cdot \boldsymbol{b}\leqslant 2\sqrt{3}.\]因此\[ |\boldsymbol{a}-\boldsymbol{b}|=\sqrt{\boldsymbol{a}^2+\boldsymbol{b}^2-2\cdot \boldsymbol{a}\cdot \boldsymbol{b}}\geqslant \sqrt{13-4\sqrt{3}}=2\sqrt{3}-1.\]
当\(\boldsymbol{e}\)与\(\boldsymbol{a}+\boldsymbol{b}\)同向时取等.因此所求表达式的最小值为\(2\sqrt{3}-1\).