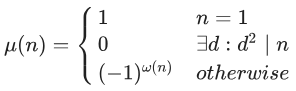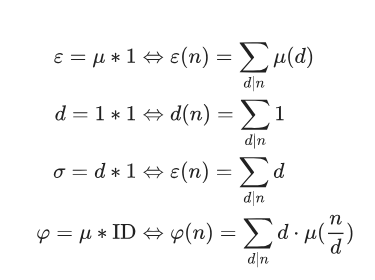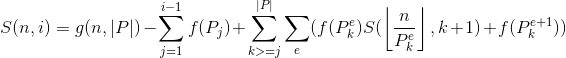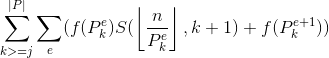【数论专题】——推式子（2019/8/21更新）

今天主要就是推式子。

数论函数专题。

本文会参考大量资料（或者说照搬），会注明资料来源。

https://oi-wiki.org/(定义和证明等)

前置知识：

积性函数：形如 $f(x)f(y)=f(xy)\ (x\perp y)$ ,则称 $f(x)$ 为积性函数。

几个必备积性函数：

欧拉函数:

　　 $\phi(n)=\sum^n_{i=1}[(i,n)=1]$

莫比乌斯函数：

　

扫描二维码关注公众号，回复： 7070978 查看本文章

恒等函数：

　 $id_k(n)=n^k$ ,其中 $id_1(n)=n$ 通常记为 $id(n)$

单位函数：

　 $\varepsilon (n)=[n=1]$

除数函数：

　 $\sigma_k(n)=\sum_{d \mid n}d^k$

　 $\sigma_0(n)$ 通常记做d(n)。

常数函数：

　 $1(n)=1$

几个结论：

　　　　 $n=\prod_{i=1}^{p_0}{p_i}^{c_i}$

　　　　　 $\phi(n)=(\prod[q_i\leq 1])*(-1)^{p_0}$

　　　　　(推导使用)：

　　　　 $\sum_{d\mid n}\mu(d)=[n=1]$

　　　　 $\sum_{d\mid n}\phi(d)=n$

Dirichlet卷积：对于两个数论函数f,g,两者的Dirichlet卷积为：

$(f*g)(n)=\sum_{d\mid n}f(d)g(\frac{n}{d})$

一些基本的卷积式子：

（图源OIwiki）

这些式子对化简题目有极大作用。

　　既然是推式子，直接从一道例题入手：

　　求：

　　 $\sum_{i=1}^{n}\sum_{j=1}^{n}(i,j)$

　　如果考虑朴素做法，对于n太大的情况无从下手，那么我们来简化式子。

　　我们考虑引入莫比乌斯函数：

　　我们枚举(i,j)的大小：

　　 $\Rightarrow \sum_{d=1}^{n}\sum_{i=1}^{n}\sum_{j=1}^{n}[(i,j)=d]*d$

　　式子内同除以d，得到：

　　 $\Rightarrow \sum_{d=1}^{n}\sum_{i=1}^{\left \lfloor \frac{n}{d}\right \rfloor}\sum_{j=1}^{\left \lfloor \frac{n}{d}\right \rfloor}[(i,j)=1]*d$

　　引入莫比乌斯函数：

　 $\Rightarrow \sum_{d=1}^{n}\sum_{i=1}^{\left \lfloor \frac{n}{d}\right \rfloor}\sum_{j=1}^{\left \lfloor \frac{n}{d}\right \rfloor}\sum_{x\mid i \wedge x \mid j}\mu(x)*d$

　　将枚举顺序变换，同第一步，先枚举(i,j)，就可以把第四个sigma放到前面：

　 $\Rightarrow \sum_{d=1}^{n}*d*\sum_{x=1}^{\left \lfloor \frac{n}{d}\right \rfloor} \mu(x)\sum_{i=1}^{\left \lfloor \frac{n}{dx}\right \rfloor}\sum_{j=1}^{\left \lfloor \frac{n}{dx}\right \rfloor}$

　后面两个求和因为贡献是1，因此直接写成平方形式：

　 $\Rightarrow \sum_{d=1}^{n}*d*\sum_{x=1}^{\left \lfloor \frac{n}{d}\right \rfloor} \mu(x)\left \lfloor \frac{n}{xd} \right \rfloor^2$

这里其实就可以直接数论分块写了，但还可以继续推：

　　令 $T=dx$ ,枚举T的大小，并用Dirichlet卷积搞一搞：

　　 $\Rightarrow \sum_{T=1}^{n}\left \lfloor \frac{n}{T} \right \rfloor^2\sum_{d \mid T} \mu(\frac{T}{d})*d$

　　 $\Rightarrow \sum_{T=1}^{n}\left \lfloor \frac{n}{T} \right \rfloor^2*\phi(T)$

　　我们把phi用线性筛整出来，很容易就得到答案了。

来一道练手题：

P3327 [SDOI2015]约数个数和

最后用数论分块等东西搞搞就行了。

补充一个筛mu函数的模板：

 1 int vis[N],prime[N],mu[N],cnt;
 2 void mu_sieve(){
 3     mu[1]=1;
 4     for(int i=2;i<=N;i++){
 5         if(!vis[i]){
 6             prime[++cnt]=i;
 7             mu[i]=-1;
 8         }
 9         for(int j=1;j<=cnt;j++){
10             if(i*prime[j]>N) break;
11             vis[i*prime[j]]=1;
12             if(i%prime[j]==0){
13                 mu[i*prime[j]]=0;
14                 break;
15             }
16             else mu[i*prime[j]]=-mu[i];
17         }
18     }
19 }

在本题中，还需要筛出1~n的每个数约数个数和，可以看一下这位大佬的博客：GO

在线性筛基础上改造即可。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=5e4+10;
 4 int t,n,m;
 5 int vis[N],prime[N],mu[N],d[N],num[N],cnt;
 6 //vis 标记 prime 素数 mu 莫比乌斯函数 d 约数个数 num 最小质因子个数 
 7 void sieve(){
 8     vis[1]=d[1]=mu[1]=1;
 9     for(int i=2;i<=N;i++){
10         if(!vis[i]){
11             prime[++cnt]=i;
12             num[i]=1;
13             d[i]=2;
14             mu[i]=-1;
15         }
16         for(int j=1;j<=cnt&&i*prime[j]<=N;j++){
17             vis[i*prime[j]]=1;
18             if(i%prime[j]==0){
19                 mu[i*prime[j]]=0;
20                 d[i*prime[j]]=d[i]/(num[i]+1)*(num[i]+2);
21                 num[i*prime[j]]=num[i]+1;
22                 break;
23             }
24             else{
25                 d[i*prime[j]]=d[i]*d[prime[j]];
26                 num[i*prime[j]]=1;
27                 mu[i*prime[j]]=-mu[i];
28             } 
29         }
30     }
31     for(int i=1;i<=N;i++){
32         mu[i]+=mu[i-1];
33         d[i]+=d[i-1];
34     }
35     
36 }
37 int main(){
38     sieve();
39     scanf("%d",&t);
40     for(int k=1;k<=t;k++){
41         scanf("%d%d",&n,&m);
42         if(n>m) swap(n,m);
43         long long ans=0;
44         int i=1,j;
45         while(i<=n){
46             j=min(n/(n/i),m/(m/i));
47             ans+=1ll*(mu[j]-mu[i-1])*d[n/i]*d[m/i];
48             i=j+1;
49         }
50         printf("%lld\n",ans);
51     }
52     return 0;
53 }

（于8/21日更新）

筛。

抽空学了一下min_25筛，重新整理一下思路：

使用对象:

　　对于一个函数,需要满足以下三点：

是一个积性函数。

可以用一个较简单的多项式来表达

可以由快速求得

用途：求出包含以上三个要点的函数的前缀和。

质数部分：

　　　　先给个式子：

　　　　

表示小于等于n的所有数x中，最小质因子大于Pi或x本身为质数的函数和。

注意：这个函数把部分合数也当做质数处理了，但是本身不会影响答案统计，所以也是作者的明见之处。

对于这个过程：

我们去掉了Pi这个质因子，那么考虑两种情况：

对于一个最小质因子Pi，它能表达的最小合数就是Pi的平方，如果，则说明n中无Pi这个质因子，因此对答案没有贡献，可以直接转移。

如果包含这个最小质因子，那么就要减去所有含有质因子Pi的合数，即，但是这样又会重复减掉含有比Pi更小的质数的一些形如的数，因此还要加回来，即，组合起来就是上面那串式子了！

合数部分：

　　　　再来个式子：

　　　　

表示小于等于n的所有x中，最小质因子大于等于Pi的函数和。

（一个提醒：在质数部分中我们已经求出了的取值）

这个转移看起来好复杂，实际上也很简单：

对于前半部分：

　　分别是小于等于n的质数贡献之和，与不满足条件的部分,(质因子小于i的部分),合起来就是所有满足条件的质数贡献之和。

对于后半部分：

　　

　　第一个sigma是枚举质因数，第二个是枚举指数，实际上整个过程就是在处理合数的情况，最后那个小部分是用来处理形如的数，他们虽然也是合数，但因子只有一个并且是质数。

　　到这min_25筛的部分就基本结束了。什么？你问我板子怎么打？我也不知道。

　下一次会是什么呢？continue……

【数论专题】——推式子（2019/8/21更新）

质数部分：

合数部分：

猜你喜欢