本文的原始素材来源于:https://www.sohu.com/a/218689757_119719 美国顶级学术期刊宣布禁用p值,原来p值很危险
若想查看本文的ppt版本,请转至:https://mp.weixin.qq.com/s/pha2_VQVJ2vqshp6so7MgA
以下正文:
一、背景介绍
1月22日,美国政治学顶级学术期刊《政治分析》在他们的官方twitter上宣布从2018年的开始的第26辑起禁用p值。

根据该刊的声明,其主要原因是:p值本身无法提供支持相关模式或假说之证据
美国统计协会(ASA)在一篇关于p值的声明中也提到了6个准则:
P-values can indicate how incompatible the data are with a specified statistical model.
准则1:P值可以表达的是数据与一个特定统计模型不匹配的程度。P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
准则2:P值并不能衡量研究假设为真的概率,也不能衡量数据仅由随机因素产生的概率。Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
准则3:科学结论、商业或政策决策不应该只建立在p值是否通过特定临界值的基础上。Proper inference requires full reporting and transparency
准则4:合理的推断过程需要数据报告的完整性和透明性。A p-value, or statistical significance, does not measure the size of an effect or the importance of a result.
准则5:P值或统计显著性并不能表明结果的重要性或影响程度大小。By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.
准则6:就p值本身而言,它不能提供良好的证据度量来支持模型或假设
先来看一下p值的使用现状:
通常研究者为了挤出显著的结果,只有在研究结果显著时才报告;研究结果不显著时,通通没有报告。这是一种只看到有利于结论的证据,忽略了不利证据的做法。这就是我们所说的摘樱桃现象(cherry-picking),因为只采摘成熟的、质量好的樱桃,而糟糕的樱桃你没有看见,并不代表它不存在,只是没有被公布出来而已。
举个例子来说明p值到底存在什么问题:
假设存在20个研究,每个研究的虚无假设都是正确的,那么单独的研究结果应该是不显著的;
当我们做了20个统计检验时,至少有一个结果显著的概率其实很高:
![]()
也就是说,即使我们把犯Ⅰ类错误的概率α控制在了0.05,至少有一次显著的概率依然可以高达64%!当你做了很多很多的实验,总会让你碰上一个显著的,然后你就兴高采烈地把这个“恰好”显著的结果报告出来了,但这只是你碰运气碰来的,实际是不显著的啊!
所以ASA在声明中给出的建议是:
实验者必须要 full reporting and transparency,不能有所遮掩,不能只报喜,不报忧;无论显著与否,都要把所有的实验结果报告出来!
二、p值是什么
p值的定义
p值是由 Ronald Fisher 在 1920 年代发展出来的,已将近一百年。《剑桥统计词典》中对P值的定义是:
P-value: The probability of the observed data (or data showing a more extreme departure from the null hypothesis) when the null hypothesis is true.(p 值:p值是零假设为真时,观察到目前的数据或者更偏离零假设数据的概率。)
p值检验
p值检验:检验在一个假定的model下,实验出来的data跟model是否吻合
这个假定的model,就是虚无假设(null hypothesis),一般是假设实验并无系统性效应的,即效应是零,或是随机状态,所以也叫零假设。例如:假设一个效应不存在,两组之间没有差异,因素与结局值之间没有相关性
在虚无假设之下,得到一个统计值,然后计算获得这么大(或这么小)的统计值的机率有多少,这个机率就是 p 值。
得到p值之后要做统计检定,我们约定俗成地设定一个显著性水平α,通常α=0.1,0.05,0.01。若p<α,则拒绝虚无假设,并宣称这个检定在统计上是显著的;否则检定不显著。


为什么p值很小,就拒绝虚无假设?
这里依据的是命题逻辑中,以否定后件来否定前件的方法(拉丁文称为modus tollens),即:
若P,则Q → 非Q,则非P
也就是说,如果P成立,可以推出Q成立;现在如果Q不成立,则反过来推出P也不成立。
而p值检定是一种有或然性的modus tollens,是probabilistic modus tollens:
若H0为真,则p值显著的概率很小,只有0.05 → p显著了,则否定H0
所谓或然性,就是不是绝对的,而是存在一定概率的。我们在p值检定中容许了这样一个概率的存在,即使这个概率很小很小
但是对于modus tollens来说,不应该有任何误差的余地,即如果原假设H0成立,则p值不可能显著,显著的概率应该为0;所以如果p值显著了,则推出原假设不成立。
也就是说,我们用命题逻辑来作统计推论,而推论方法跟命题逻辑却不完全一样?
到这里我们就可以提出疑问了,我们到底能不能够因为 p 值很小,小到可能性很低,就用否定后件的方法来否定前件?
p值的问题在于:如果容许或然性,这样的推论方法还可靠吗?
这里举两个例子用来感受一下为什么用p值来做统计推论有可能是错误的:
例1
若大乐透的开奖机制是完全随机的,则每注中头奖的机率很小,只有 1 / 13,980,000;
现在你中奖了,几乎不可能发生的事件发生了,所以大乐透开奖的机制不是随机的。
例2
基督教如何论证上帝创造了世界?
若上帝是不存在的,事情的发生都是by chance的,要随机生成像人体这么复杂的系统,几率很低很低,几乎不可能;
现在人是存在的,几乎不可能发生的复杂系统却发生了,所以上帝是存在的,人是by design的。
是不是觉得怪怪的呢?根据这种逻辑得出来的推论,我们似乎要打上一个问号了。
到这里,我们突然对老师每组随机抽人讲作业的机制提出疑问:若我们的小组作业不是大家一起做的,那么随机抽一个人,这个人会讲的概率应该很小;结果现在真的抽到一个会讲的人,所以得出我们的小组作业是大家一起做的,这个结论真的靠谱吗?(手动奸笑)
三、p值不是什么
假设检验中的两类错误
用下图的表来呈现有关虚无假设是对或者不对,是被拒绝或者被接受的四种可能性,其中两种是作出错误统计推论的情况。

第一个情况,虚无假设是对的,但统计检定是显著的,因此虚无假设被推翻了。这种情况叫做 Type I error,又叫拒真错误,用α表示,表示在H0为真的情况下,H0被拒绝的概率,通常我们保留了 0.05 的机率容许它存在。
α = Pr(Type Ⅰ Error) = Pr(H0 Rejected | H0 True)
第二个情况,如果虚无假设是错误的,但统计检定不显著,所以它没有被推翻,这个情况叫做 Type II error,又叫受伪错误,用β表示,表示H0为假的情况下,H0被接受的概率。
β = Pr(Type Ⅱ Error) = Pr(H0 Not Rejected | H0 False)
为了让大家更好地理解这个表格,我用另一种形式呈现出来(在机器学习里称为混淆矩阵),其中N为阴性,表示H0为真,P为阳性,表示H0为假(通常把我们需要关注的状态设为阳性,例如医院的检查报告,检测出存在某种疾病则显示阳性):

同样的表格,用abcd表示每种情况出现的案例数(而不是概率),此时:
α = a / (a + c)
β = d / (b + d)
此时我们给α和β另外一个名字,请大家务必要记住:
伪阳性率(α):实际为阴性,却被预测为阳性的概率
伪阴性率(β):实际为阳性,却被预测为阴性的概率
伪阳性的几率 vs 伪阳性的反几率
在p值检定里,p值告诉我们的是,如果虚无假设为真(N),我们"观察到数据"的概率有多少,也就是data的概率,即:
伪阳性的几率 = Pr(Test= + | H0)= a / (a + c) = α

但是!p值没有告诉我们,"虚无假设为真"的几率有多少,或"研究假设是对的"的几率有多少。也就是说,研究者最想知道的问题其实是,我观察到的数据出现时,H0正确的概率是多少(N),也就是model的概率,即:
伪阳性的反几率 = Pr(H0 | Test= +)= a / (a + b)

换言之,如果虚无假设为真,那么p值检定是显著的机率是 α = 0.05。但这其实不是我们作研究最想回答的问题;这个机率只告诉我们,如果你的虚无假设为真,有百分之五的机率,data 会跟它不合,但它没有告诉我们虚无假设这个 model 本身为真的机率有多少,而这才是我们应该问的问题。
原则上来说,伪阳性的几率和伪阳性的反几率不会相等,只有在a=0的时候,两者都是0才会相等。而前面我们说了,因为或然性的存在,a绝对不可能等于0,不然就不是统计了。
而且需要注意的是,伪阳性的反几率通常会很高,即使我们把α控制得很小很小。
贝叶斯定理计算反几率——铜板实验
举个例子来说明要如何计算反几率:
假设口袋里面有三个铜板,其中两个是正常铜板,即正面/反面的概率均为1/2;剩下一个是有偏差的铜板,正面概率1/3,反面概率2/3。
如果现在随机从口袋里掏出一个铜板,这个铜板是偏差铜板的概率是多少?
很简单,大家不要想太多,就是1/3 嘛!
P(偏差铜板) = 1/3
现在掏出这个铜板之后丢了一下,得到正面,这时候再问这个铜板是偏差铜板的概率是多少?
嗯,这个时候就要用到我们传说中的——贝叶斯公式了:
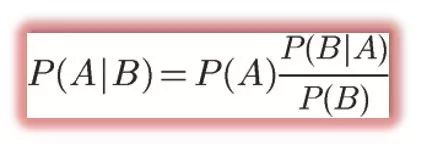
其中P(A)为先验概率(prior probability),P(A|B)为后验概率(posterior probability),表示在B发生的情况下A发生的概率 。
继续刚刚的铜板问题,现在要计算的是抛出正面(B)的情况下,这个铜板是偏差铜板(A)的概率,代入贝叶斯公式:
P( 偏差铜板 | 正面)
= P(偏差铜板) × P (正面 | 偏差铜板) / P (正面)
= (1/3 ) × (1/3 ) / [(2/3) × (1/2) + (1/3) × (1/3)]
= 1 / 4
因为偏差铜板出现正面的机率,比正常铜板要小,所以出现正面的话,它相对来讲就比较不太可能是偏差的铜板,所以机率会比原来的 1/3 小些,只有 1/4。
这时候大家要建立一个概念,在还没观察到数据之前,对于模型的机率的一些估计,叫做先验概率,例如这里的 P(偏差铜板) =1/3;当观察到数据之后所更新的模型几率,例如这里的 P( 偏差铜板 | 正面) =1/4,是后验概率,也就是我们前面说的——反机率(inverse probability) 。
贝叶斯定理计算反机率——药检实验
再来看另外一个跟统计检定问题非常接近的例子:
假设有数据表明大约有6%的美国 MLB 的球员使用 PED(一种增加体能表现的药物),这个 6 % 即为前面说的先验机率:随机选出一个球员,则他有使用 PED 的机率是 0.06,没有使用 PED 的机率是 0.94。
而药检的准确度为95%。所谓准确度的定义是:如果一个球员使用了药物,他被检定为阳性的机率是 0.95;如果一个球员没有使用药物,他被检定为阴性的机率也是 0.95。也就是这里假设两种误差类型的机率 α 跟 β 都是 0.05。
问:当某个球员被检测出阳性时,他并不是 PED 使用者的反几率是多少?
根据题意画出表格,并且用贝叶斯公式进行计算:


如果大家对贝叶斯公式还是不太熟,可以用我前面说的混淆矩阵进行计算:

假设现在有10000人,即a+b+c+d=10000,
其中有6%的人使用了药物,剩下94%没有使用,即a+c=9400,b+d=600,
其中两类错误的概率均为0.05,即 a=0.05×9400=470, d=600×0.05=30,
剩下 c=9400×0.95=8930, b=600×0.95=570。
如图:

接下来我们要计算的是,在检测为阳性(P)的情况下,实际是未使用(N)的概率,即:
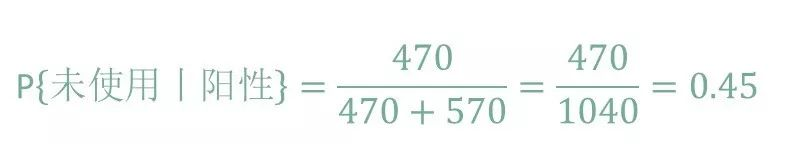
从结果来看,我们可以惊讶地发现,伪阳性的反几率可以高达45 %!也就是说,尽管药检的准确率已经很高了,高达了95%,但是当你被测出阳性出,仍然有45%的希望可以翻盘!
也就是说,大家做健康检查的时候,如果医生说,你的检查结果呈阳性,大家先不要慌张,而是勇敢地甩出反问三连:得这种病的先验概率是多少?检验的准确率是多少,如果一个真正有这种病的人来检定,呈现伪阳性的概率有多少?如果一个没有病的人来检定,呈现伪阴性的概率是多少?
然后你就可以自己计算出伪阳性的反几率,医学上很多疾病,在所有人口里面,得病的比例通常很小的,也就是说,得病的先验机率通常都很小,所以这个反几率通常会很大。
假设检验中的贝叶斯定理
现在用这个表格表示我们的p值统计检定,如下图,与前面的很像,只是将真实值为阴性阳性改为虚无假设是真的、或是假的;预测值改为统计检定是显著、或是不显著的。然后再加上一行先验机率,就是"虚无假设是对的"的先验机率有多少、"虚无假设是错的"的先验机率有多少。

其中,犯第一类错误的概率α在统计学中也称为显著性水平或统计水准,是我们人为设定;1-犯第二类错误的概率β=power,称为检验强度。
用贝叶斯公式计算伪阳性的反几率:

可以得到,伪阳性的反几率是关于统计水准 α、检定强度(power = 1 - β)、和研究假设之先验机率(Pr(HA))的函数。
伪阳性反几率的影响因素

根据下面两个图,我们可以得出一些结论:


检验水准α一定时:
检验强度越大(β越小),伪阳性反机率越小
研究假设的先验机率越大,伪阳性反机率越小
这里有一个表格,列出了研究假设的先验机率,从最小排列到最大,可以看到在不同检定强度之下,伪阳性的反机率是多少。

从表中我们可以看到,研究假设的先验机率很小时,即使p值很显著,虚无假设仍为真的概率还是很高(可以将近1)!
当研究假设的先验机率为0.5时(即事先不知道哪一个是正确的,没有任何偏好的,例如丢铜板,两面的概率完全是随机的),伪阳性的反机率才能降到0.05(同α一样)。
当研究假设的先验机率很低时,可能严重低估了伪阳性的反机率,即使在P值很显著的情况下,H0仍为真的概率可能远大于α。
表格的第一列表示power=0.95,第二列power=0.75,第三列power=0.50,可以看到结果是差不多的,可见power对伪阳性的反几率作用不是那么强。
结论:研究假设的先验机率对于伪阳性反机率的作用较强,而检验强度(1-β)影响不大。
四、总结
5句大白话总结——p值为什么很危险!
现在我抛开所有的专业术语,用5句大白话进行总结:
①P值告诉我们的是:H0为真的情况下,观察值出现的可能性大小,即 a/(a+c)


②作为研究者实际想知道的是:出现某个观察值之后,H0为真的,即 a/(a+b)


③两者当且仅当a=0时才会相等,但是a绝对不可能为0,否则就不是统计了
④如果要求②,除了可以人为控制的a,还必须要知道b,而b往往是不知道的!
⑤P值检验中,我们用c代替了b,所以我们做出的统计推论很!可!能!是!错!误!的!
---本文完---