参考马春鹏 《模式识别与机器学习》翻译
使⽤概率分布的图形表⽰进⾏分析很有好处。这种概率分布的图形表⽰被称为概率图模型(probabilistic graphical models)。这些模型提供了⼏个有⽤的性质:
它们提供了⼀种简单的⽅式将概率模型的结构可视化,可以⽤于设计新的模型
通过观察图形,我们可以更深刻地认识模型的性质,包括条件独⽴性质。
⾼级模型的推断和学习过程中的复杂计算可以根据图计算表达,图隐式地承载了背后的数
两大类别
贝叶斯⽹络(Bayesian network),也被称为有向图模型(directed graphical model)
马尔科夫随机场(Markov random fields),也被称为⽆向图模型(undirected graphical models)
为了求解推断问题,通常⽐较⽅便的做法是把有向图和⽆向图都转化为⼀个不同的表⽰形式,被称为因⼦图 (factor graph)。
⾸先考虑三个变量a, b, c上的⼀个任意的联合分布p(a, b, c)。可以将联合概率分布写成下⾯的形式。
p
(
a
,
b
,
c
)
=
p
(
c
∣
a
,
b
)
p
(
a
,
b
)
p ( a , b , c ) = p ( c | a , b ) p ( a , b )
p ( a , b , c ) = p ( c ∣ a , b ) p ( a , b )
再次使⽤乘积规则
p
(
a
,
b
,
c
)
=
p
(
c
∣
a
,
b
)
p
(
b
∣
a
)
p
(
a
)
p ( a , b , c ) = p ( c | a , b ) p ( b | a ) p ( a )
p ( a , b , c ) = p ( c ∣ a , b ) p ( b ∣ a ) p ( a )
对于⼀个有K个结点的图,联合概率为
p
(
x
)
=
∏
k
=
1
K
p
(
x
k
∣
p
a
k
)
p ( \boldsymbol { x } ) = \prod _ { k = 1 } ^ { K } p \left( x _ { k } | \mathrm { pa } _ { k } \right)
p ( x ) = k = 1 ∏ K p ( x k ∣ p a k )
其中, pak表⽰xk的⽗结点的集合
多变量概率分布的⼀个重要概念是条件独⽴(conditional independence)(Dawid, 1980)。考虑三个变量a, b, c,并且假设给定b, c的条件下a的条件概率分布不依赖于b的值,即
p
(
a
∣
b
,
c
)
=
p
(
a
∣
c
)
p(a | b, c) = p(a | c)
p ( a ∣ b , c ) = p ( a ∣ c )
给定c的条件下,a条件独⽴于b。如果我们考虑以c为条件下的a, b的联合分布,我们可以⽤⼀种稍微不同的⽅式表⽰,即
p
(
a
,
b
∣
c
)
=
p
(
a
∣
b
,
c
)
p
(
b
∣
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
p(a, b | c) = p(a | b, c)p(b | c) \\ = p(a | c)p(b | c)
p ( a , b ∣ c ) = p ( a ∣ b , c ) p ( b ∣ c ) = p ( a ∣ c ) p ( b ∣ c )
我们有时会使⽤条件独⽴的⼀种简洁记号(Dawid, 1979),即
a
!
b
∣
c
a !b | c
a ! b ∣ c
联合概率分布的条件独⽴性可以直接从图中读出来,不⽤进⾏任何计算。完成这件事的⼀般框架被称为“d-划分”(d-separation),其中“d”表⽰“有向(directed)”(Pearl, 1988)。这⾥,我们⾮形式化地介绍了d-划分的概念,给出了d-划分准则的⼀个⼀般叙述。形式化的证明可以参考Lauritzen(1996)。
使⽤公式(8.5)给出的⼀般结果,对应于这个图的联合概率分布很容易写出来,即
p
(
a
,
b
,
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
p
(
c
)
p(a, b, c) = p(a | c)p(b | c)p(c)
p ( a , b , c ) = p ( a ∣ c ) p ( b ∣ c ) p ( c )
那么我们可以通过对公式(8.23)两边进⾏积分或求和的⽅式,考察a和b是否是相互独⽴的,即
p
(
a
,
b
)
=
∑
c
(
a
∣
c
)
p
(
b
∣
c
)
p
(
c
)
p(a, b) = \sum_{c} (a | c)p(b | c)p(c)
p ( a , b ) = c ∑ ( a ∣ c ) p ( b ∣ c ) p ( c )
这不能分解为乘积p(a)p(b),因此不独立。
现在假设我们以变量c为条件,如图8.16所⽰。根据公式(8.23),我们可以很容易地写出给
p
(
a
,
b
∣
c
)
=
p
(
a
,
b
,
c
)
p
(
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
\begin{aligned} p ( a , b | c ) & = \frac { p ( a , b , c ) } { p ( c ) } \\ & = p ( a | c ) p ( b | c ) \end{aligned}
p ( a , b ∣ c ) = p ( c ) p ( a , b , c ) = p ( a ∣ c ) p ( b ∣ c )
因此我们可以得到条件独⽴性质
a
⊥
b
∣
c
a \perp b | c
a ⊥ b ∣ c
当我们以结点c为条件时(如图8.16所⽰),被⽤作条件的结点“阻隔”了从a到b的路径,使得a和b变得(条件)独⽴了。
当我们以结点c为条件时(如图8.16所⽰),被⽤作条件的结点“阻隔”了从a到b的路径,使得a和b变得(条件)独⽴了。
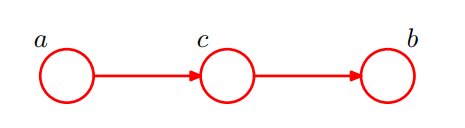
p
(
a
,
b
,
c
)
=
p
(
a
)
p
(
c
∣
a
)
p
(
b
∣
c
)
p ( a , b , c ) = p ( a ) p ( c | a ) p ( b | c )
p ( a , b , c ) = p ( a ) p ( c ∣ a ) p ( b ∣ c )
我们可以考察a和b是否是相互独⽴的,⽅法是对c积分或求和,结果为,很明显不独立
p
(
a
,
b
)
=
p
(
a
)
∑
c
p
(
c
∣
a
)
p
(
b
∣
c
)
=
p
(
a
)
p
(
b
∣
a
)
p ( a , b ) = p ( a ) \sum _ { c } p ( c | a ) p ( b | c ) = p ( a ) p ( b | a )
p ( a , b ) = p ( a ) c ∑ p ( c ∣ a ) p ( b ∣ c ) = p ( a ) p ( b ∣ a )
现在假设我们以结点c为条件,其是独立的
p
(
a
,
b
∣
c
)
=
p
(
a
,
b
,
c
)
p
(
c
)
=
p
(
a
)
p
(
c
∣
a
)
p
(
b
∣
c
)
p
(
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
\begin{aligned} p ( a , b | c ) & = \frac { p ( a , b , c ) } { p ( c ) } \\ & = \frac { p ( a ) p ( c | a ) p ( b | c ) } { p ( c ) } \\ & = p ( a | c ) p ( b | c ) \end{aligned}
p ( a , b ∣ c ) = p ( c ) p ( a , b , c ) = p ( c ) p ( a ) p ( c ∣ a ) p ( b ∣ c ) = p ( a ∣ c ) p ( b ∣ c )
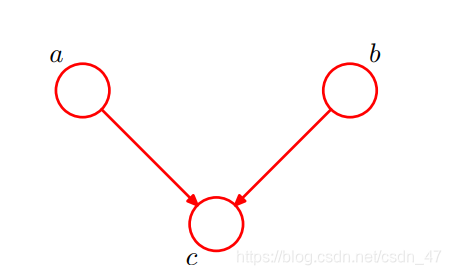
再考虑另一个图
p
(
a
,
b
,
c
)
=
p
(
a
)
p
(
b
)
p
(
c
∣
a
,
b
)
p ( a , b , c ) = p ( a ) p ( b ) p ( c | a , b )
p ( a , b , c ) = p ( a ) p ( b ) p ( c ∣ a , b )
两侧关于c积分或求和,我们有,是独立的
p
(
a
,
b
)
=
p
(
a
)
p
(
b
)
p ( a , b ) = p ( a ) p ( b )
p ( a , b ) = p ( a ) p ( b )
假设我们以c为条件,并不是独立的
p
(
a
,
b
∣
c
)
=
p
(
a
,
b
,
c
)
p
(
c
)
=
p
(
a
∣
c
)
p
(
b
∣
c
)
p
(
c
∣
a
,
b
)
p
(
c
)
\begin{aligned} p ( a , b | c ) & = \frac { p ( a , b , c ) } { p ( c ) } \\ & = \frac { p ( a | c ) p ( b | c ) p ( c | a , b ) } { p ( c ) } \end{aligned}
p ( a , b ∣ c ) = p ( c ) p ( a , b , c ) = p ( c ) p ( a ∣ c ) p ( b ∣ c ) p ( c ∣ a , b )
考虑⼀个⼀般的有向图,其中A, B, C是任意⽆交集的结点集合,我们考虑从A中任意结点到B中任意结点的所有可能的路径。我们说这样的路径被“阻隔”,如果它包含⼀个结点满⾜下⾯两个性质中的任何⼀个。
路径上的箭头以头到尾或者尾到尾的⽅式交汇于这个结点,且这个结点在集合C中。
箭头以头到头的⽅式交汇于这个结点,且这个结点和它的所有后继都不在集合C中。
如果所有的路径都被“阻隔”,那么我们说C把A从B中d-划分开,且图中所有变量上的联合概率
A
⊥
B
∣
C
A \perp B | C
A ⊥ B ∣ C
⼀个马尔科夫随机场(Markov random field),也被称为马尔科夫⽹络(Markov network)