问题描述:

解答:
class Solution {
public String longestPalindrome(String s) {
int len=s.length();
if(len<2){
return s;
}
int maxLen=0;
int start=0;
for(int i=0;i<len-1;i++){
int left=i,right=i;
while(left>=0 && right<=len-1 && s.charAt(left)==s.charAt(right)){
left--;
right++;
}
if(maxLen<right-left-1){
maxLen=right-left-1;
start=left+1;
}
left=i;right=i+1;
while(left>=0 && right<=len-1 && s.charAt(left)==s.charAt(right)){
left--;
right++;
}
if(maxLen<right-left-1){
maxLen=right-left-1;
start=left+1;
}
}
return s.substring(start,start+maxLen);//左闭右开
}
}接下来补上manacher算法。
在没了解Manacher之前,我们可以直接暴力枚举,时间复杂度O(n3),也可以用聪明一点的方法,每次枚举一个点,比较它左右距离相同的点是否相同,时间复杂度O(n2)
不过
Manacher时间复杂度为O(n)。
下面正式开始分析算法
首先,我们需要了解一个叫做回文半径的东西
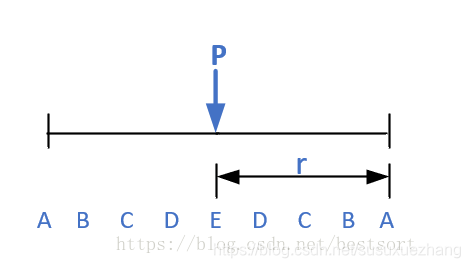
如上图,P点为中心点,ABCDEDCBA构成一个回文串,那么rr的长度就是该回文串的回文半径
我们都知道,中心检测法是依次枚举每一个点的回文半径,取所有回文半径的最大值.当当前字符满足回文条件的时候,检测下一个字符,否则返回当前半径长度,然后回文半径长度回退为1开始检测下一点.但是这个回退是可以避免的
这里用图解的形式解释一下:
先设之前已经匹配好了的最大回文半径长为R,然后设当前点的回文半径为r,其中,rr的起点一定大于R的起点(因为处理r的时候R已经处理好了)
那么R和r的关系一定有如下3种情况
1.r右端点<=R右端点&&r左端点>=R中心点**,如图示这种情况
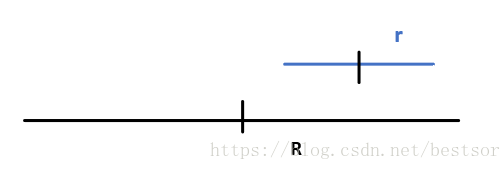
我们这里先给出r段关于R中心点所对称的线段r1

因为r和r1是关于R中心点对称的,所以r的回文半径一定等于r1
对于此种情况,可以从图中看出来r的回文半径一定小于R的回文半径,因为图中以蓝色竖线为起点包含的字符数小于以黑色竖线为起点所包含的字符数.所以这种情况下,回文半径最大值仍为R
2.右端点< R右端点&&r左端点< R中心点,如下图 
还是和1一样,我们先画出关于R中心点对称的r1

我们在这副图中也能找到对称的线段,如下图

红色和红色对对称,蓝色和蓝色对称,所以,r和r1仍然关于R中心点对称,也就是r的回文半径依旧等于r1的回文半径.
3.r右端点>R右端点

还是和上面一样处理成下图

靠下的蓝色虚线+蓝色实线+黄色实线=之前的r蓝色虚线+蓝色实线+黄色实线=之前的r
有了上面的基础,我们现在唯一需要查询的就是黄线部分了,这里将回文半径由RR继续扩大就好
到此,原理说完了,我们来看看代码怎么写的吧
先放上原作者伪码
/*
String:加'#'处理后的回文串
MaxR:最长回文半径
flag:最长回文半径对应的中心点下标
cnt[i]:以i为中心对应的回文半径
length:String长度
*/
for i to length
if MaxR > i: //如果当前点被最长回文半径包含
cnt[i]=min(cnt[2*flag-i],MaxR-i) //取情况1和情况2中较小的(防止超出MaxR范围)
else:
cnt[i]=1
while(String[i+cnt[i]] == String[i-cnt[i]]):
cnt[i]++;
if i+cnt[i] > MaxR:
MaxR=i+cnt[i],flag=i;
下面上作者正式代码
void Manacher(char s[],int len) {//原字符串和串长
int l = 0;
String[l++] = '$'; // 0下标存储为其他字符,防止越界
String[l++] = '#';
for (int i = 0; i < len; i++) {
String[l++] = s[i];
String[l++] = '#';
}
String[l] = 0; // 空字符
int MaxR = 0;
int flag = 0;
for (int i = 0; i < l; i++) {
cnt[i] = MaxR > i ? min(cnt[2 * flag - i], MaxR - i) : 1;//2*flag-i是i点关于flag的对称点
while (String[i + cnt[i]] == String[i - cnt[i]])
cnt[i]++;
if (i + cnt[i] > MaxR) {
MaxR = i + cnt[i];
flag = i;
}
}
}
/*
* String: $ # a # b # a # a # b # a # 0
* cnt: 1 1 2 1 4 1 2 7 2 1 4 1 2 1
*/
本人复现代码:
class Solution {
public String longestPalindrome(String s) {
if(s==null||s.length()<=1)
return s;
String t = "#";
for (int i = 0; i < s.length(); ++i) {
t += s.charAt(i);
t += "#";
}
// Process t
int [] p=new int[t.length()];
int mx = 0, id = 0, resLen = 0, resCenter = 0;
for (int i = 0; i < t.length(); ++i) {
p[i] = mx > i ? Math.min(p[2 * id - i], mx - i) : 1;
while (i - p[i] >= 0 && i + p[i] < t.length() && t.charAt(i + p[i]) == t.charAt(i - p[i])){
p[i]++;
}
if (mx < i + p[i]) {
mx = i + p[i];
id = i;
}
if (resLen < p[i]) {
resLen = p[i];
resCenter = i;
}
}
return s.substring((resCenter - (resLen-1))/ 2,(resCenter + (resLen-1))/ 2);
}
}return那一句调试了很久,记录一下过程
resLen-1为实际回文串长度
resCenter为t中回文串的中心点
t中回文串是 [ resCenter - (resLen-1) , resCenter + (resLen-1) ] 左右都是闭区间
s中回文串是 [ (resCenter - (resLen-1))/ 2, (resCenter + (resLen-1))/ 2 ) 左闭又开
原文链接:https://blog.csdn.net/bestsort/article/details/81637464