高数第八章题型总结

1. 两点之间的距离

已知 $A(x_1,y_1,z_1)$， $B(x_2,y_2,z_2)$，两点之间的距离为 $d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

2.点到平面的距离

已知平面 $\Pi:Ax+By+Cz+D=0$，则点 $M_0(x_0,y_0,z_0)$到平面的距离为
$d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$

3.平行平面之间的距离

平面 $\Pi_1:Ax+By+Cz+D_1=0$，平面 $\Pi_2:Ax+By+Cz+D_2=0$，两平面之间的距离为
$d=\frac{|D_2-D_1|}{\sqrt{A^2+B^2+C^2}}$

4.点到直线的距离

点 $M_0(x_0,y_0,z_0)$，到直线 $L:\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}$的距离
1.方法一：
①过点 $M_0$作垂直于直线 $L$的平面 $\Pi:m(x-x_0)+n(y-y_0)+p(z-z_0)=0$
②求 $\Pi$和直线 $L$的交点 $M_1(x_1,y_1,z_1)$，注：把直线转换为参数式带入平面方程得到 $M_1$的坐标
③ $d=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2+(z_1-z_0)^2}$
2.方法二：

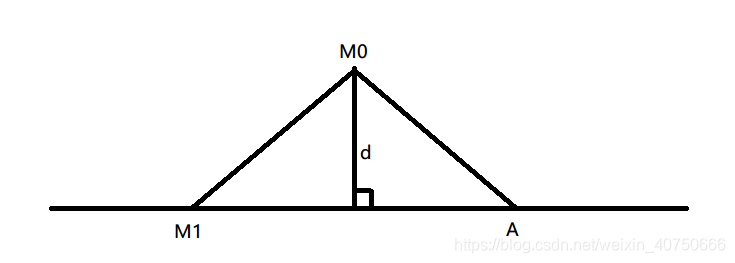
任取直线上一点 $M_1(x_1,y_1,z_1)$，连接 $M_0M_1$，以 $M_1$为起点作一条平行于直线的向量 $\overrightarrow{M_1A}=\vec n=(m,n,p)$,由于 $S_{\triangle{M_0M_1A}}=\frac{1}{2}\cdot|\overrightarrow{M_1A}\times\overrightarrow{M_1M_0}|=\frac{1}{2}\cdot d\cdot|\overrightarrow{M_1A}|$因此 $d=\frac{|\overrightarrow{M_1A}\times\overrightarrow{M_1M_0}|}{|\overrightarrow{M_1A}|}=\frac{|\vec n\times\overrightarrow{M_1M_0}|}{|\vec n|}$

5.异面直线之间的距离

已知直线： $L_1:\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1}$和 $L_2:\frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2}$，则直线上两点为 $m_1(x_1,y_1,z_1)$和 $m_2(x_2,y_2,z_2)$
$L_1$和 $L_2$共面的充要条件为： $\vec L_1 \times \vec L_2 \cdot \overrightarrow{m_1m_2}=0$
$L_1$和 $L_2$异面的充要条件为： $\vec L_1 \times \vec L_2 \cdot \overrightarrow{m_1m_2} \neq 0$
当两直线异面时，需要转化为两直线共面的问题来解答

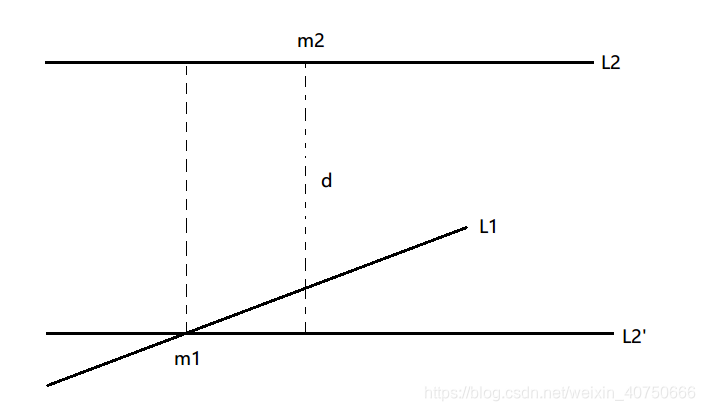
①过 $m_1$做平行于 $L_2$的直线 $L_2'$
②求 $m_2$到直线 $L_2'$之间的距离 $d$
③求两共面直线的距离可以转化为求点到直线的距离的问题。
注：上图中求 $m_2$到直线 $L_2'$的距离即可使用上述第二种方法用 $L_2'$的方向向量 $\vec n=(m_2,n_2,p_2)\times \overrightarrow{m_1m_2}$再除以 $|\vec n|$