1、拉格朗日插值法

①原理

对于平面上已知的n个点，可以找到一个n-1次多项式y=a₀+a₁x+a₂x²+…+a_n-1x^n-1，使得该多项式曲线经过这n个点。对于缺失的值，将对应的x值代入多项式即可得到近似值L(x)。

②公式推算

已知：

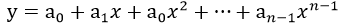
将n个点的坐标(x_i,y_i)代入多项式，得：

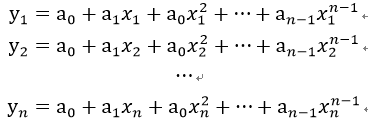
解得拉格朗日插值多项式为：

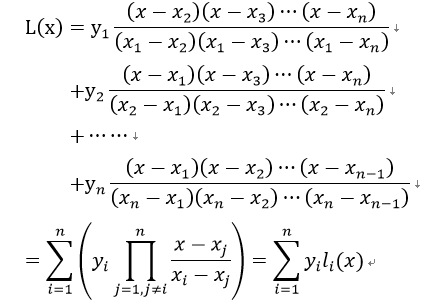
拉格朗日插值公式是在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值。

缺点：

1、在计算中，当插值点增加或减少一个时，所对应的基本多项式就需要全部重新计算，于是整个公式都会变化，非常繁琐。计复杂度为O(n²)。

2、当插值点比较多的时候，拉格朗日插值多项式的次数可能会很高，因此具有数值不稳定的特点，也就是说尽管在已知的几个点取到给定的数值，但在附近却会和“实际上”的值之间有很大的偏差（如右下图）[6]。这类现象也被称为龙格现象，解决的办法是分段用较低次数的插值多项式。

③改进——重心拉格朗日插值

不妨设：

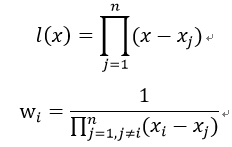
其中w_i称为重心权，则改进后：

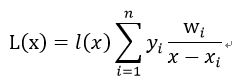
优点：

1、当数据点的个数增加一个x_n+1时，可在O(n)复杂度内更新每个w_i(w_i←w_i/(x_i-x_n+1))，以及计算新的重心权w_n+1，并在O(n)时间内计算得到新的L(x)。

2、牛顿插值法

①原理

牛顿（Newton）插值公式是代数插值方法的一种形式。牛顿差值引入了差商的概念，使其在差值节点增加时便于计算。

②公式推演

求已知的n个点对(x_i,y_i)的所有阶的差商公式：

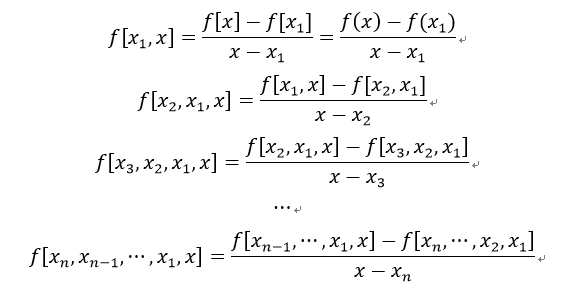
变换得到：

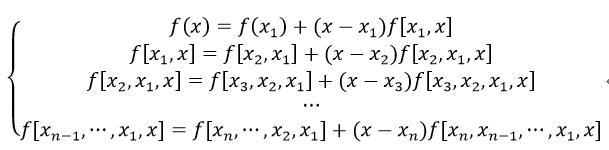
然后其中1式+(x-x1)·2式+···+(x-x₁)···(x-x_n-1)·n式，得到：

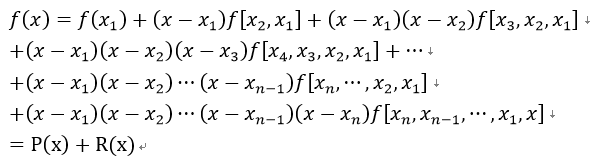
其中：

P(x)称为牛顿插值逼近函数，R(x)称为误差函数。

1、对于P(x)，每当新增一个插值数据点，前面已有的各项不变，计算只增加一项。每项系数均为各阶差商。

2、仍没有改变拉格朗日的插值曲线在节点处有尖点，不光滑，插值多项式在节点处不可导等缺点。

埃尔米特插值是另一类插值问题，这类插值在给定的节点处，不但要求插值多项式的函数值与原函数值相同。同时还要求在节点处，插值多项式的一阶直至指定阶的导数值，也与被插函数的相应阶导数值相等。

样条插值法是一种以可变样条来作出一条经过一系列点的光滑曲线的数学方法。插值样条是由一些多项式组成的，每一个多项式都是由相邻的两个数据点决定的，这样，任意的两个相邻的多项式以及它们的导数(不包括仇阶导数)在连接点处都是连续的。