拓扑排序
在一个有向图中,对所有的节点进行排序,要求没有一个节点指向它前面的节点。
先统计所有节点的入度,对于入度为0的节点就可以分离出来,然后把这个节点指向的节点的入度减一。
一直做改操作,直到所有的节点都被分离出来。
如果最后不存在入度为0的节点,那就说明有环,不存在拓扑排序,也就是很多题目的无解的情况。
欧拉回路
什么是欧拉路径?在图上用一种走法经过所有的边一次且只有一次的路径叫做欧拉路径。即一笔画。
如果这条路径的起点和终点重合,那么就是欧拉回路。
如何判断图是否有欧拉回路或者欧拉路径?
无向图:因为欧拉路径中,除了起点与终点以外,任意点的“进”“出”次数相等,所以除了两个点为奇点(度数为奇数的点)(终点和起点)以外,其它点的度数均为偶数。
如果是欧拉回路,奇点的个数应该为0。
有向图:欧拉路径中,最多只有两个点的入度不等于出度。起点出度比入度大1,终点入度比出度大1。
如果是欧拉回路,所有点的 入度=出度 。
寻找欧拉回路或欧拉路径的算法有?
Fluery算法和Hierholzer算法。后者好像也有博客称逐步插入回路法。
后面一种算法无论是编程复杂度还是时间复杂度好像都比前种算法复杂度更优,但前者的应用广泛性好像比后者更高。欧拉回路的更高级的应用还没涉及,如果之后有什么新内容再来补充吧....所以这里就用Hierholzer算法了。
Hierholzer算法自动寻找欧拉回路,在找不到欧拉回路的情况下会找到欧拉路径。前提是得给它指定好起点。
算法流程(无向图):
1.判断奇点数。奇点数若为0则任意指定起点,奇点数若为2则指定起点为奇点。
2.开始递归函数Hierholzer(x):
循环寻找与x相连的边(x,u):
删除(x,u)
删除(u,x)
Hierholzer(u);
将x插入答案队列之中
3.倒序输出答案队列
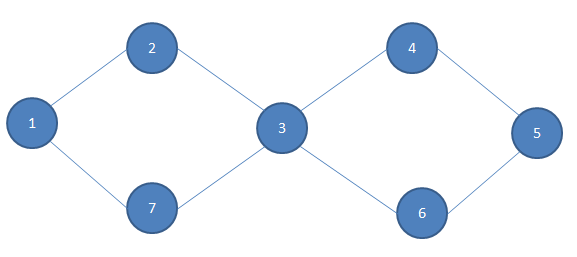
对于该图,算法的执行流程如下:
1.找到该图没有奇点,从1开始进行Hierholzer算法。
2.删边1-2 递归到2
3.删边2-3 递归到3
4.删边3-7 递归到7
5.删边7-1 递归到1
6.1无边,1加入队列,返回
7.7加入队列,返回
8.删边3-4 递归到4
9.删边4-5 递归到5
10.删边5-6 递归到6
11.删边6-3 递归到3
12.3加入队列,返回
13.6加入队列,返回
14.5加入队列,返回
15.4加入队列,返回
16.3加入队列,返回
17.2加入队列,返回
18.1加入队列,返回
答案队列为:1 7 3 6 5 4 3 2 1。反向输出即为答案。
有向图除判断是否存在有一点点不同以外同理。