开根号的几类算法总结

首先是最基本的二分开根号，这个比较容易理解，复杂度比起下面讲的牛顿迭代法要高，更容易理解。
下面给出代码：

#define eps 0.00001
float SqrtByDichotomy(float n)
{
if(n<0)
{
return -1.0;
}
else
{
float low,up,mid,last;
low=0,up=(n>=1?n:1);
mid=(low+up)/2;

do
{
if(mid*mid>n)
up=mid;
else
low=mid;

last=mid;
mid=(up+low)/2;

}while(fabsf(mid-last) > eps); //求浮点数x的绝对值

return mid;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
牛顿迭代法
这个算法的复杂度比二分法低。
牛顿迭代法——百度百科里面讲的很清楚。

http://baike.baidu.com/view/643093.htm

设r是的根，选取作为r的初始近似值，过点做曲线的切线L，L的方程为，求出L与x轴交点的横坐标，称x1为r的一次近似值。过点做曲线的切线，并求该切线与x轴交点的横坐标，称为r的二次近似值。重复以上过程，得r的近似值序列，其中，称为r的次近似值，上式称为牛顿迭代公式。

如果只是开根号运算的话，迭代公式为：

double SQR(double a){
double x=a,y=0.0;
while(fabs(x-y)>0.00001){
y=x;
x=0.5*(x+a/x);
}
return x;
}

还有其他算法先不看了，感觉把这两种弄明白差不多了，有一种Carmack算法精度不够，但是复杂度低，感兴趣的时候可以看看。
---------------------
作者：th是个小屁孩
来源：CSDN
原文：https://blog.csdn.net/u013775952/article/details/51452855
版权声明：本文为博主原创文章，转载请附上博文链接！

作者：黄徐升
链接：https://www.zhihu.com/question/20690553/answer/543620219
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

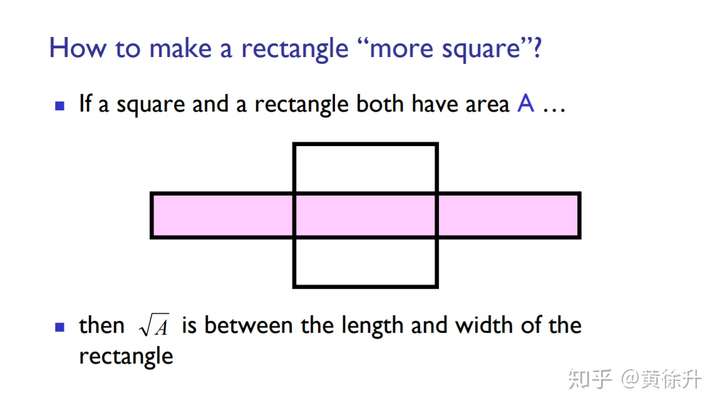
有一个利用“将长方形变得更像正方形”的思路也可以得到求 $A$ 的算数平方根的迭代公式

$x_{k+1}=\dfrac{1}{2}\left( x_{k}+\dfrac{A}{x_k} \right)\\$

算是通俗易懂地得到了这个迭代公式（不过并没有体现牛顿法的求导等过程，那个用抛物线的切线看是比较直观的，别的回答里已经有了）。

首先是考虑 $\sqrt{A}$ 是面积为 $A$ 的正方形的边长，如果画一个邻边不等的面积是 $A$ 长方形，设这个长方形的长为 $L$ ，宽为 $A/L$ ，那么怎样能让这个长方形变得更像一个正方形呢？是要把长变得短一点，宽变得长一点，可以用长和宽的平均数 $(L+A/L)/2$ 来作为新的长 $L_{new}$ ，在面积不变的条件下，新的宽是 $A/L_{new}$ 。这样不断操作下去，长方形的长和宽会越来越接近，就是一直趋近与 $\sqrt{A}$ 了。