样本相似性度量（欧几里得距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、标准化欧氏距离）

版权声明：转载请写明出处，谢谢！ https://blog.csdn.net/wilson1068/article/details/86721003

样本相似性度量（欧几里得距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、标准化欧氏距离）

在分类过程中，常常需要估算不同样本直接的 Similarity Measurement （相似性度量）。

此时常用的方法就是计算两个样本直接的 Distance（距离）。

常用方法有：

• 1. 欧几里得距离（Euclidean Distance）
• 2. 曼哈顿距离（Manhattan Distance）
• 3. 切比雪夫距离（Chebyshev Distance）
• 4. 闵可夫斯基距离（Minkowski Distance）
• 5. 标准化欧氏距离（Standardized Euclidean distance）

1. 欧几里得距离（Euclidean Distance）

欧几里得距离（Euclidean Distance），简称欧氏距离，又称欧几里得度量（euclidean metric）。

指 m 维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

在欧几里得空间中，点 $x=\left(x_{1}, \cdots, x_{n}\right)$ 和 $y=\left(y_{1}, \cdots, y_{n}\right)$ 之间的欧几里得距离为：

$d(x, y) :=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}}$

当 $y$ 点为原点时，即为向量 $\vec{x}$ 的自然长度（该点到原点的距离）。

向量 $\vec{x}$ 的自然长度：

$\|\vec{x}\|_{2}=\sqrt{\left|x_{1}\right|^{2}+\cdots+\left|x_{n}\right|^{2}}$

由 $n$ 维空间的欧几里得距离公式可以推出：

二维平面上两点 $a\left(x_{1},y_{1}\right)$ 与 $b\left(x_{2},y_{2}\right)$ 间的欧几里得距离：

$d_{12}=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}$

三维空间两点 $a\left(x_{1}, y_{1}, z_{1}\right)$ 与 $b\left(x_{2},y_{2}, z_{2}\right)$ 间的欧几里得距离：

$d_{12}=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}}$

2. 曼哈顿距离（Manhattan Distance）

计程车几何 (Taxicab geometry) 或曼哈顿距离 (Manhattan distance or Manhattan length) 或方格线距离是由十九世纪的赫尔曼 · 闵可夫斯基所创辞汇，为欧几里得几何度量空间的几何学之用语，用以标明两个点上在标准坐标系上的绝对轴距之总和。

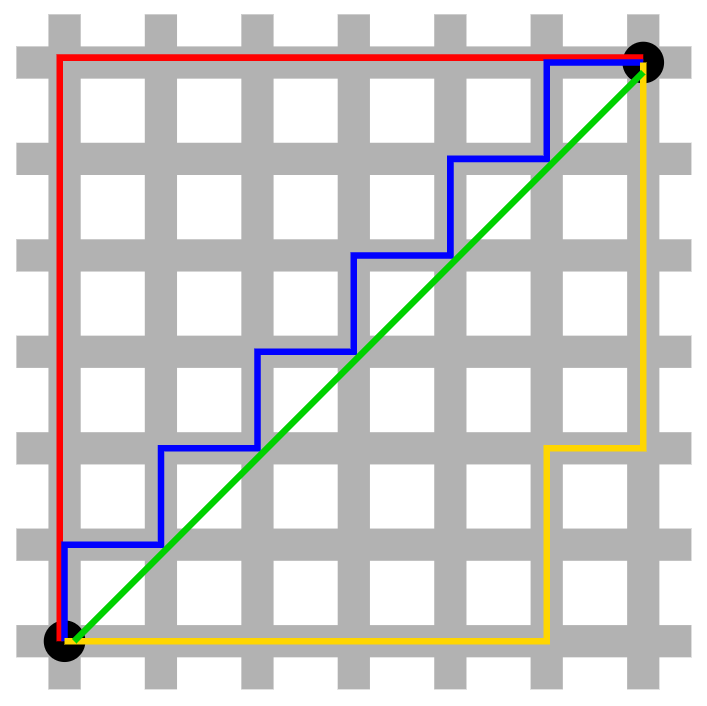
如上图，从右上角的黑点到左下角的黑点的最小距离是？

是红色线的欧几里得距离？

显然是错误的。在这样的空间里，欧几里得距离计算最小距离是不合适的。

需要采用新的距离计算方式 —— 曼哈顿距离

在 N 维空间中，点 $x=\left(x_{1}, \cdots, x_{n}\right)$ 和 $y=\left(y_{1}, \cdots, y_{n}\right)$ 之间的曼哈顿距离为：

$d(x, y) :=\left|x_{1}-y_{1}\right|+\left|x_{2}-y_{2}\right|+\cdots+\left|x_{n}-y_{n}\right|=\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|$

二维平面两点 $a\left(x_{1},y_{1}\right)$ 与 $b\left(x_{2},y_{2}\right)$ 间的曼哈顿距离：

$d_{12} :=\left|x_{1}-y_{1}\right|+\left|x_{2}-y_{2}\right|$

3. 切比雪夫距离（Chebyshev Distance）

在 $n$ 维空间中，点 $x=\left(x_{1}, \cdots, x_{n}\right)$ 和 $y=\left(y_{1}, \cdots, y_{n}\right)$ 之间的切比雪夫距离为：

$d(x, y) :=\max_{i}\left(\left|x_{i}-y_{i}\right|\right)$

二维平面两点 $a\left(x_{1},y_{1}\right)$ 与 $b\left(x_{2},y_{2}\right)$ 间的切比雪夫距离：

$d_{12} :=max\left(\left|x_{1}-y_{1}\right|,\left|x_{2}-y_{2}\right|\right)$

4. 闵可夫斯基距离（Minkowski Distance）

闵可夫斯基距离（Minkowski Distance），简称闵氏距离。

它是一组距离的定义。

设定两点：

$P=\left(x_{1}, x_{2}, \ldots, x_{n}\right) \text {and} Q=\left(y_{1}, y_{2}, \ldots, y_{n}\right) \in \mathbb{R}^{n}$

直接的闵可夫斯基距离为：

$\left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{p}\right)^{1 / p}$

那么 $p$ 的常用取值为 $1$ 或 $2$。

$p=1$ 即为曼哈顿距离：

$\left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{1}\right)^{\frac{1}{1}}=\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|$

$p=2$ 即为欧几里得距离：

$\left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{2}\right)^{\frac{1}{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}}$

$p\rightarrow \infty$ 取无穷时极限情况下可以得到切比雪夫距离：

$\lim _{p \rightarrow \infty}\left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{p}\right)^{\frac{1}{p}}=\max _{i=1}^{n}\left|x_{i}-y_{i}\right.$

5. 标准化欧氏距离（Standardized Euclidean distance）

标准欧氏距离的定义：

标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。

标准欧氏距离的思路：既然数据各维分量的分布不一样，好吧！那我先将各个分量都 “标准化” 到均值、方差相等吧。
均值和方差标准化到多少呢？
假设样本集 $X$ 的均值 (mean) 为 $m$，标准差(standard deviation)为 $s$，那么 $X$ 的 “标准化变量 $X^{*}$” 表示为：

而且标准化变量的数学期望为 $0$，方差为 $1$。因此样本集的标准化过程 (standardization) 用公式描述就是：

$X^{*}=\frac{X-m}{s}$

标准化后的值 = (标准化前的值 － 分量的均值) / 分量的标准差

经过简单的推导就可以得到两个 n 维向量 $a\left(x_{11}, x_{12}, \cdots, x_{1n}\right)$ 与 $b\left(x_{21}, x_{22}, \cdots, x_{2n}\right)$ 间的标准化欧氏距离的公式：

如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离 (Weighted Euclidean distance)。

$d_{12}=\sqrt{\sum_{k=1}^{n}\left(\frac{x_{1 k}-x_{2 k}}{s_{k}}\right)^{2}}$

如果使用长宽比为 $2:1$ 的二维矩形作为单元大小，那么使用标准欧式距离公式为：

$d=\sqrt{\left(\frac{x_{2}-x_{1}}{2}\right)^{2} + \left(\frac{x_{2}-x_{1}}{1}\right)^{2} }$