开头声明：树状数组 还是 没有 线段树 优越（理直气壮）
1、前言
这么简单的东西一直没有来看一眼。。。因为最初学数据结构的时候就曾从各方各面了解到线段树的各种优越性，各种比树状数组好，于是就看了线段树就没管了。。。但是树状数组的常数小，代码短这些隐性优势也许当时并不清楚吧。
2、概念
树状数组，依旧是一个线性数组构成，但是其性质却如同树结构一样是立体的。如图所示，我们首先给出一个最基本的a数组的一部分，大家可以观察一下上方的c数组有什么规律？
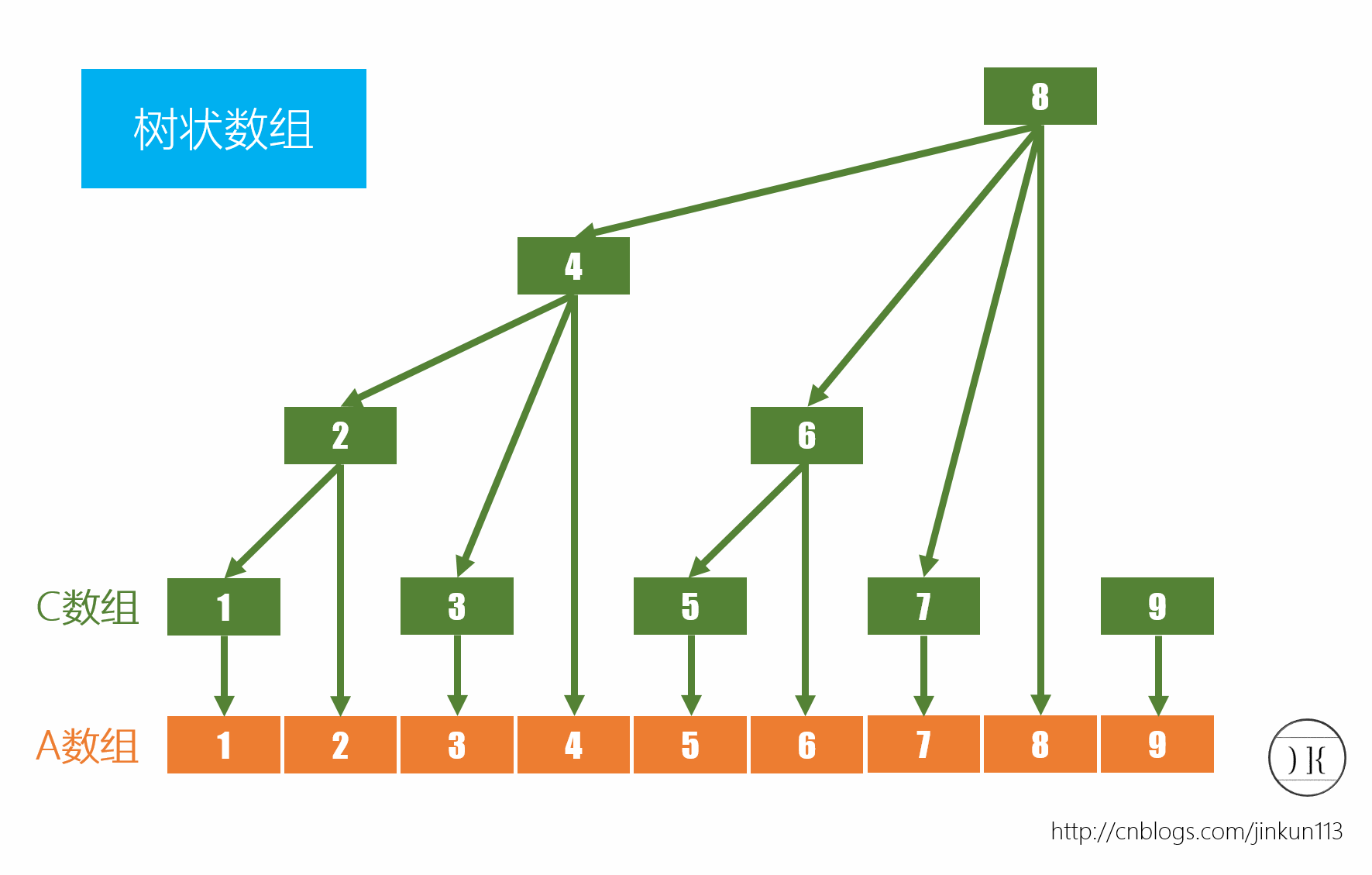我们将箭头看做该节点的儿子节点，每一个节点的权值为所有儿子节点的权值和，易得：
c[1]=a[1]；c[2]=a[1]+a[2]；c[3]=a[3]；c[4]=c[2]+a[3]+a[4]=a[1]+a[2]+a[3]+a[4]；
c[5]=a[5]；c[6]=a[5]+a[6]；c[7]=a[7]；c[8]=c[4]+c[6]+a[7]=a[1]+a[2]+...+a[8]。
没错，上方的c数组就是树状数组。分析数据之后，我们可以得到树状数组的一些性质：对于c[i]，他的儿子节点取决于i的所有因子中最多有2^j次幂，则向前取2^j个数作为儿子，即[i-2^j+1,i]。例如，6的最大2次方因子为2，即2^1，则向前取2个数，则c[6]=a[5]+a[6]；8的最大2次方因子为8，即2^3，则向前取8个数，则c[8]=a[1]+a[2]+...+a[8]。
3、构建&询问&修改
三个步骤，一起讲了吧，都很简单。
<1>构建：应该并不存在什么难度，唯一要考虑的就是如何得到为该数因子中最大的2^x是多少。我自己在想的时候只能想到很复杂的还要预处理的方式，其实巧妙地利用位运算符就可以以O（1）的速度直接得到，至于原因，没有去考虑，记着就行吧。代码：
------------------------------------------------------------------------------------------------------
int lowbit(int x) { return x&(-x); }
------------------------------------------------------------------------------------------------------
<2>求数组的和：我们注意到，树状数组在求和的时候，相对于普通数组的优势就像树链剖分和普通LCA一样。每次我们不需要一个一个相加，直接利用当前位置的lowbit值跳转即可，如代码：
------------------------------------------------------------------------------------------------------
int getSum(int now)
{
int sum=0;
while (now>0) sum+=c[now],now-=lowbit(now);
return sum;
}
------------------------------------------------------------------------------------------------------
<3>单点修改权值：同样地，修改也是非常快的，O（log n），假设当前为节点i加上val，如代码：
------------------------------------------------------------------------------------------------------
int update(int i,int val) { while (i<=n) c[i]+=x,i+=lowbit(i); }
------------------------------------------------------------------------------------------------------
4、总结
显然可以看出来了，树状数组空间复杂度小些，代码短些，常数也小些，这些平时可能不是很注意的优势都要注意，虽然它的功能缺失逊于线段树，但是在能够使用树状数组的情况下，我觉得还是可以多用用。