EM算法的适用场景:
- EM算法用于估计含有隐变量的概率模型参数的极大似然估计,或者极大后验概率估计。
- 当概率模型既含有观测值,又含有隐变量或潜在变量时,就可以使用EM算法来求解概率模型的参数。
- 当概率模型只含有观测值时,直接使用极大似然估计法,或者贝叶斯估计法估计模型参数就可以了。
最大似然估计:若X为离散型随机变量,其概率分布的形式为P{X=x}=p(x;theta). 当样本值确定时,所有样本的乘积可以看作是theta的函数,并称为似然函数。
由于已经得到了样本值(x1,…,xn),那它的出现的可能性应该是大的,即似然函数的值应该是大的。因而我们选择使似然函数达到最大值的那个theta做为真theta的估计
EM算法的入门简单例子:
已知有三枚硬币A,B,C,假设抛掷A,B,C出现正面的概率分别为pi,p,q。
单次实验的过程是:
1.首先抛掷硬币A,如果A出现正面选择硬币B,否则,选择硬币C。
2.抛掷所选择的硬币,正面输出1,反面输出0。
重复上述单词实验n次,需要估计抛掷硬币A,B,C出现正面的概率pi,p,q。
其中每次实验步骤1的抛掷结果不可见,可见的是所挑选硬币的抛掷结果。




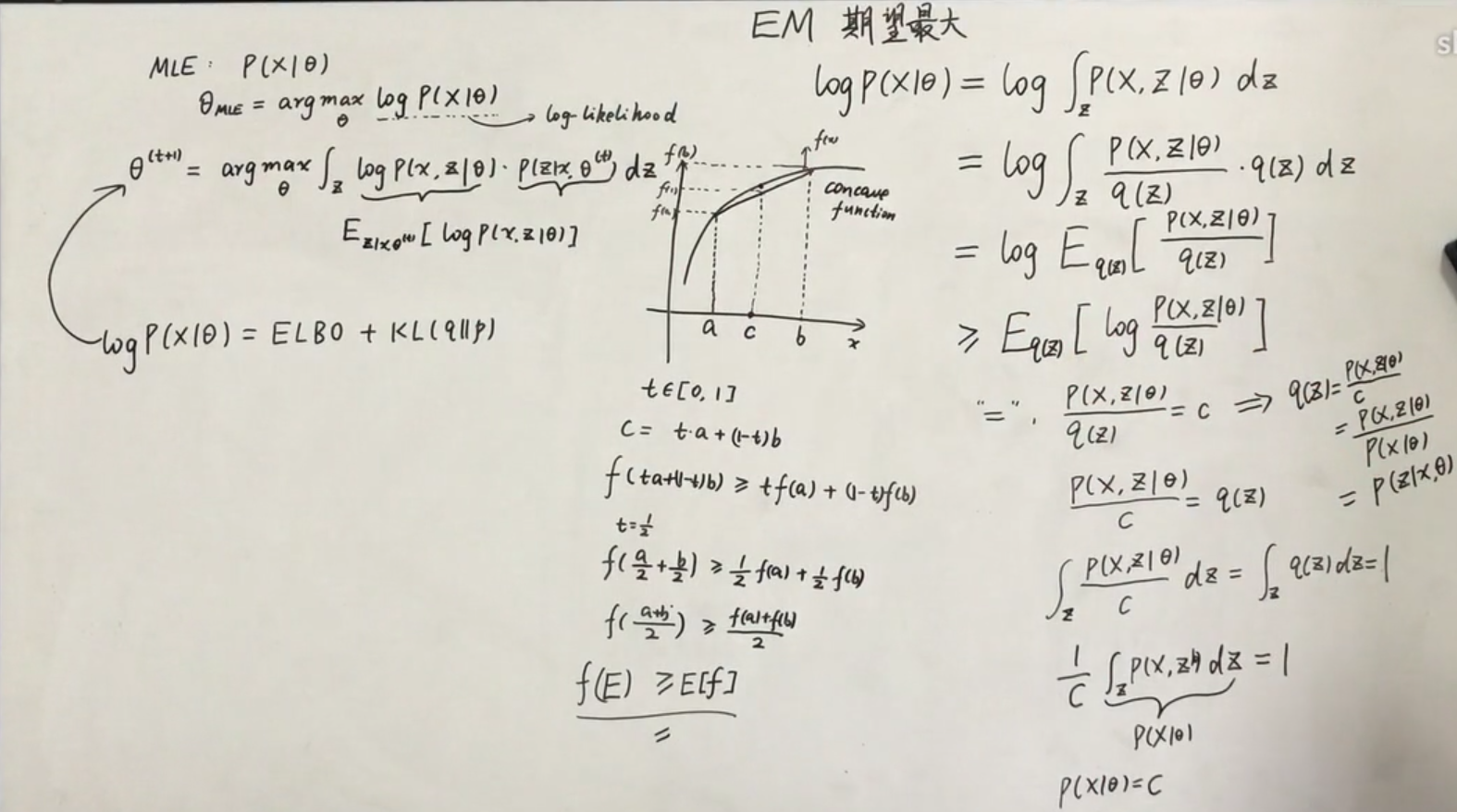
- 核心思想:通过E步骤和M步骤使得期望最大化
- 算法优点:简单稳定
- 算法缺点:迭代速度慢,次数多,容易陷入局部最优;对初始值敏感:EM算法需要初始化参数θ,而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
- 应用领域:参数估计; 计算机视觉的数据集聚; k-means算法是EM算法思想的体现,E步骤为聚类过程,M步骤为更新类簇中心。GMM(高斯混合模型)也是EM算法的一个应用
