Problem 05. longest-palindromic-substring 最长回文子串 枚举方法 动态规划方法 中心扩展方法 马拉车算法
简述
-
最长回文子串问题是一个很经典的问题,也有挺多的解法,且时间复杂度各异。遇到这类题挺多次了, 上学期算法导论课的机考就出现了一道相同的题,当时好像是用动态规划瞎搞就AC了…但后来也没有做总结。。。这里又遇到了这题,肯定不能放过,写一份详细的总结分享给大家,也供自己以后复习用
-
还是先简要介绍一下最长回文子串的概念和定义:最长回文子串问题就是在一个字符串中查找一个最长的连续的回文的子串,例如“banana” 的最长回文子串是“anana”。概念很简单,也很容易理解,解法也很多
-
!!!这里我要提一个很容易踩的坑!!!肯定有不少人(包括我)会提出一个解决办法:
将原字符串 翻转,得到 ,只要找到 和 之间的最长公共子串,那么该子串就是 的最长回文子串
-
这似乎是可行的,例如:
,
它们之间的最长公共子串为 ,恰好是答案 -
但是考虑以下的情况:
,
此时它们之间的最长公共子串为 ,显然他不是回文字符串 -
后面给出我整理的四种解法的具体思路和代码实现
一、枚举
-
最容易想到的方法,就是暴力枚举,思路如下:
-
1)遍历字符串,枚举出所有的子串
-
2)判断每个子串是否为回文子串
-
3)子串为回文串时,判断其是否为当前长度最长的,是的话进行替换和记录;继续进行循环遍历
-
-
时间复杂度分析:
-
遍历字符串枚举子串时,需要两层循环,时间复杂度为
-
而每当枚举出一个子串时,还要判断它是否回文,需要 的时间复杂度,所以总的时间复杂度为
-
-
代码实现:
public static boolean if_palindrome(String s) {
for (int i = 0, j = s.length() - 1; i <=j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
}
return true;
}
public static String longestPalindrome1(String s) {
if (s == null || s.length() <= 1) {
return s;
}
String ans = "";
for (int i = 0; i < s.length(); i++) {
for (int j = i + 1; j < s.length() + 1; j++) {
String tmp = s.substring(i, j);
if (if_palindrome(tmp)) {
if (tmp.length() > ans.length()) {
ans = tmp;
}
}
}
}
return ans;
}
-
测试效果如下,虽然是AC了,但是性能是真滴low

二、动态规划方法
-
“空间换时间”,动态规划的方法能将时间复杂度优化到 ,具体的思路如下:
-
1)回文字符串的以其中心向左右扩展得到的子串也是回文字符串
-
2)比如P[i, j](表示以i开始以j结束的子串)是回文字符串,那么P[i + 1, j - 1]也是回文字符串
-
3)这样的话,最长回文子串问题就能分解成一系列子问题了
-
4)定义状态方程和转移方程如下:
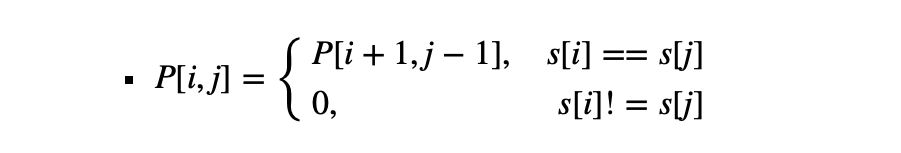
-
5)这样的话就需要额外的 的空间来存储状态,而时间复杂度也为
-
-
代码实现:
public static String longestPalindrome2(String s) {
if (s == null || s.length() <= 1) {
return s;
}
int len = s.length();
boolean[][] dp = new boolean[1000 + 10][1000 + 10];
int start = 0, max_len = 1;
for (int i = 0; i < len; i++) {
dp[i][i] = true;
if (i < len - 1 && s.charAt(i) == s.charAt(i + 1)) {
dp[i][i + 1] = true;
start = i;
max_len = 2;
}
}
for (int tmp = 3; tmp <= len; tmp++) {
for (int i = 0; i <= len - tmp; i++) {
int j = i + tmp - 1;
if (dp[i + 1][j - 1] && s.charAt(i) == s.charAt(j)) {
dp[i][j] = true;
start = i;
max_len = tmp;
}
}
}
return s.substring(start, start + max_len);
}
-
测试效果如下,相对于暴力法大大的优化了

三、中心扩展方法
-
顾名思义,就是取一个中心点,然后左右扩展进行判断,具体思路如下:
-
1)这里要区分回文字符串长度为奇数和偶数的情况
-
2)遍历字符串的每个字符(位置index处的字符)
-
奇数情况:初始low = 初始high = index(low和high控制在原字符串范围内),判断low处和high处的字符是否相等,相等的话low–,high++
-
偶数情况:初始low = index,初始high = index + 1(low和high控制在原字符串范围内),判断low处和high处的字符是否相等,相等的话low–,h
-
-
3)每次low处和high处的字符相同时,都将当前最长回文子串的长度和 进行比较,后者较大时就进行更新操作
-
-
时间复杂度方面,遍历字符串的时候 ,进行左右扩展的时候 ,所以总的时间复杂度为
-
代码实现:
public int expandAroundCenter(String s, int left, int right) {
int l = left, r = right;
while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
return r - l - 1;
}
public String longestPalindrome(String s) {
if (s == null || s.length() <= 1) {
return s;
}
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
-
测试效果如下

四、马拉车算法
- 未总结完。。。待补充。。。