19. 梯度下降

版权声明：转载请注明来源及作者，谢谢！ https://blog.csdn.net/qq_42442369/article/details/86529505

学习梯度下降必备知识

知识准备：导数

汽车在10分钟内行驶3公里。我们可以计算其平均速度，然而，在10分钟内，汽车可能并不总是匀速行驶，因此，如果我们想求汽车在某一时刻的瞬时速度，就可以将时间进行划分成若干段（1分钟，1秒钟等）。随着时间段颗粒度的无限缩短，就能够求解出汽车在某一时刻的瞬时速度了。
导数体现的是某个瞬间的变化量，例如，汽车在某一个时刻的瞬时速度。我们可以将时间（x）与距离（y）表示为函数：
$y = f(x)$
而瞬时速度（导数）则可以体现为在一段时间内，行驶的路程与时间的商：
$f'(x) = \frac{df(x)}{dx} = \lim_{\Delta x \to 0}\frac{f(x + \Delta x) - f(x)}{\Delta x}$
实际上，这就是y的增量与x增量的比值而已（x的微小变化会带来y的多少变化）。在函数图像上，可以表示为曲线的割线，而导数体现为瞬时变化，即当 $\Delta x \to 0$时的变化，这也就是曲线的切线，即曲线的斜率（tan）。

几何上的表现：割线变切线，两个点不断逼近。

知识准备：数值微分原理

数值微分（numerical differentiation），是使用数值方法近似求解函数导数。然而，我们需要注意：

• 在数学上可以表示趋近于0的数，但是在计算机中却不能。
• 我们使用函数求解的是 $x + \Delta x$之间的斜率，而并非函数在 $x$处的斜率（因为第一点原因）。
• 为了减小误差，我们可以计算点 $x$左右两侧的差分（中心差分）。
  
  
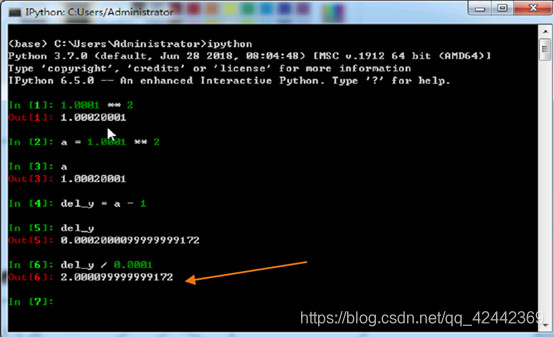
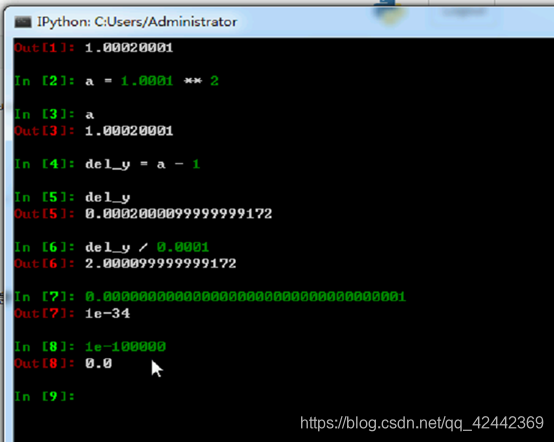
  逼近 y=x^2 2x 导数为2
  数值微分 why不准确；因为数值微分 趋近于0 但毕竟不是0。
  所以数值微分求解 ，数学上 可以表示过，程序上无法表现无限趋近于0。

我们实际要的时割线的斜率
怎么解决
中心的方式表示 除以2倍的，程序如下：

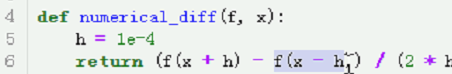
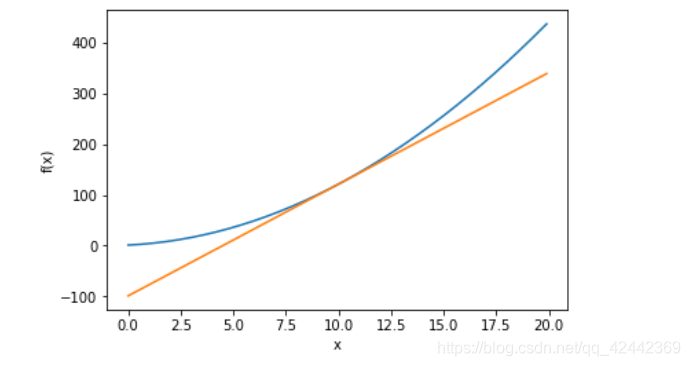
加深理解: 画出导数切线

使用数值微分求解 $y = x ^ 2 + 2x + 1$在x=10点的导数，并画出该点的切线。
$y = f(x)$在点 $(x_0, y_0)$处的切线方程为：
$y - y_0 = f'(x_0)(x - x_0)$

import numpy as np
import matplotlib.pylab as plt

# 使用数值微分求导数值。
# 参数：f 函数
# x 自变量，求哪一点的导数值。
def numerical_diff(f, x):
    # 定义一个很小的增量值。0.0001
    h = 1e-4
    # 使用中心差分求解近似导数值。
    return (f(x + h) - f(x - h)) / (2 * h)

# 定义原函数的方程
def function(x):
    return x ** 2 + 2 * x + 1

# 切线方程
def tangent_line(f, x):
    d = numerical_diff(f, x)
    y = f(x) - d * x
    return lambda t: d * t + y
     
x = np.arange(0.0, 20.0, 0.1)
y = function(x)
plt.xlabel("x")
plt.ylabel("f(x)")

tf = tangent_line(function, 10)
y2 = tf(x)

plt.plot(x, y)
plt.plot(x, y2)
plt.show()

# print(numerical_diff(function, 10))

知识准备：偏导数

当函数具有多个变量时，保持其他变量不变（固定为某个值），而针对其中一个变量求导数，称为偏导数。
对于函数 $f(x_0, x_1, …… x_n)$，对 $x_0$求偏导时，因为其他变量都是固定不变的，因此，可以将其他变量都看成是常数。

设计多个自变量，对那个自变量求偏导，其他的就保持为常数。

梯度概念

梯度是一个向量，表示函数在某一点处的方向导数。
$\bigtriangledown f(x1, x2, ...)=(\frac{\partial f(x1, x2, ...)}{\partial x1}, \frac{\partial f(x1, x2, ...)}{\partial x2}, ...)$
由此可知，当函数是一维函数时，梯度就是导数。

通过梯度求解极值

梯度具有如下的特征：

• 函数在某一点，在该点梯度的方向变化最快。
• 沿着梯度的方向，函数上升最快。
• 逆着梯度的方向，函数下降最快。

因此，我们可以通过梯度指引的方向，进而求解函数的极值。过程为：

扫描二维码关注公众号，回复： 4996529 查看本文章

1. 设定一个初始坐标点。
2. 求解该坐标点的梯度值。
3. 根据梯度值指定的方向，前进一段距离，更新坐标值。
4. 重复步骤2-3，直到迭代到指定的次数，或者连续迭代两次的y值小于指定的阈值为止。

根据求解极值的不同（极大值还是极小值），我们可以分为梯度上升或者梯度下降。在机器学习领域中，梯度下降的应用会更多。

说明：梯度的方向不一定指向极值，但是，沿着梯度的方向更新可以让函数的值朝着极值靠近。

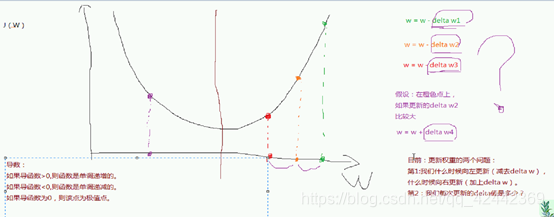
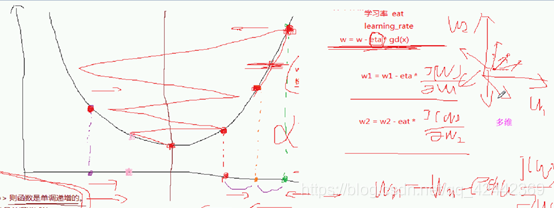
一维梯度下降

程序：使用梯度下降求解方程 $y=x^{2} - 2x + 1$的最小值。
观察学习率对梯度下降的影响。学习率不是越大越好，也不是越小越好。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"]=False

# 定义原函数方程。
def f(x):
    return x ** 2 - 2 * x + 1

# 定义梯度方程（导函数方程）
def gradient(x):
    return 2 * x - 2

# 定义初始值，即梯度下降最开始的迭代点。
x = 10
# 保存每次调整后，x的值以及x所对应的y值。即调整过程中，x与y的移动轨迹。
x_list = []
y_list = []
# 定义学习率（每次进行调整的幅度系数）
# 关于学习率的设置：学习率要设置得当，既不是越大越好，也不是越小越好。
# 如果学习率设置过小，则每次更新的非常缓慢，需要迭代很多次才能到极值附近。
# 如果学习率设置过大，则会出现震荡发散的情况，导致跳过最优解。
eta = 1.5

# 进行迭代
for i in range(30):
    # 将每次调整的值加入到列表中。
    x_list.append(x)
    y_list.append(f(x))
    # 根据梯度值来调整x，使得调整的x，能够令f(x)的值更小。
    x -= eta * gradient(x)
# 输出更新的值（更新的轨迹）
print(y_list)
print(x_list)

%matplotlib qt
x = np.linspace(-9, 11, 200)
y = x ** 2 - 2 * x + 1
plt.plot(x, y)
# title中也支持Latex公式。
plt.title("函数$y=x^{2}-2x+1$的图像")
plt.plot(x_list, y_list, "ro--")
plt.show()

二维梯度下降

程序：使用梯度下降求解方程 $y = 0.2(x1 + x2) ^ {2} - 0.3x1x2 + 0.4$的最小值。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib qt

mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"]=False

# 定义原函数
def f(x1, x2):
    return 0.2 * (x1 + x2) ** 2 - 0.3 * x1 * x2 + 0.4

# 针对x1求梯度值。
def gradient_x1(x1, x2):
    return 0.4 * (x1 + x2) - 0.3 * x2

# 针对x2求梯度值。
def gradient_x2(x1, x2):
    return 0.4 * (x1 + x2) - 0.3 * x1

# 定义学习率
alpha = 0.5
# 定义列表，存放x1，x2与y的移动轨迹。
x1_list = []
x2_list = []
y_list = []

# 定义初始点。
x1, x2 = 4.8, 4.5

for i in range(50):
    # 使用列表加入x1，x2，与y的轨迹信息。
    x1_list.append(x1)
    x2_list.append(x2)
    y_list.append(f(x1, x2))
    # 根据梯度值调整每个自变量。
    x1 -= alpha * gradient_x1(x1, x2)
    x2 -= alpha * gradient_x2(x1, x2)

print(x1_list)
print(x2_list)
print(y_list)

![在这里插入图片描述](https://img-blog.csdnimg.cn/20190117165301915.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQyNDQyMzY5,size_16,color_FFFFFF,t_70)

X1 = np.arange(-5, 5, 0.1)
X2 = np.arange(-5, 5, 0.1)
X1, X2 = np.meshgrid(X1, X2)
Y = np.array([X1.ravel(), X2.ravel()]).T
Y = f(Y[:, 0], Y[:, 1])
Y = Y.reshape(X1.shape)

fig = plt.figure()
ax = Axes3D(fig)
# 绘制方程曲面。
surf = ax.plot_surface(X1, X2, Y, rstride=5, cstride=5, cmap="rainbow")
# 绘制x1,x2,y的移动轨迹。
ax.plot(x1_list, x2_list, y_list, 'bo--')
# 指定为哪一个图形生成颜色条。
fig.colorbar(surf)
plt.title("函数$y = 0.2(x1 + x2) ^ {2} - 0.3x1x2 + 0.4$")
plt.show()

plt.scatter(x1_list, x2_list, c="r")

# m = plt.contourf(X1, X2, Y, 10)
# 画出等高线。
# 第4个参数（level）：用来指定等高线的数量与位置。
# 直观的讲，该值越大，则等高线越密，否则越稀疏。
# m = plt.contour(X1, X2, Y, 25)

# 绘制填充的等高线。
m = plt.contourf(X1, X2, Y, 15)
# 在等高线上绘制x1与x2的移动轨迹。
plt.scatter(x1_list, x2_list, c="r")
plt.colorbar(m)

更新

对于损失函数：
$J(w) = \frac{1}{2}\sum_{i=1}^{m}(y ^ {(i)} - w ^ {T}x ^ {(i)}) ^ {2}$
我们可以使用梯度下降的方式，不断去调整权重w，进而去减小损失函数J(w)的值。经过不断迭代，最终求得最优的权重w，使得损失函数的值最小（近似最小）。
调整方式为：
$w_j = w_j - \eta\frac{\partial J(w)}{\partial w_j}$
我们这里先单独对一个样本求梯度来演示，所有样本，只需要分别对每个式子进行求梯度，最后将每个求梯度的结果求和即可。

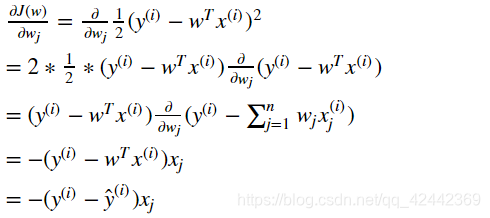
不断调整w

按照每个分量的偏量方向 调整
对每个自变量求偏导

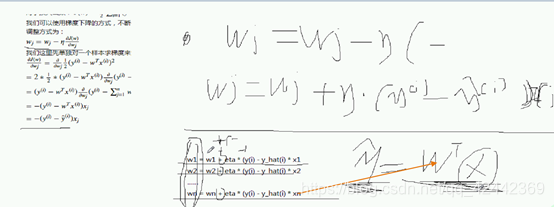
梯度下降能求解，能作用于损失函数

梯度 向量 分量 取值 每个函数取偏导
认为是向量

梯度的特征：3点

特度更重要的记住：梯度是方向导数
取梯度的时候，梯度值
更重要的是 梯度值>0 则原函数是单调递增

找到w使得jw损失函数最小
梯度下降 求线性回归也是可以的
使用梯度下降求梯度下降

梯度值 凸函数 有 极小值
梯度下降的精髓：

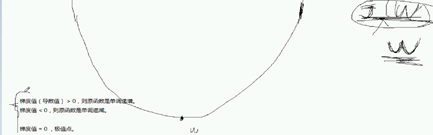
数学里面不管，只管
上升和下降没怎么关

通常情况下梦不到
但是我们可以取调整

最开始给定的w是这个

我们可以往左调 可以往有调
取决于 梯度值 》0 <0 不看等于0 等于0就是季度之
一般是到不了极值点 越接近 越换

一维的时候 左右？

二维，有w1 w2 w1 有左右 w2上下

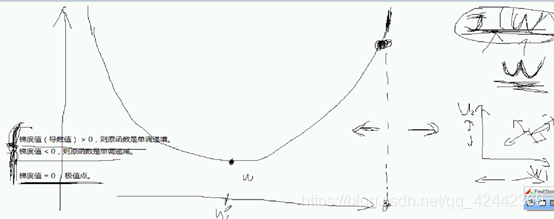
调整左还是右呢？
大于0 单调递增 w越大 梯度越大 我们得然他减小
应该往左

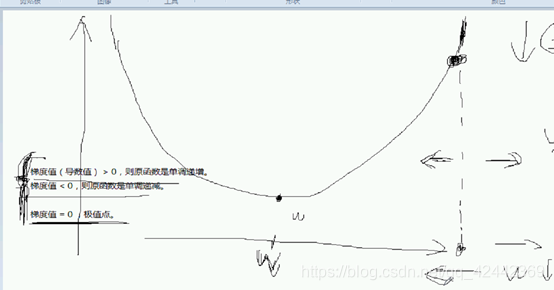
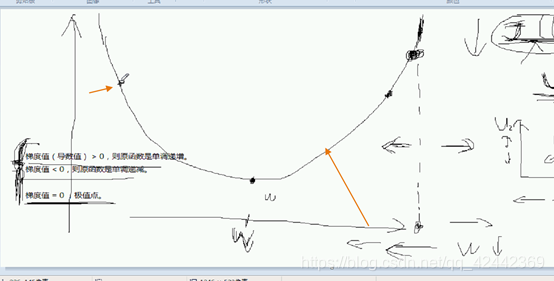
右边 > 0 继续减
左边 <0 w增大 让它往右

如此迭代反复，我们就能让它接近极值点

和我们增加最快，减小最快，其实一点关系都没有！！！

因为梯度的方向很可能并不能指向极值点，但是我们移动的时候靠近极值点

不是一条直线 梯度值都一样

因为我们只能保证这一点的梯度，所以跟上升最快下降最快一点关系没有

所以梯度 只是控制方向，梯度大小，只是跟学习率有关
我们可以卖一步很小 卖一步很大
Delta w取多少？

我们就以梯度为移动不服，不是为了快，而是为了方便

所以我们有eta系数

取决于梯度值 大于0 还是小于0
梯度值》0 我们
梯度值<0

所以deltaw沃恩应该是让它增加还是减小了呢？
所以我们用w的性质

根据w来的
所以我们可以用求偏导数来控制

0 减一个w

上面就是这个式子

所以梯度不是不符
梯度只是控制方向

不符和大小由eta控制

最后更新的式子

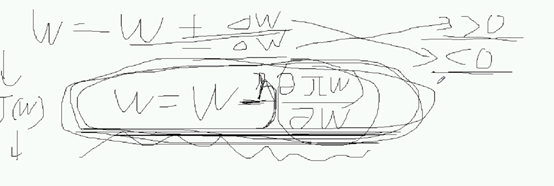
然后是程序的实例：

一维的

二维的

关于eta值，不易于过大，就越过了极值点

如果是多维的，就对每一个维度进行更新
更新x1的时候就对x1求偏导
X2 就是 x2求偏导

数据的维度，是和数组的维度一样吗？

嵌套的层数，数组的

数据集的维度，特征的数量，就是多少列，多少个维度，why?

Eg.人员

年龄，身高，体重，
三列，三个周，三个维度

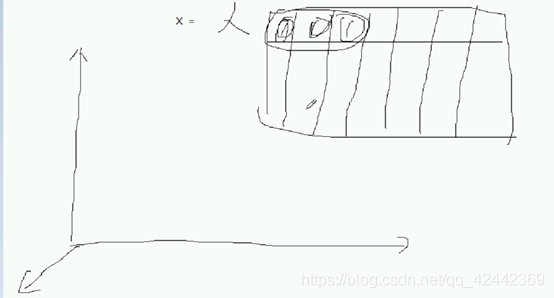
一个坐标轴就是一个维度

可视化画图

画等高线 新学的
X1 x2 取不同值的时候，能让y相等

最后说了下

损失函数不同，难道每个w写一个梯度函数吗？

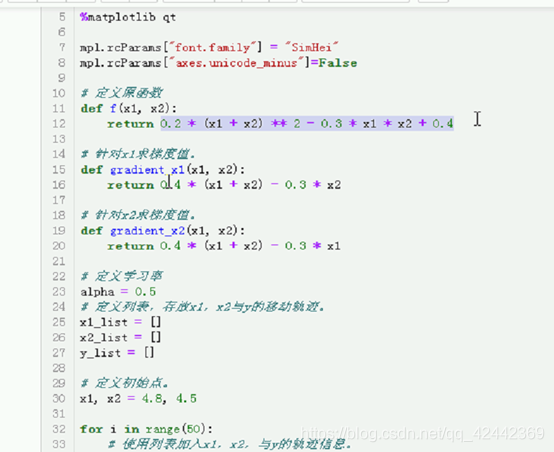
从通用角度来看，能不能有通用形式？对蓝求偏导

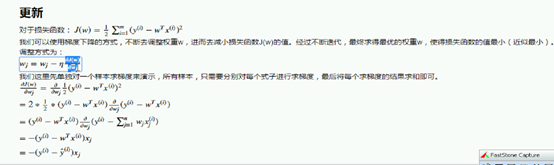
拆开 对 a+b 求导

标签求导0 后面一部分
对里面的一项 wj 求偏导 其他都是常数 0

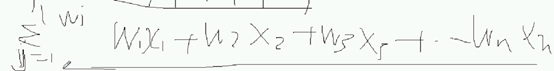
最后的结果是xj

所以对w更新 有一个通用的公式

然后利用它不断迭代 能够求出来

生成数据集

然后拆分，拆不拆其实无所谓
还是拆一下

这是线性回归的结果：

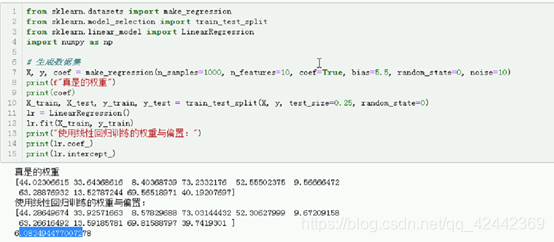
然后我们用梯度下降解一下

SGD随机梯度下降
学习率 给定迭代次数 模仿下面的

放到相关的对象中

也定义一个方法
Wb

不可能是构造器里进行初始化的，都是fit学出来的，所以后面加上
就是命名惯例

初始化的构造器里面指定的就是超参数

就能知道参数到底是学习出来的还是指定出来的

对于每一个样本用这个公式

循环一次拿出值

平行遍历多个可迭代对象 用zip





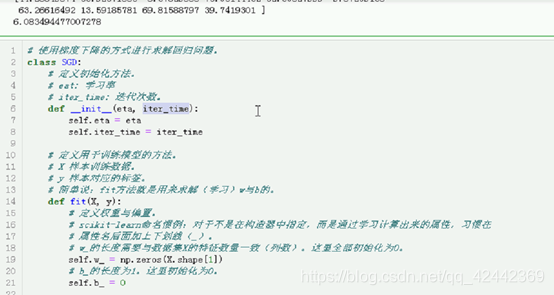
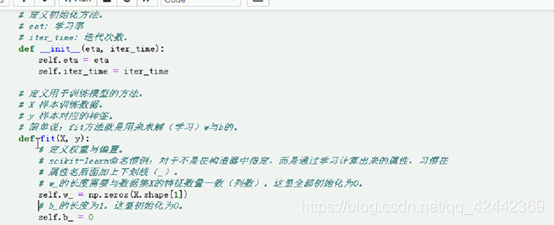
套入公式后不断迭代

超参数 eta 慎重 给0.01 itertime 100
Diaoyong fit方法 xtrain ytrina 传进去

进行迭代一轮 一共迭代itertime轮

如果50轮达到很好的效果，就不用

加上self

训练完周后 w He b就像有了

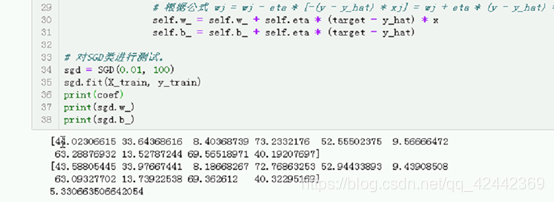
梯度下降的方式也很不错

那么给我们一个未知的p就能预知

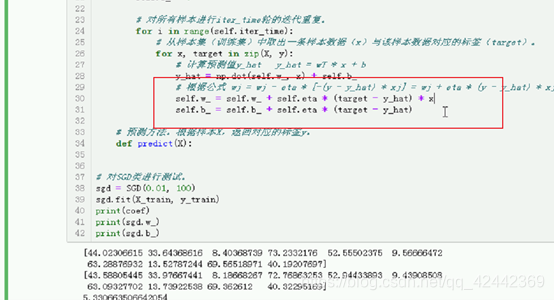
W跟新的时候没用循环 采用的时矢量化计算

现在可以预测了

预测的第一个样本的第一个特征

N个特征 m个样本

第m个样本的第n个特征，这就是带特征的预测集
一会儿传测试集

常规方式的话 每次用循环 一次提一个小样本

广播之后 矢量化计算


一次 对位相乘 再相加
最后的 yhat 。。
一下子 预测值都得出
所以我们就可以利用numpy的矩阵方法 dot方法，不用循环

多维和一维 w 和 b

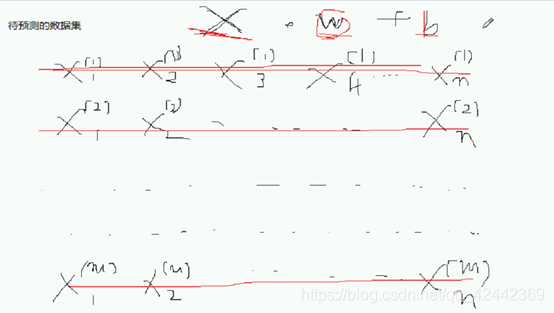
解决方法 点乘+b就搞定了

模型最难的时fit fit学习参数

这个结果

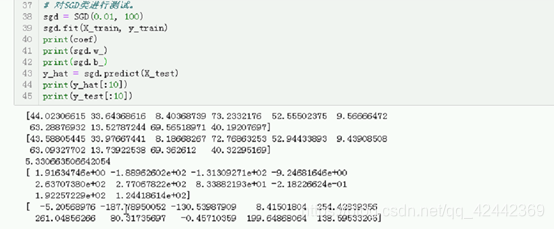
还是差不多 有的用e表示 这就his预测表示的结果

别只记得score 还有

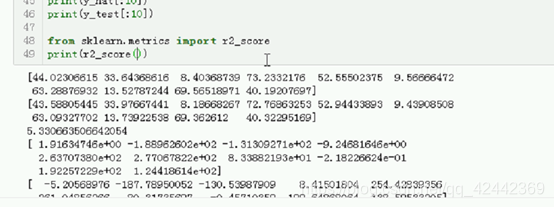
值传进来

把 ytrue ypredict穿过来 0.99 高 因为 noise小

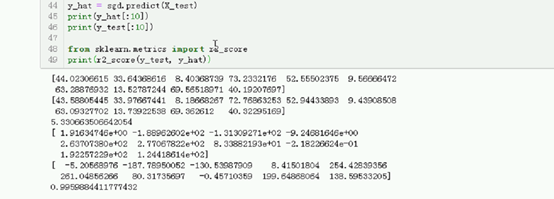
最关键的 是用梯度下降进行更新

注意

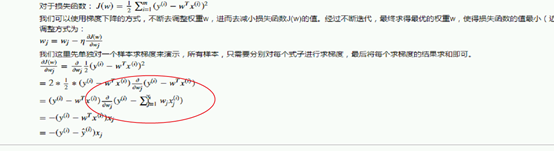
这一个快 对 w0 求骗到 w0 * 1

更新b前面乘以1 等于没成

根据方式求梯度下降 求 wj 最后得到比较理想的结果

梯度下降非常有意义，因为后面的梯度下降就靠这个算法
梯度下降球迷 最好的解决放啊发

之前学的就是随机梯度下降

现在使用的时批量梯度下降

批量梯度下降的更新方式：
不同之处在于：样本集汇中具有m个样本

随机梯度下降 M个样本会更新m次 速度快
只会更新wj 因为要进行累计求和 再

训练集100轮迭代

100Epoch 100个epoch

随机梯度下降 SGD 会进行多少次更新？

SGD
BGD

一轮只更新一次
求和进行更新

对于批量梯度下降 一轮不管有多少个
100轮 更新100次
样本集大的，耗内存多

有差异性，带表损失函数不一致

一个样本一个样本更新，带有误差，噪声大 异常样本
样本和样本之间，更新的方向也会有影响

随机梯度下降，更新的方向会语无伦次

尽管是向着极值点进行起那就，但是多轮次

最后再极值点附近进行徘徊，因为每一个样本每一个样本更新

就会比较稳定

所以SGD BSD对比
评率快快 但是 波折性
Bsd 跟新慢 但更新起来基本会朝着稳定的方向

因为SGD根据每个样本嘛

SGD可能跳过局部最优点 凸函数 因为是晃荡的


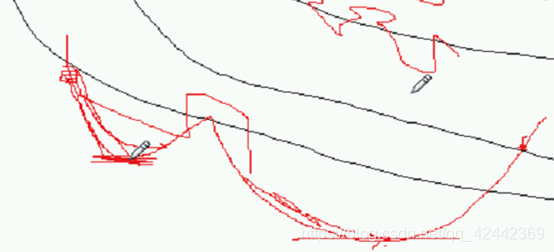
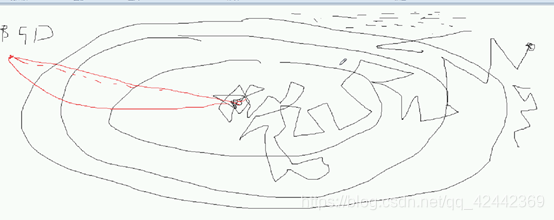
能不能在SGD 和 BGD之间找到结合的？

小批量梯度下降 MBGD

M个样本
一次取k
0<=k<=m

小批量梯度下降
K=1 累加没了 就是随机
K=m 就是批量梯度下降

之前是手写梯度下降，但是主要是让大家明白原理，对线性回归也是促进作用

那我们看skleran中的

SGRegressor
一点一点来 慢慢来
Eta0 初始 随着迭代次数一点一点减少 学习率的衰减


Max iter指定，不指定警告

练习

：使用梯度下降求解之前的线性回归问题。

X, y, coef = make_regression(n_samples=1000, n_features=10, coef=True, bias=5.5, random_state=0, noise=10)

提示：
定义一个数组w，含有元素的数量与生成的特征数量一致。
定义一个偏置b。

梯度下降，需要自变量具有一个初始值，这里可以将w与b全部设置为初始值0，或者很小的数值。
自定义一个合适的学习了eta值。

再来一层循环【定义对所有的样本迭代的次数】
对X与y进行遍历，每次取出一个样本的数据（x）与对应的标签（target）【循环】
y_hat = w与每一个样本数据x进行对位相乘再相加， 再加上b。
w = w + eta * (y - y_hat)
再说一下 标准化处理




## 练习：使用梯度下降求解之前的线性回归问题。
X, y, coef = make_regression(n_samples=1000, n_features=10, coef=True, bias=5.5, random_state=0, noise=10)

提示：
定义一个数组w，含有元素的数量与生成的特征数量一致。
定义一个偏置b。

梯度下降，需要自变量具有一个初始值，这里可以将w与b全部设置为初始值0，或者很小的数值。
自定义一个合适的学习了eta值。

再来一层循环【定义对所有的样本迭代的次数】
对X与y进行遍历，每次取出一个样本的数据（x）与对应的标签（target）【循环】
y_hat = w与每一个样本数据x进行对位相乘再相加， 再加上b。
w = w + eta * (y - y_hat)

程序解释

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import numpy as np

# 生成数据集
X, y, coef = make_regression(n_samples=1000, n_features=10, coef=True, bias=5.5, random_state=0, noise=10)
print(f"真是的权重")
print(coef)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
lr = LinearRegression()
lr.fit(X_train, y_train)
print("使用线性回归训练的权重与偏置：")
print(lr.coef_)
print(lr.intercept_)

# 使用梯度下降的方式进行求解回归问题。
class SGD:
    # 定义初始化方法。
    # eat: 学习率
    # iter_time: 迭代次数。
    def __init__(self, eta, iter_time):
        self.eta = eta
        self.iter_time = iter_time
    
    # 定义用于训练模型的方法。
    # X 样本训练数据。
    # y 样本对应的标签。
    # 简单说：fit方法就是用来求解（学习）w与b的。
    def fit(self, X, y):
        # 定义权重与偏置。
        # scikit-learn命名惯例：对于不是在构造器中指定，而是通过学习计算出来的属性，习惯在
        # 属性名后面加上下划线（_）。
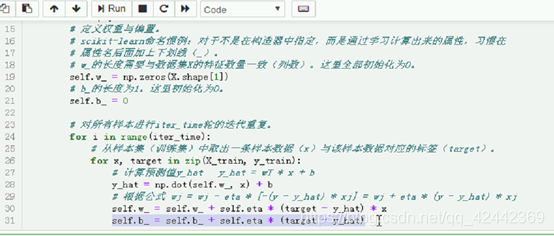
        # w_的长度需要与数据集X的特征数量一致（列数）。这里全部初始化为0。
        self.w_ = np.zeros(X.shape[1])
        # b_的长度为1。这里初始化为0。
        self.b_ = 0
        
        # 对所有样本进行iter_time轮的迭代重复。
        for i in range(self.iter_time):
            # 从样本集（训练集）中取出一条样本数据（x）与该样本数据对应的标签（target）。
            for x, target in zip(X, y):
                # 计算预测值y_hat   y_hat = wT * x + b
                y_hat = np.dot(self.w_, x) + self.b_
                # 根据公式 wj = wj - eta * [-(y - y_hat) * xj] = wj + eta * (y - y_hat) * xj
                self.w_ = self.w_ + self.eta * (target - y_hat) * x
                self.b_ = self.b_ + self.eta * (target - y_hat)
           
    # 预测方法。根据样本X，返回对应的标签y。
    def predict(self, X):
        return np.dot(X, self.w_) + self.b_
    
#     def socre()
    
    
# 对SGD类进行测试。
sgd = SGD(0.01, 100)
sgd.fit(X_train, y_train)
print(coef)
print(sgd.w_)
print(sgd.b_)
y_hat = sgd.predict(X_test)
print(y_hat[:10])
print(y_test[:10])

from sklearn.metrics import r2_score
print(r2_score(y_test, y_hat))

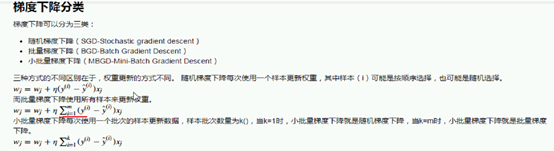
梯度下降分类

梯度下降可以分为三类：

• 随机梯度下降（SGD-Stochastic gradient descent）
• 批量梯度下降（BGD-Batch Gradient Descent）
• 小批量梯度下降（MBGD-Mini-Batch Gradient Descent）

三种方式的不同区别在于，权重更新的方式不同。
随机梯度下降每次使用一个样本更新权重，其中样本（i）可能是按顺序选择，也可能是随机选择。
$w_j = w_j + \eta(y ^ {(i)} - \hat y ^ {(i)})x_j$
而批量梯度下降使用所有样本来更新权重。
$w_j = w_j + \eta\sum_{i=1}^{m}(y ^ {(i)} - \hat y ^ {(i)})x_j$
小批量梯度下降每次使用一个批次的样本更新数据，样本批次数量为k()，当k=1时，小批量梯度下降就是随机梯度下降，当k=m时，小批量梯度下降就是批量梯度下降。
$w_j = w_j + \eta\sum_{i=1}^{k}(y ^ {(i)} - \hat y ^ {(i)})x_j$

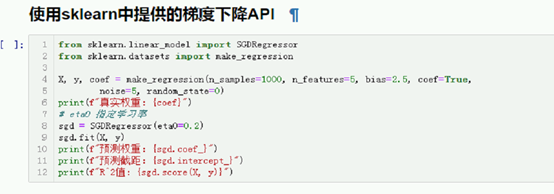
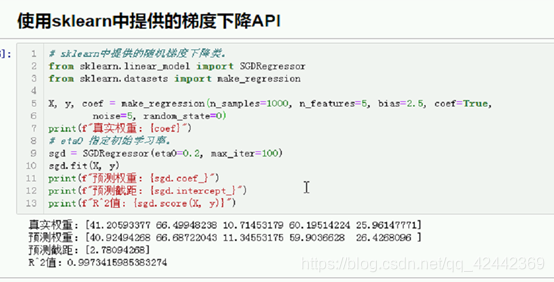
使用sklearn中提供的梯度下降API

# sklearn中提供的随机梯度下降类。
from sklearn.linear_model import SGDRegressor
from sklearn.datasets import make_regression

X, y, coef = make_regression(n_samples=1000, n_features=5, bias=2.5, coef=True,
        noise=5, random_state=0)
print(f"真实权重：{coef}")
# eta0 指定初始学习率。
sgd = SGDRegressor(eta0=0.2, max_iter=100)
sgd.fit(X, y)
print(f"预测权重：{sgd.coef_}")
print(f"预测截距：{sgd.intercept_}")
print(f"R^2值：{sgd.score(X, y)}")

深入浅出–梯度下降法及其实现（转载）

转自：https://www.jianshu.com/p/c7e642877b0e
作者：六尺帐篷

• 梯度下降的场景假设
• 梯度
• 梯度下降算法的数学解释
• 梯度下降算法的实例
• 梯度下降算法的实现
• Further reading

本文将从一个下山的场景开始，先提出梯度下降算法的基本思想，进而从数学上解释梯度下降算法的原理，最后实现一个简单的梯度下降算法的实例！

梯度下降的场景假设

梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的，而是需要一个复杂的工具来测量，同时，这个人此时正好拥有测量出最陡峭方向的能力。所以，此人每走一段距离，都需要一段时间来测量所在位置最陡峭的方向，这是比较耗时的。那么为了在太阳下山之前到达山底，就要尽可能的减少测量方向的次数。这是一个两难的选择，如果测量的频繁，可以保证下山的方向是绝对正确的，但又非常耗时，如果测量的过少，又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率，来确保下山的方向不错误，同时又不至于耗时太多！

梯度下降

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢？接下来，我们从微分开始讲起

微分

看待微分的意义，可以有不同的角度，最常用的两种是：

函数图像中，某点的切线的斜率

函数的变化率
几个微分的例子：

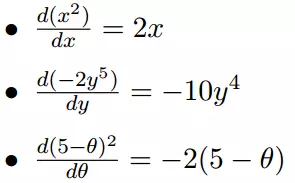
上面的例子都是单变量的微分，当一个函数有多个变量的时候，就有了多变量的微分，即分别对每个变量进行求微分

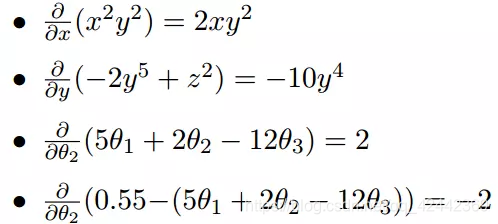
梯度

梯度实际上就是多变量微分的一般化。
下面这个例子：

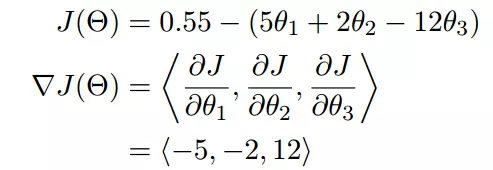
我们可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>包括起来，说明梯度其实一个向量。
梯度是微积分中一个很重要的概念，之前提到过梯度的意义

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！

梯度下降算法的数学解释

上面我们花了大量的篇幅介绍梯度下降算法的基本思想和场景假设，以及梯度的概念和思想。下面我们就开始从数学上解释梯度下降算法的计算过程和思想！

此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点！

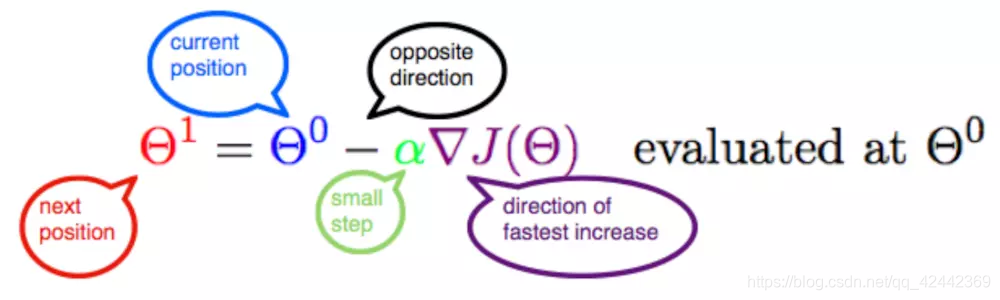
下面就这个公式的几个常见的疑问：

α是什么含义？
α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大扯着蛋，哈哈，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

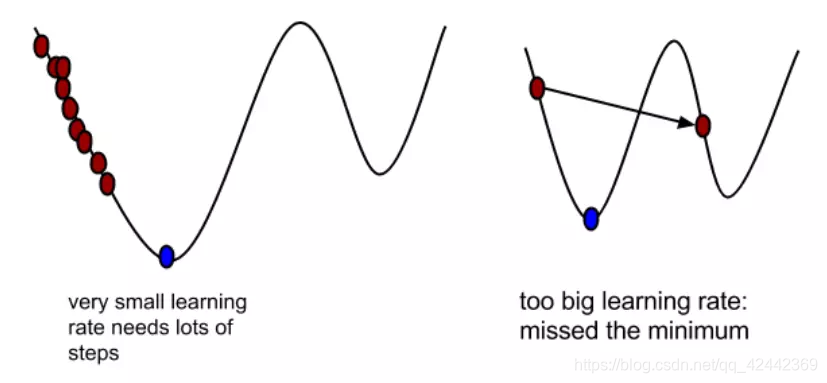
为什么要梯度要乘以一个负号？
梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号

梯度下降算法的实例

我们已经基本了解了梯度下降算法的计算过程，那么我们就来看几个梯度下降算法的小实例，首先从单变量的函数开始

单变量函数的梯度下降

我们假设有一个单变量的函数

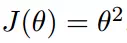
函数的微分

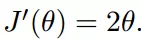
初始化，起点为

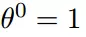
学习率为

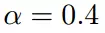
根据梯度下降的计算公式

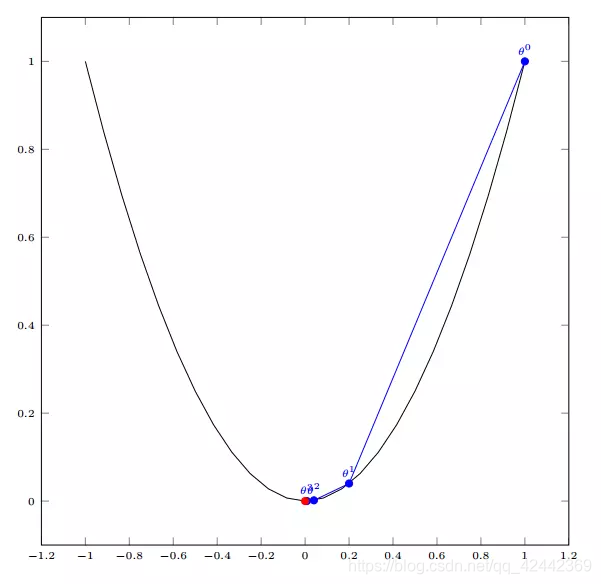
我们开始进行梯度下降的迭代计算过程：

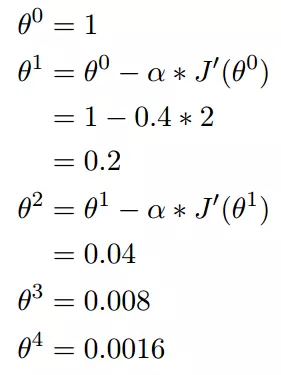
如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底

多变量函数的梯度下降

我们假设有一个目标函数

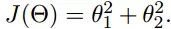
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0，0)点。但是接下来，我们会从梯度下降算法开始一步步计算到这个最小值！
我们假设初始的起点为：

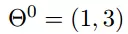
初始的学习率为：

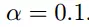
函数的梯度为：

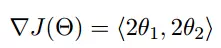
进行多次迭代：

我们发现，已经基本靠近函数的最小值点

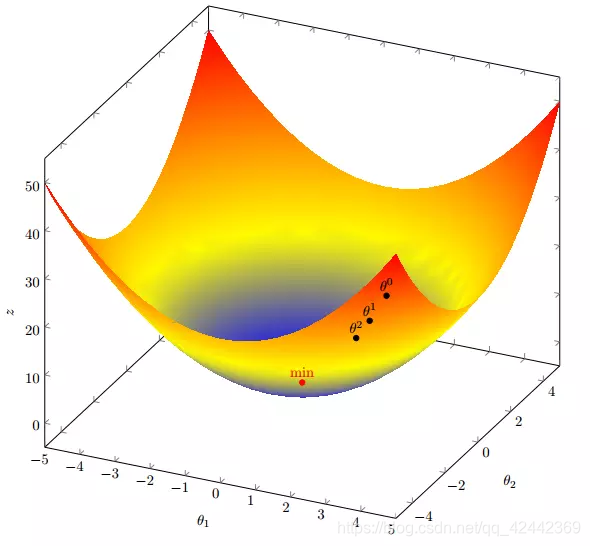
梯度下降算法的实现

下面我们将用python实现一个简单的梯度下降算法。场景是一个简单的线性回归的例子：假设现在我们有一系列的点，如下图所示

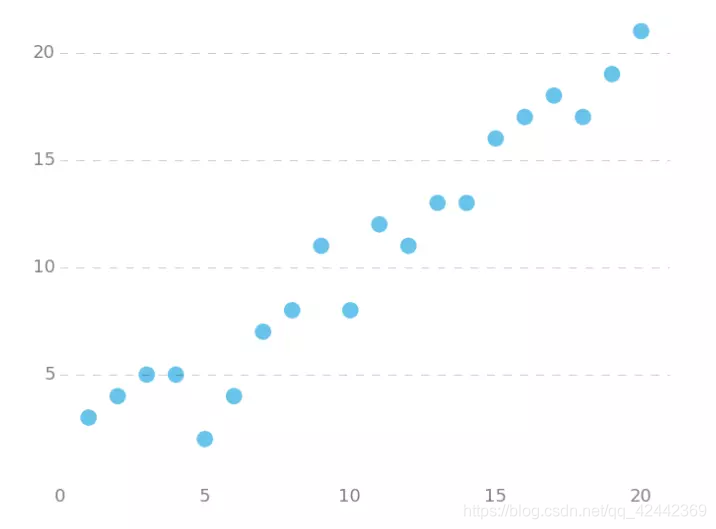
我们将用梯度下降法来拟合出这条直线！

首先，我们需要定义一个代价函数，在此我们选用均方误差代价函数

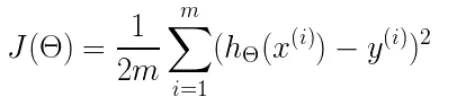
此公式中

m是数据集中点的个数
½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
y 是数据集中每个点的真实y坐标的值

h 是我们的预测函数，根据每一个输入x，根据Θ 计算得到预测的y值，即

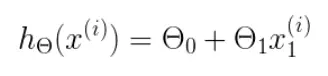
我们可以根据代价函数看到，代价函数中的变量有两个，所以是一个多变量的梯度下降问题，求解出代价函数的梯度，也就是分别对两个变量进行微分

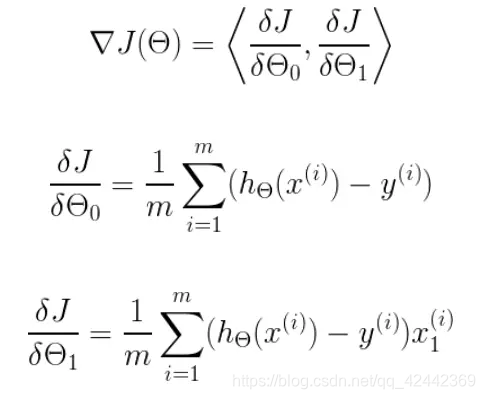
明确了代价函数和梯度，以及预测的函数形式。我们就可以开始编写代码了。但在这之前，需要说明一点，就是为了方便代码的编写，我们会将所有的公式都转换为矩阵的形式，python中计算矩阵是非常方便的，同时代码也会变得非常的简洁。

为了转换为矩阵的计算，我们观察到预测函数的形式

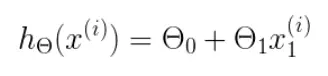
我们有两个变量，为了对这个公式进行矩阵化，我们可以给每一个点x增加一维，这一维的值固定为1，这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算

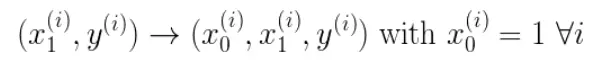
然后我们将代价函数和梯度转化为矩阵向量相乘的形式

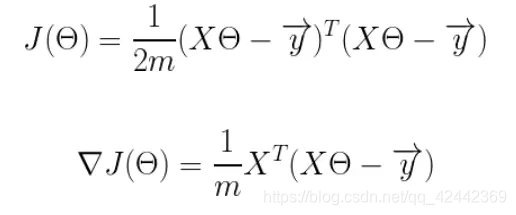
coding

首先，我们需要定义数据集和学习率

import numpy as np

# Size of the points dataset.
m = 20

# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))

# Points y-coordinate
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)

# The Learning Rate alpha.
alpha = 0.01

接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度

def error_function(theta, X, y):
    '''Error function J definition.'''
    diff = np.dot(X, theta) - y
    return (1./2*m) * np.dot(np.transpose(diff), diff)

def gradient_function(theta, X, y):
    '''Gradient of the function J definition.'''
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)

作者：六尺帐篷
链接：https://www.jianshu.com/p/c7e642877b0e
來源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。

最后就是算法的核心部分，梯度下降迭代计算

def gradient_descent(X, y, alpha):
    '''Perform gradient descent.'''
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
    return theta

当梯度小于1e-5时，说明已经进入了比较平滑的状态，类似于山谷的状态，这时候再继续迭代效果也不大了，所以这个时候可以退出循环！

完整的代码如下

import numpy as np

# Size of the points dataset.
m = 20

# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))

# Points y-coordinate
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)

# The Learning Rate alpha.
alpha = 0.01

def error_function(theta, X, y):
    '''Error function J definition.'''
    diff = np.dot(X, theta) - y
    return (1./2*m) * np.dot(np.transpose(diff), diff)

def gradient_function(theta, X, y):
    '''Gradient of the function J definition.'''
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)

def gradient_descent(X, y, alpha):
    '''Perform gradient descent.'''
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
    return theta

optimal = gradient_descent(X, y, alpha)
print('optimal:', optimal)
print('error function:', error_function(optimal, X, y)[0,0])

运行代码，计算得到的结果如下

所拟合出的直线如下

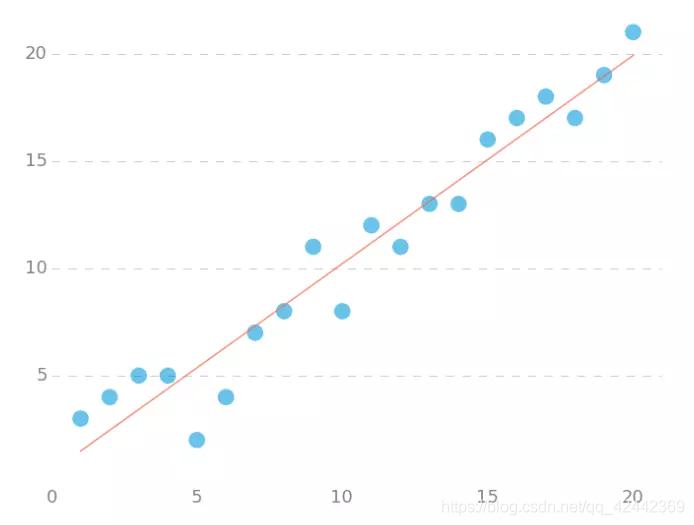
小结
至此，我们就基本介绍完了梯度下降法的基本思想和算法流程，并且用python实现了一个简单的梯度下降算法拟合直线的案例！
最后，我们回到文章开头所提出的场景假设:
这个下山的人实际上就代表了反向传播算法，下山的路径其实就代表着算法中一直在寻找的参数Θ，山上当前点的最陡峭的方向实际上就是代价函数在这一点的梯度方向，场景中观测最陡峭方向所用的工具就是微分 。在下一次观测之前的时间就是有我们算法中的学习率α所定义的。
可以看到场景假设和梯度下降算法很好的完成了对应！
Further reading

Gradient Descent lecture notes from UD262 Udacity Georgia Tech ML Course.

An overview of gradient descent optimization algorithms.