FFT快速傅里叶变换 — 从入门到入坟

其他 2019-01-19 18:07:23 阅读次数: 0
版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/niiick/article/details/85378959

引言

F F T ( F a s t   F o u r i e r   T r a n s f o r m a t i o n ) FFT (Fast\ Fourier\ Transformation) 快速傅里叶变换

不少 O I e r OIer 应该都曾听过 FFT (Fuck Fuck TLE) 这样一个神(gui)奇(chu)算法
不得不说数论蒟蒻在看它证明的时候脑袋里只有三个想法
“我是谁？” “我在哪？” “我在干嘛？”

但认真学完又不得不赞叹数论的奇妙啊
各种鬼畜证明后代码只用简洁的10行就让多项式乘法达到 O ( n l o g n ) O(nlogn) 复杂度

所以我们下面就来看看FFT的优(gui)美(chu)证明吧
F B I    W a r n i n g FBI\ \ Warning 大量数论定理及证明即将来袭，请在dalao陪同下食用

多项式的系数表达

多项式的系数表达应该是在日常运算中较常用的一种表示法

即对于一个次数界为 n n 的多项式 A ( x ) A(x)
其可以表示为这样的形式 A ( x ) = ∑ i = 0 n − 1 a i ∗ x i A(x)=\sum_{i=0}^{n-1}a_i*x^i
那么多项式 A ( x ) A(x) 的系数所组成的向量 a ⃗ = ( a 0 , a 1 , . . . a n − 1 ) \vec{a}=(a_0,a_1,...a_{n−1}) 是这个多项式的系数表达

基于系数表达的多项式，对于一个给定的值 x = x 0 x=x_0
显然我们可以利用秦九韶算法 O ( n ) O(n) 计算 A ( x 0 ) A(x_0)

多项式的点值表达

点值表示可能对大多接触数论较少的人是个不熟悉的名词

一个次数界为 n n 的多项式 A ( x ) A(x) 的点值表达为一个由 n n 个点值对所组成的集合:
{ ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n − 1 , y n − 1 ) } \{(x_0,y_0),(x_1,y_1),(x_2,y_2),...,(x_{n−1},y_{n−1})\}
满足所有的 x k ( 0 ≤ k ≤ n − 1 ) x_k(0\leq k \leq n-1) 各不相同

- 插值多项式唯一性定理

定理：对于任意 n n 个点值对所组成的集合 { ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n − 1 , y n − 1 ) } \{(x_0,y_0),(x_1,y_1),(x_2,y_2),...,(x_{n−1},y_{n−1})\} ，若其中所有 x k x_k 不同
则存在唯一的次数界为 n n 的多项式 A ( x ) A(x) ，满足 y k = A ( x k ) ( 0 ≤ k ≤ n − 1 ) y_k=A(x_k)(0\leq k \leq n-1)

证明：
可以考虑借助增广矩阵作个简单证明
[ a 0 a 1 a 2 . . . a n − 1 ] ∗ [ 1 x 0 x 0 2 . . . x 0 n 1 x 1 x 1 2 . . . x 1 n 1 x 2 x 2 2 . . . x 2 n . . . . . . . . . . . . . . . 1 x n − 1 x n − 1 2 . . . x n n ] = [ y 0 y 1 y 2 . . . y n − 1 ] \left[ \begin{matrix} a_0 \\ a_1 \\ a_2 \\ ... \\ a_{n-1} \end{matrix} \right]*\left[ \begin{matrix} 1 & x_0 & x_0^2 & ... & x_0^n\\ 1 & x_1 & x_1^2 & ... & x_1^n\\ 1 & x_2 & x_2^2 & ... & x_2^n \\ ... & ... & ... &... & ...\\ 1 & x_{n-1} & x_{n-1}^2&...&x_n^n \end{matrix} \right]=\left[ \begin{matrix} y_0 \\ y_1 \\ y_2 \\ ... \\ y_{n-1} \end{matrix} \right]
中间的那一大坨就是范德蒙德矩阵，记为 V ( x 0 , x 1 , . . . , x n − 1 ) V(x_0,x_1,...,x_{n−1})
它的行列式计算公式为 d e t ( V ) = ∏ 0 ≤ j < k ≤ n ( x k − x j ) det(V)=\prod_{0\leq j <k\leq n}(x_k-x_j)
因为 x x 两两不同，所以一定有 d e t ( V ) ! = 0 det(V)!=0 ，即证明该矩阵可逆
因此给定点值表达 y ⃗ \vec{y} ，则能确定唯一的系数表达 a ⃗ \vec{a} ，使得 a ⃗ = V − 1 ( x 0 , x 1 , . . . , x n − 1 ) y ⃗ \vec{a}=V^{-1}(x_0,x_1,...,x_{n−1})\vec{y}

多项式乘法

已知多项式 A ( x ) , B ( x ) A(x),B(x) ，要求多项式 C ( x ) = A ( x ) ∗ B ( x ) C(x)=A(x)*B(x) ，这就是多项式乘法

假如 A ( x ) , B ( x ) A(x),B(x) 基于系数表达
那么 c ⃗ \vec{c} 的每一项为 c i = ∑ j = 0 i a j ∗ b i − j c_i=\sum_{j=0}^ia_j*b_{i-j} ，复杂度为 O ( n 2 ) O(n^2)

那么基于点值表示呢
对于一个给定的值 x = x 0 x=x_0 ，有 C ( x 0 ) = A ( x 0 ) ∗ B ( x 0 ) C(x_0)=A(x_0)*B(x_0) ，复杂度为 O ( n ) O(n)

这是明显的差距啊，也就是说计算多项式乘法显然点值表示更优

多项式的求值&&插值

将多项式的系数表示转化为点值表示即为求值
对于一个次数界为 n n 的多项式
计算一个点的值为 O ( n ) O(n) ，总共 n n 个点，复杂度为 O ( n 2 ) O(n^2)

相对的，将多项式的点值表示转化为系数表示即为插值
假如我们将插值表示成增广矩阵形式再对范德蒙德矩阵求逆来得到系数表达，显然复杂度 O ( n 3 ) O(n^3)

假如借助拉格朗日插值公式
f ( x ) = ∑ i = 0 n − 1 y i ( ∏ j ! = i x − x j x i − x j ) f(x)=\sum_{i=0}^{n-1}y_i(\prod_{j!=i}\frac{x-x_j}{x_i-x_j})
复杂度也依然是 O ( n 2 ) O(n^2)

从DFT && IDFT 到 FFT

看到这里，其实你已经懂得了 D F T DFT (离散傅里叶变换) 与 I D F T IDFT (逆离散傅立叶变换)

对于 A ( x ) A(x) 的系数表达 a ⃗ = ( a 0 , a 1 , . . . a n − 1 ) \vec{a}=(a_0,a_1,...a_{n−1})
定义结果 y k = ∑ i = 0 n − 1 a i ∗ x k i y_k=\sum_{i=0}^{n-1}a_i*x_k^i
则 y ⃗ = ( y 0 , y 1 , . . . y n − 1 ) \vec{y}=(y_0,y_1,...y_{n−1}) 就是系数向量 a ⃗ \vec{a} 的离散傅里叶变换，记为 y ⃗ = D F T n ( a ⃗ ) \vec{y}=DFT_n(\vec{a})

I D F T IDFT 则恰好相反，即 a ⃗ = I D F T n ( y ⃗ ) \vec{a}=IDFT_n(\vec{y})

现在计算DFT与IDFT复杂度都是 O ( n 2 ) O(n^2) ，不但与直接系数相乘复杂度一样，还常数贼大
不过介绍这么多肯定不会是没用的，接下来我们的FFT就要登场了

为了解决两种表示法转换的复杂度问题
F F T FFT 通过精心挑选求值点，可以让两种表示法的转换复杂度达到 O ( n l o g n ) O(nlogn)
所以我们概括出计算多项式乘法的策略

1. 求值：利用FFT在 O ( n l o g n ) O(nlogn) 时间内转换多项式为点值表达
2. 逐点相乘：利用基于点值表达的多项式O(n)计算多项式乘积
3. 差值：利用FFT在 O ( n l o g n ) O(nlogn) 时间内转换多项式为系数表达

单位复根

(注意理解此处需要一定的复数学习基础)

首先引入单位复根的定义

  • 对于满足 w n = 1 w_n=1 的复数 w w ，我们称其为 n n 次单位复根

根据其定义及复数运算法则不难得出 n n 次单位复根有 n n 个 这样的结论

若我们将其用向量在复平面上表示出来的话，会是像这样
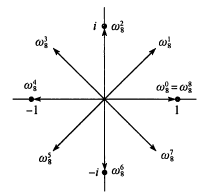
在这里插入图片描述
及在复平面上以原点为圆心，一单位长度为半径作圆
以原点为起点，圆的 n n 等分点为终点的向量，即为一个 n n 次单位根

那么如何计算这些单位根的值呢
这里就要用到史称最优美的数学公式——欧拉公式
e i x = cos ⁡ x   +   i sin ⁡ x e^{ix}=\cos x\ +\ i\sin x
(其中 i i 为虚数单位，即 i 2 = − 1 i^2=-1 )

我们尝试将 x = 2 π x=2\pi 带入
e i 2 π = cos ⁡ 2 π   +   i sin ⁡ 2 π = 1 = w n e^{i2\pi}=\cos 2\pi\ +\ i\sin 2\pi=1=w^n
w = e 2 π i n w=e^{\frac{2\pi i}{n}}

我们称此时的 w n = e 2 π i n w_n=e^{\frac{2\pi i}{n}} 为主 n n 次单位根
即上图中 幅角为正且最小的向量对应的复数
对于其他的单位根，我们记作 w n k = e 2 π i k n   ( 1 ≤ k ≤ n ) w_n^k=e^{\frac{2\pi i k}{n}}\ (1\leq k \leq n)
不难发现这些单位根都是主单位根的整数次幂，其中 w n n = 1 w_n^n=1

单位复根的引理

- 消去引理

引理：对任何整数 n ≥ 0 , k ≥ 0 , d > 0 n≥0,k≥0,d>0 有 w d n d k = w n k w_{dn}^{dk}=w_n^k
证明：直接带入上述定义即可
w d n d k = e 2 π i d k d n = e 2 π i k n = w n k w_{dn}^{dk}=e^{\frac{2\pi i dk}{dn}}=e^{\frac{2\pi i k}{n}}=w_n^k

- 折半引理

引理：对于任何大于0的偶数n，都有 n n 个 n n 次单位复根的平方的集合，等于 n 2 \frac{n}{2} 个 n 2 \frac{n}{2} 次单位复根的集合
证明：读起来很绕，但我们结合公式就好理解了
( w n k + n 2 ) 2 = w n 2 k + n = w n 2 k + w n n = w n 2 k = ( w n k ) 2 (w_n^{k+\frac{n}{2}})^2=w_n^{2k+n}=w_n^{2k}+w_n^n=w_n^{2k}=(w_n^k)^2
以复平面上的向量来理解就是方向相对的两组向量，其平方相等
这条引理就是FFT能折半解决问题的基础

快速傅里叶变换FFT

讲了这么久的前置姿势终于进入正题了
前面提到的 “精心挑选的求值点” 也就是 n n 个 n n 次单位根

下面为了讲解方便，设 n n 为2的整次幂
实际操作中若不足，则在高此项不断用系数为0的项补齐

对于多项式 A ( x ) = a 0 + a 1 ∗ x + a 2 ∗ x 2 + . . . + a n − 1 ∗ x n − 1 A(x)=a_0+a_1*x+a_2*x^2+...+a_{n-1}*x^{n-1}
我们将其每一项按奇偶项划分，设

A 1 ( x ) = a 0 + a 2 ∗ x + a 4 ∗ x 2 + ⋯ + a n − 2 ∗ x n 2 − 1 A1(x)=a_0+a_2∗x+a_4∗x^2+⋯+a_{n−2}∗x^{\frac{n}{2}-1}
A 2 ( x ) = a 1 + a 3 ∗ x + a 5 ∗ x 2 + ⋯ + a n − 1 ∗ x n 2 − 1 A2(x)=a_1+a_3∗x+a_5∗x^2+⋯+a_{n−1}∗x^{\frac{n}{2}-1}

那么显然有 A ( x ) = A 1 ( x 2 ) + x ∗ A 2 ( x 2 ) A(x)=A_1(x^2)+x*A_2(x^2)
我们需要求所有 A ( w n k ) , 1 ≤ k ≤ n A(w_n^k),1\leq k \leq n

尝试带入 w n k w_n^{k} 得
A ( w n k ) = A 1 ( w n 2 k ) + w n k ∗ A 2 ( w n 2 k ) A(w_n^{k})=A_1(w_n^{2k})+w_n^{k}*A_2(w_n^{2k})

再尝试带入 w n k + n 2 w_n^{k+\frac{n}{2}}
A ( w n k + n 2 ) = A 1 ( w n 2 k + n ) + w n k + n 2 ∗ A 2 ( w n 2 k + n ) A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}*A_2(w_n^{2k+n})
A ( w n k + n 2 ) = A 1 ( w n 2 k ∗ w n n ) − w n k ∗ A 2 ( w n 2 k ∗ w n n ) A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k}*w_n^n)-w_n^{k}*A_2(w_n^{2k}*w_n^n)
A ( w n k + n 2 ) = A 1 ( w n 2 k ) − w n k ∗ A 2 ( w n 2 k ) A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k})-w_n^{k}*A_2(w_n^{2k})

我们惊讶的发现这两个式子恰好只差一个符号
于是我们可以基于递归写出求值FFT

void FFT(complex* a,int len)//a是基于系数表达的向量a
{
    if(len==1) return;
    complex* a0=new complex[len>>1];
    complex* a1=new complex[len>>1];
    
    for(int i=0;i<len;i+=2)
    a0[i>>1]=a[i],a1[i>>1]=a[i+1];
    
    FFT(a0,len>>1); FFT(a1,len>>1);
    
    complex wn(cos(2*Pi/len),sin(2*Pi/len));//主n次单位根
    complex w(1,0);//辐角为2pi得单位根
    for(int i=0;i<(len>>1);++i)
    {
        a[i]=a0[i]+w*a1[i];//根据上述推导公式
        a[i+(len>>1)]=a0[i]-w*a1[i];
        w=w*wn;//得到下一个单位根
    }
    delete[] a0;
    delete[] a1;
}

插值FFT

上面我们通过FFT解决了求值
基于点值计算完多项式乘法后，再将其转换为系数表达就大功告成了

首先我们可以将求DFT过程结合范德蒙德矩阵表示出来
[ a 0 a 1 a 2 . . . a n − 1 ] ∗ [ 1 1 1 . . . 1 1 w n w n 2 . . . w n n − 1 1 w n 2 w n 4 . . . w n 2 ( n − 1 ) . . . . . . . . . . . . . . . 1 w n n − 1 w n 2 ( n − 1 ) . . . w n ( n − 1 ) ( n − 1 ) ] = [ y 0 y 1 y 2 . . . y n − 1 ] \left[ \begin{matrix} a_0 \\ a_1 \\ a_2 \\ ... \\ a_{n-1} \end{matrix} \right]*\left[ \begin{matrix} 1 &amp; 1 &amp; 1 &amp; ... &amp; 1\\ 1 &amp; w_n &amp; w_n^2 &amp; ... &amp; w_n^{n-1}\\ 1 &amp; w_n^2 &amp; w_n^4 &amp; ... &amp; w_n^{2(n-1)} \\ ... &amp; ... &amp; ... &amp;... &amp; ...\\ 1 &amp; w_n^{n-1} &amp; w_n^{2(n-1)}&amp;...&amp;w_{n}^{(n-1)(n-1)} \end{matrix} \right]=\left[ \begin{matrix} y_0 \\ y_1 \\ y_2 \\ ... \\ y_{n-1} \end{matrix} \right]
我们用 V n V_n 表示中间的范德蒙德矩阵，那么求值过程表示为 y ⃗ = V n a ⃗ \vec{y}=V_n\vec{a}
那么它的逆运算——插值，表示为 a ⃗ = V n − 1 y ⃗ \vec{a}=V_n^{-1}\vec{y} ( V n − 1 V_n^{-1} 为 V n V_n 的逆矩阵)
所以其实我们只要求出 V n − 1 V_n^{-1} 即可

现在我们再引入一个玄学定理

- 定理: 对于 j , k = 0 , 1 , . . . , n − 1 j,k=0,1,...,n−1 , V n − 1 V^{−1}_n 的 ( j , k ) (j,k) 处元素为 ω n − k j n ω_n^{\frac{−kj}{n}}

根据该引理我们得出 a k = 1 n ∑ i = 0 n − 1 y k ∗ w n − k i a_k=\frac{1}{n}\sum_{i=0}^{n-1}y_k*w_n^{-ki}
这与前面求值的公式 y k = ∑ i = 0 n − 1 a i ∗ x k i y_k=\sum_{i=0}^{n-1}a_i*x_k^i 仅仅次幂由正变负且多了一个 1 n \frac{1}{n} 项而已

所以我们在前面FFT代码上稍作修改即可同时求插值

void FFT(complex* a,int len,int opt)//opt==1求值，opt==-1插值
{
    if(len==1) return;
    complex* a0=new complex[len>>1];
    complex* a1=new complex[len>>1];
    
    for(int i=0;i<len;i+=2)
    a0[i>>1]=a[i],a1[i>>1]=a[i+1];
    
    FFT(a0,len>>1,opt); FFT(a1,len>>1,opt);
    
    complex wn(cos(2*Pi/len),opt*sin(2*Pi/len));//仅仅主次单位根不同
    complex w(1,0);
    for(int i=0;i<(len>>1);++i)
    {
        a[i]=a0[i]+w*a1[i];
        a[i+(len>>1)]=a0[i]-w*a1[i];
        w=w*wn;
    }
    delete[] a0;
    delete[] a1;
}

到这里FFT就可以以 O ( n l o g n ) O(nlogn) 的复杂度实现多项式乘法了
那么整个多项式乘法的FFT递归实现如下

#include<iostream>
#include<cmath>
#include<algorithm>
#include<map>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long lt;
typedef double dd;
 
int read()
{
    int f=1,x=0;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return f*x;
}

const dd Pi=acos(-1.0);
const int maxn=4000010;
int n,m;
struct complex{
    dd x,y;
    complex(dd _x=0,dd _y=0){ x=_x; y=_y;}
}A[maxn],B[maxn];
int lim=1;

//复数运算
complex operator +(complex a,complex b){ return complex( a.x+b.x, a.y+b.y);}
complex operator -(complex a,complex b){ return complex( a.x-b.x, a.y-b.y);}
complex operator *(complex a,complex b){ return complex( a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x);}

void FFT(complex* a,int len,int opt)
{
    if(len==1) return;
    complex* a0=new complex[len>>1];
    complex* a1=new complex[len>>1];
    
    for(int i=0;i<len;i+=2)
    a0[i>>1]=a[i],a1[i>>1]=a[i+1];
    
    FFT(a0,len>>1,opt); FFT(a1,len>>1,opt);
    
    complex wn(cos(2*Pi/len),opt*sin(2*Pi/len));
    complex w(1,0);
    for(int i=0;i<(len>>1);++i)
    {
        a[i]=a0[i]+w*a1[i];
        a[i+(len>>1)]=a0[i]-w*a1[i];
        w=w*wn;
    }
    delete[] a0;
    delete[] a1;
}

int main()
{
    n=read();m=read();
    for(int i=0;i<=n;++i) A[i].x=read();
    for(int i=0;i<=m;++i) B[i].x=read();
    
    while(lim<=n+m) lim<<=1;
    FFT(A,lim,1); FFT(B,lim,1);
    
    for(int i=0;i<=lim;++i) A[i]=A[i]*B[i];
    FFT(A,lim,-1);
    
    for(int i=0;i<=n+m;++i)
    printf("%d ",(int)(A[i].x/lim+0.5));//根据推到的公式还要除以n，加0.5是为了保证精度
    return 0;
}

但是你以为到这里就结束了？ 还没！
你会发现这份代码在luogu提交还是T一个点，是因为算法不对吗？不是

递归本身就自带大常数，而且每层还要额外申请空间，没有MLE还真是奇迹
FFT得优美性质远不止于此

给FFT来点优化吧——迭代与蝴蝶操作

首先我们可以注意到, 在上面的实现代码中计算了两次 ω n k ∗ y k [ 1 ] ω^k_n*y^{[1]}_k
复数运算是自带大常数的，我们可以将它只计算一次并将结果放在一个临时变量中

for(int i=0;i<(len>>1);++i)
{
    int t=w*a1[i];
    a[i]=a0[i]+t;
    a[i+(len>>1)]=a0[i]-t;
    w=w*wn;
}

好了，优化到此结束 呸，怎么可能
讲这里只是为了引入蝴蝶操作

-蝴蝶操作

我们定义 w n k w^k_n 为旋转因子
那么每一次先将 y k [ 1 ] y^{[1]}_k 与旋转因子的乘积存储在一个变量t里
并在 y k [ 0 ] y^{[0]}_k 增加、减去t的操作称为一次蝴蝶操作

接下来，为了避免递归带来的大常数我们自然想到迭代
尝试画出递归调用的递归树
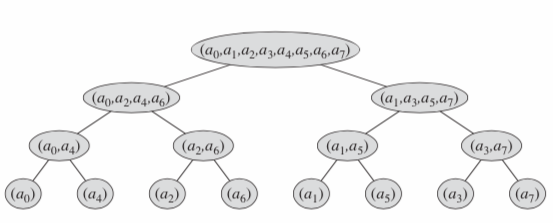
在这里插入图片描述
如果将初始向量按照叶子的位置预先排序好的话, 就可以自底向上一步一步合并结果

首先成对取出元素,
对于每对元素进行 1 次蝴蝶操作计算出它们的 D F T DFT 并用它们的 D F T DFT 替换原来的2个元素,
这样 a ⃗ \vec{a} 中就会存储有 n / 2 n/2 个二元 D F T DFT

继续成对取出元素,
对于每对元素进行 2 次蝴蝶操作计算出它们的 D F T DFT 并用它们的 D F T DFT 替换原来的4个元素,
这样 a ⃗ \vec{a} 中就会存储有 n / 4 n/4 个四元 D F T DFT

…

如此反复，直到计算出 2 个长度为 n / 2 n/2 的 D F T DFT , 最后使用 n/2 次蝴蝶操作即可计算出整个向量的 D F T DFT

假设一开始 a ⃗ \vec{a} 已按递归树最低层顺序排序，上述操作不难实现，只需要三层循环

for(int i=1;i<lim;i<<=1)//枚举当前已计算的DFT长度
{
    complex wn(cos(Pi/i),opt*sin(Pi/i));
    for(int j=0;j<lim;j+=(i<<1))//枚举每个DFT的开始位置
    {
        complex w(1,0);
        for(int k=0;k<i;++k)//枚举每个DFT内的偏移量
        {
            complex nx=a[j+k],ny=w*a[i+j+k];//蝴蝶操作
            a[j+k]=nx+ny;
            a[i+j+k]=nx-ny;
            w=w*wn;
        }
    }
}

最后一个要解决的问题就是对 a ⃗ \vec{a} 排序了
我们观察排序前后的变化

原来的序号 0 1 2 3 4 5 6 7
现在的序号 0 4 2 6 1 5 3 7
原来的二进制表示 000 001 010 011 100 101 110 111
现在的二进制表示 000 100 010 110 100 101 011 111

发现它们的二进制表示正好是反序，这就是蝴蝶定理
我们只要一开始 O ( n ) O(n) 处理好其对应位置即可

for(int i=0;i<lim;++i)
R[i]= (R[i>>1]>>1) | ( (i&1) << (L-1) ) ;

最后迭代FFT代码呈上

#include<iostream>
#include<cmath>
#include<algorithm>
#include<map>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long lt;
typedef double dd;
 
int read()
{
    int f=1,x=0;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return f*x;
}

const dd Pi=acos(-1.0);
const int maxn=4000010;
int n,m;
struct complex{
    dd x,y;
    complex(dd _x=0,dd _y=0){ x=_x; y=_y;}
}A[maxn],B[maxn];
int lim=1,L,R[maxn];

complex operator +(complex a,complex b){ return complex( a.x+b.x, a.y+b.y);}
complex operator -(complex a,complex b){ return complex( a.x-b.x, a.y-b.y);}
complex operator *(complex a,complex b){ return complex( a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x);}

void FFT(complex* a,int opt)
{
    for(int i=0;i<lim;++i)
    if(i<R[i]) swap(a[i],a[R[i]]);
    
    for(int i=1;i<lim;i<<=1)
    {
        complex wn(cos(Pi/i),opt*sin(Pi/i));
        for(int j=0;j<lim;j+=(i<<1))
        {
            complex w(1,0);
            for(int k=0;k<i;++k)
            {
                complex nx=a[j+k],ny=w*a[i+j+k];
                a[j+k]=nx+ny;
                a[i+j+k]=nx-ny;
                w=w*wn;
            }
        }
    }
}

int main()
{
    n=read();m=read();
    for(int i=0;i<=n;++i) A[i].x=read();
    for(int i=0;i<=m;++i) B[i].x=read();
    
    while(lim<=n+m) lim<<=1,L++;
    for(int i=0;i<lim;++i)
    R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));
    
    FFT(A,1); FFT(B,1);
    for(int i=0;i<=lim;++i) A[i]=A[i]*B[i];
    
    FFT(A,-1);
    for(int i=0;i<=n+m;++i)
    printf("%d ",(int)(A[i].x/lim+0.5));//根据推倒的公式除以n
    return 0;
}

最后的闲(tu)话(cao)

作为一个数论蒟蒻还真是第一次接触这么难的东西
为了学FFT自己花了三天恶补了一堆选修
到最后其实还是有很定理不能自证，只能记结论直接用，等哪天突然开悟了再一点点补上吧
若还有什么解释错误的地方希望dalao们指出QAQ

附上一些蒟蒻学习FFT时一些比较好的参考blog L i n k 1 Link1 , L i n k 2 Link2 , L i n k 3 Link3

猜你喜欢

转载自blog.csdn.net/niiick/article/details/85378959
今日推荐
Apache Doris 2.0.10 版本正式发布！
开源日报 | 大模型开战；大模型独角兽被曝卖身；周鸿祎建议谷歌开源所有产品；最大开源AI社区提供1000万美元共享GPU
开源日报 | Chrome内置Gemini的意义不在于Gemini；中国AI追随之路的五大误区；ECharts创始人“下海”养鱼；谷歌I/O开发者大会什么都有，只是没有惊喜
微软回应中国区AI团队“打包赴美”传闻
基于大语言模型的开源知识库问答系统 MaxKB GitHub Star 数量突破 5,000 个！
美国拟限制 AI 大模型出口中国和俄罗斯
苹果将与 OpenAI 达成协议，将 ChatGPT 应用于 iPhone
周排行
阿里云短信服务平台注册
Windows下的字符串处理(1)
sqoop: mysql导入数据到hdfs, hive, hbase
commons.lang中常用的工具类
离线安装PostgreSQL11.6
使用PyTorch简单实现卷积神经网络模型
一文彻底搞定谱聚类
一道面试题引发的血案
One Chat for Mac(聊天工具)
TCP/IP的底层队列是如何实现的？
每日归档
更多
2024-05-17(34)
2024-05-16(6)
2024-05-15(24)
2024-05-14(0)
2024-05-13(18)
2024-05-12(0)
2024-05-11(38)
2024-05-10(38)
2024-05-09(35)
2024-05-08(42)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022