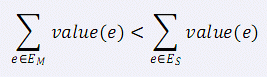题目p2023
描述 Description
小 C 最近学了很多最小生成树的算法,Prim 算法、Kurskal 算法、消圈算法等等。 正当小 C 洋洋得意之时,小 P 又来泼小 C 冷水了。小 P 说,让小 C 求出一个无向图的次小生成树,而且这个次小生成树还得是严格次小的,也就是说: 如果最小生成树选择的边集是 EM,严格次小生成树选择的边集是 ES,那么需要满足:(value(e) 表示边 e的权值)
这下小 C 蒙了,他找到了你,希望你帮他解决这个问题。
输入格式 Input Format
第一行包含两个整数N 和M,表示无向图的点数与边数。
接下来 M行,每行 3个数x y z 表示,点 x 和点y之间有一条边,边的权值为z。
输出格式 Output Format
包含一行,仅一个数,表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
样例输入 Sample Input
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
样例输出 Sample Output
11
时间限制 Time Limitation
1s
注释 Hint
数据中无向图无自环; 50% 的数据N≤2 000 M≤3 000; 80% 的数据N≤50 000 M≤100 000; 100% 的数据N≤100 000 M≤300 000 ,边权值非负且不超过 10^9 。
来源 Source
bzoj1977
题解
转自https://www.luogu.org/blog/user29519/solution-p4180
个人认为这篇题解有助于理解
一、总体思路
首先,我这一题的思路是倍增LCA+Kruskal
没学过这两个算法没关系,后面有讲解
时间复杂度O(nlog2n+mlog2m)
(倍增O(nlognn)+Kruskal O(mlog2m+mα(n)))
α(n)是阿克曼函数的反函数ack(),增长极慢,普通范围内大概在4以内
二、补习算法(会的请跳过)
1.倍增LCA
形象地说,倍增算法是一种“高级小抄”
假设我是一个小朋友考试要考1+n=?
我不会,于是我开始打小抄:
1+1=2
1+2=3
1+3=4
……
这是普通小抄
但是老师很坑,n<=210000
考试时:
老师:dijstra0分,站起来解释一下
dijstra:我用了IO优化,可是小抄只打了…
这时呢,倍增大佬横空出世
倍增大佬:我用 cin/cout 打完了
于是dijstra很佩服,付给倍增大佬210000 ,要求学习打小抄
倍增大佬:我把21−10000抄了下来,然后就GG了
树上倍增: 用bz数组存一下,bz[i][j]表示i点上面的第2j个祖先
1.预处理(伪代码)
for j 1 .. 18
for i 1 .. n
bz[i][j] = bz[bz[i][j-1]][j-1]
2.求LCA
LCA(u,v)
{
if < u的深度 小于 v的深度 >
{
swap(u , v);
}
for i 18 .. 0
if < u 向上跳还是 比 v 低 >
{
u 向上跳
}
if < u , v 重合>
{
return u
}
for i 18 .. 0
{
if < u 向上跳 , v 向上跳 未重合 >
{
u 向上跳
v 向上跳
}
}
return u
}
推荐题目
2.kruskal
kruskal是一种贪心最小生成树
不用并查集就会很慢
并查集(O(\alpha(n))O(α(n)))
路径压缩:代码只有一行,却是灵魂所在。它是在查询时’顺便’存一下
伪代码:
Father[N]
for i 1 .. N
Father[i] = i
//初始化
Get_Father( x )
{
if x=Father[x]
return x
else
return Father[x]=Get_Father(Father[x])
}
//路径压缩
Merge( u , v )
{
Father_u = Get_Father(u)
Father_v = Get_Father(v)
if Father_u != Father v
//不在一个联通块内
{
Father [ Father_u ] = Father_v
}
}
kruskal
将边按照边权排序
从小到大扫
不在联通块内就连边
伪代码
sort;
for i 1 .. m
{
if <不在同一联通快>
{
Merge
Ans+=边权
}
}
推荐题目
三、解决方案
1. 首先,kruskal求最小生成树
2. 求次小生成树
关键在于次小生成树怎么求:
问自己一些问题
怎么求不严格次小生成树
不严格次小生成树为什么不严格
仔细思考上面两个问题,然后带着问题阅读以下部分
dijstra:回归本质
扪心自问,kruskalkruskal 的本质是什么?
贪心
kruskal算法被证明,对于任何的u,v
有u到v之间边权最大值小于等于u到v未选入的边的边权
所以说,不严格次小生成树只要
遍历每条未选的边(u,v,d),用它替换u和v之间的最大边即可
现在我们的任务就是把不严格的不去掉
为什么它不严格?
因为
u到v之间边权最大值小于等于u到v未选入的边的边权
等于!
是不是感觉自己被坑了?
没关系,我们只要多存一个次大值即可
指出一句,attack的题解对次大值合并时有一处疏忽,他的代码会在合并两个相等的最大值时
最大=次大
一切最大次大都在倍增时处理
四、注意事项
开long long(int64)
inf开大(我开2147483647炸了)
评测结果
https://www.luogu.org/recordnew/show/15382208
代码
#include<bits/stdc++.h>
#define up(i,a,b) for (register ll i=a;i<=b;++i)
#define down(i,a,b) for (register ll i=a;i>=b;--i)
using namespace std;
typedef long long ll;
const ll N=4e5+10;
const ll M=9e5+10;
const ll inf=2147483647000000;
inline ll read()
{
ll f=1,num=0;
char ch=getchar();
while (!isdigit(ch)) { if (ch=='-') f=-1; ch=getchar(); }
while (isdigit(ch)) num=(num<<1)+(num<<3)+(ch^48), ch=getchar();
return num*f;
}
struct edge
{
ll x,y,z,next;
}G[N<<1],A[M<<1];
ll head[N],len;
inline void add(ll x,ll y,ll z)
{
G[++len].x=x,G[len].y=y,G[len].z=z,G[len].next=head[x],head[x]=len;
}
ll fa[N];
inline ll get(ll x)
{
if (x==fa[x]) return x;
return fa[x]=get(fa[x]);
}
ll bz[N][19],maxi[N][19],mini[N][19],deep[N];
inline void dfs(ll x,ll fa)
{
bz[x][0]=fa;
for (ll i=head[x];i;i=G[i].next)
{
ll y=G[i].y;
if (y==fa) continue;
deep[y]=deep[x]+1ll;
maxi[y][0]=G[i].z;
mini[y][0]=-inf;
dfs(y,x);
}
}
ll n,m;
inline void cal()
{
up(i,1,18)
up(j,1,n)
{
bz[j][i]=bz[ bz[j][i-1] ][i-1];
maxi[j][i]=max(maxi[j][i-1],maxi[ bz[j][i-1] ][i-1]);
mini[j][i]=max(mini[j][i-1],mini[ bz[j][i-1] ][i-1]);
if (maxi[j][i-1]>maxi[ bz[j][i-1] ][i-1])
mini[j][i]=max(mini[j][i],maxi[ bz[j][i-1] ][i-1]);
else if (maxi[j][i-1]<maxi[ bz[j][i-1] ][i-1])
mini[j][i]=max(mini[j][i],maxi[j][i-1]);
}
}
inline ll lca(ll x,ll y)
{
if (deep[x]<deep[y])
swap(x,y);
down(i,18,0)
if (deep[bz[x][i]]>=deep[y])
x=bz[x][i];
if (x==y) return x;
down(i,18,0)
if (bz[x][i]^bz[y][i])
x=bz[x][i],y=bz[y][i];
return bz[x][0];
}
inline ll qmax(ll x,ll y,ll maxnum)
{
ll ans=-inf;
down(i,18,0)
if (deep[bz[x][i]]>=deep[y])
{
if (maxnum!=maxi[x][i])
ans=max(ans,maxi[x][i]);
else
ans=max(ans,mini[x][i]);
x=bz[x][i];
}
return ans;
}
inline bool comp(edge x,edge y)
{
return x.z<y.z;
}
ll vis[M<<1];
int main()
{
n=read(),m=read();
up(i,1,m)
A[i].x=read(),A[i].y=read(),A[i].z=read();
sort(A+1,A+m+1,comp);
up(i,1,n)
fa[i]=i;
ll cnt=0ll;
up(i,1,m)
{
ll x=get(A[i].x);
ll y=get(A[i].y);
if (x==y) continue;
cnt+=A[i].z;
fa[x]=y;
add(A[i].x,A[i].y,A[i].z),add(A[i].y,A[i].x,A[i].z);
vis[i]=true;
}
mini[1][0]=-inf;
deep[1]=1;
dfs(1,-1);
cal();
ll ans=inf;
up(i,1,m)
if (!vis[i])
{
ll x=A[i].x,y=A[i].y,z=A[i].z;
ll l=lca(x,y);
ll maxx=qmax(x,l,z);
ll maxy=qmax(y,l,z);
ans=min(ans,cnt-max(maxx,maxy)+z);
}
printf("%lld",ans);
return 0;
}