ARCore之路－计算机视觉之机器学习（二）

版权声明：David Wang原创ARCore文章，仅供学习研究之用，不得用于任何商业目的，未经授权不得转载！ https://blog.csdn.net/yolon3000/article/details/84561120

  机器学习遇到的第一个模型便是线性回归，而且是一元线性回归，但这个最简单的模型却包含了很多的知识点，如矩阵计算、最小二乘、梯度下降等等。这是机器学习的入门，理解这些基本概念对后面的学习有极其重要的影响。在这篇文章中，我们主要对回归模型进行阐述，然后还会讨论梯度下降算法。我们力求通俗易懂，但数学应有的严谨性又不能不有所涉及，重在理解。

一、线性回归

  在统计学中，线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。通俗的讲，线性回归就是在给定一定量数据的情况下，通过分析找到一个最佳的线性方程来拟合所有的数据，并以此方程作为模型来预测未知数据。 回归属于有监督学习中的一种方法。该方法的核心思想是从连续型统计数据中得到数学模型，然后将该数学模型用于预测或者分类。在监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面。

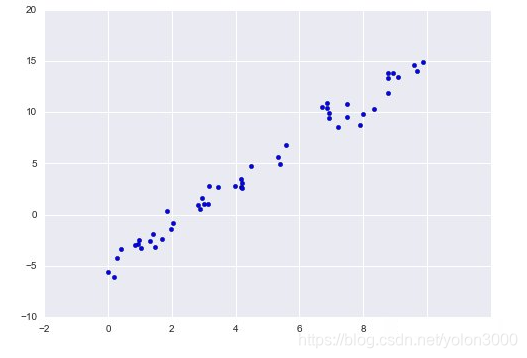
  线性回归原理是根据连续统计数据情况下，选取大量的样本数据，如上图所示，根据这些样本的趋势，选择合适的假设函数，此处选择的是线性回归的假设函数。根据样本，计算代价函数的极小值，此时的θ值就是我们需要得到的数学模型的参数值，同时，这个假设函数即为我们要选取的数据模型。在选择这个线性模型中，理想情况是能够尽量符合所有样本的数学模型。当然，一般情况下很难找到这个全拟合的模型，因此，我们需要找到尽可能符合当前统计数据的数学模型来代替。并使样本在数学模型中的误差平方和最小，这也就产生了代价函数。我们只需要找到代价函数的极小值，此时的θ代入到假设函数中，我们就得到了比较符合要求的数学模型。

  在上图中，我们可以用一条曲线去尽量准的拟合这些数据，这条曲线不一定能符合每一个样本点，但其方差值最小，这条曲线即为我们寻找的数据模型，这样，我们就可以根据这条曲线的情况来预测在x轴的某点对应的y轴上的值。   线性回归已经存在多年，并且被认为是解决许多统计数据分析问题的基础，它是许多其他机器学习的基础。对于上图，在不深入了解数学细节的情况下，只需要理解这条线是为了最小化回归曲线和样本点之间的误差，这通常是称为最佳拟合线或使误差最小化的线。需要指出的是，概率和统计在各种形式的机器学习中都发挥着重要作用，良好的概率与统计知识将地机器学习起到很好的帮助作用。   根据我们刚学习的知识，下面介绍典型的机器学习的过程。首先给出一个输入数据（样本），我们的算法会通过一系列的过程得到一个估计的函数（训练），这个函数有能力对没有见过的新数据给出一个新的估计，也被称为构建一个模型。如下图所示：

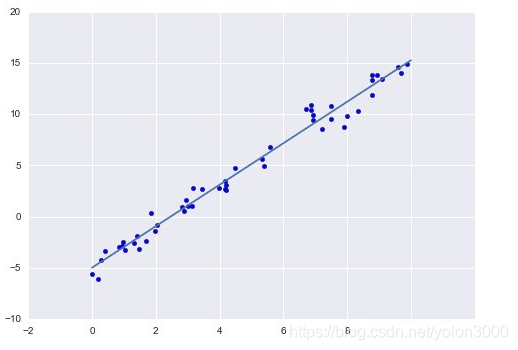
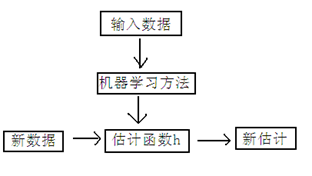
   线性回归假设特征点（样本值）和结果满足线性关系。其实线性关系的表达能力非常强大，每个特征对结果的影响强弱可以由前面的代价函数参数体现，而且每个特征变量可以首先映射到一个函数，然后再参与线性计算。这样也可以表达特征与结果之间的非线性关系。
   对上图，我们用X1，X2…Xn 去描述特征点（样本值）里面的分量，比如x1=售价，x2=重量等等，我们可以做出一个估计函数：

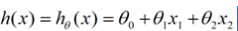
   θ在这儿称为参数，在这的意思是调整特征点（样本值）中每个分量的影响力，即哪个分量更重要。如果我们令X0 = 1，就可以用向量的方式来表示了：

   我们程序需要一个机制去评估我们θ是否最优，这就需要对我们做出的h函数进行评估，一般这个函数称为损失函数（loss function）或者错误函数(error function)，其用来描述h函数好不好的程度，在下面，我们称这个函数为J函数，这个J函数如下：    这个错误估计函数是去对x(i)的估计值与真实值y(i)差的平方和作为错误估计函数，前面乘上的1/2是为了在求导的时候消除参数。 如何调整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)和梯度下降法。

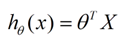
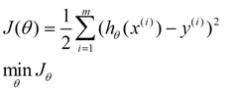
二、梯度下降算法

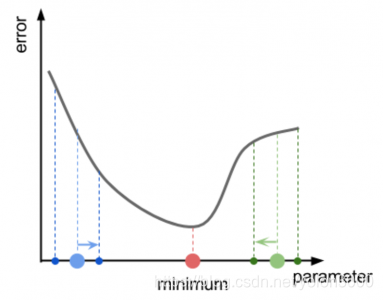
   在选定线性回归模型后，只需要确定参数θ，就可以将模型用来预测。然而θ需要在J(θ)最小的情况下才能确定，因此问题归结为求极小值问题。梯度下降法（Gradient descent）最大的问题是求得的值有可能不是全局极小值，这与初始点的选取有关。理解梯度下降运作方式的恰当比喻是想象一个丘陵地形，我们立在一个随机点，并且想抵达整个丘陵的最低点。我们叫它地形最小值。每一步，梯度下降向所在高度的更低位置移动。如果地形的几何结构相对简单，这个方法将会向着谷底靠拢。下图展示一个梯度下降的成功案例。案例中，我们有一个单参（X轴）函数，返回误差值（Y轴），从X轴随机点开始（蓝和绿点），梯度下降应该迫使我们向最小值方向移动（蓝和绿箭头）。

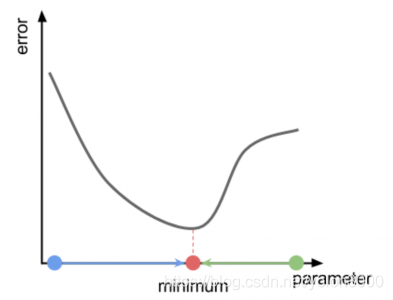
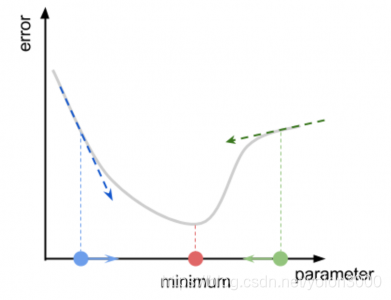
   在上例中，我们移动的方向是显而易见的。然后，因为梯度下降没有最小值在哪里的先验知识，算法能做到的最佳猜测就是沿着斜率的方向移动，也称作函数的斜率。理想情况下，跟着斜率就可以走到山谷。下图展示了两个不同点的误差函数的斜率：

   为使梯度下降算法有效，我们想得到的最小化函数应该满足特定的属性。如果地形函数相对平滑，就会有更高几率使梯度下降成功。在不连续或有许多峰峦的地形上，我们可能不得不为了到达山谷底部而走一段很长很长的路。

   斜率估算
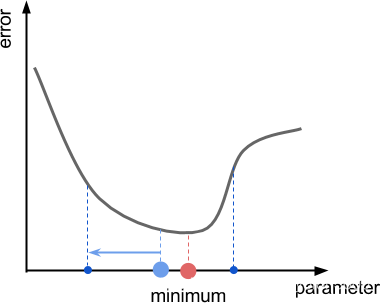
   函数的斜率和它的导数密切相关。然而计算导数，要求函数满足特定的数学属性，不是所有函数都有导数。此外，导数的分析推导需要有分析的误差函数。在一些问题中，有时得到函数的导数是不可能的。因此解决方法是得到这个值的匡算（粗略估计）。下图展示了一维简单函数中我们通过附近采样点并计算局部斜率。如果左边的误差函数更小，则向左。如果右边的误差函数更小，则向右。

   斜率和导数
   斜率和导数的概念是有严格的相互关联性的。函数的斜率或者方向导数是指向最陡上升方向的向量。在单维函数中（就像图中显示的那样）随着函数起伏，斜率要么是+1 要么是-1 。函数的导数是一个在它的斜率方向上移动时，表明函数上升的有多快的数值。我们的目的不是计算出函数的真实斜率。相反，我们提供一个预估，预估斜率是一个矢量，表示方向或是最陡上升方向。

   抽样
   采样距离对估计会产生很大影响，如下图所示，采样距离过大会产生右侧的高度比左侧高的错觉，这将会引向了错误的方向。减少采样距离可以弱化这个问题，但是依然没有办法完全避免。对于一个解决方案来说，更小的采样距离导致更慢的收敛速度（当然，这个问题可以通过采取更高级的梯度下降法来解决）。

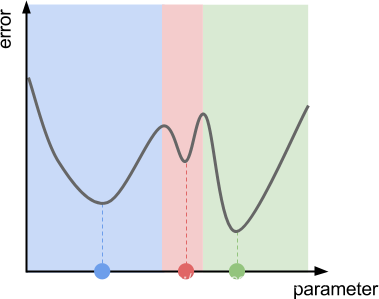
   几个局部最小值

   梯度下降算法并不能保证找到极小值，如下图所示：

   在上图函数中。函数有三个局部最小值，代表着三个不同的极小值。如果我们使用绿色区域的点来初始化梯度下降，我们会在绿色区域的谷底停住。这同样适用于红色和蓝色区域（这个问题可以通过采取更高级的梯度下降法来解决）。

   数学原理
   梯度下降是一种数学运算。第一步是计算在特定点p上误差函数的斜率f，因为函数的斜率和它的导数密切相关。由此，我们比较好的切入点是求取误差函数在某位置导数，f的导数被称为f’，它表示函数f的发展速率。并且具有以下属性：

• $f'(p)>0$ 则函数f上升；
• $f'(p)<0$ 则函数f下降；
• $f'(p)=0$ 则函数f平行；

下图直观的展示了导数与斜率的关系。

   我们关心的是需要采样的两点之间的误差函数的导数。dx是我们在前文中介绍的采样距离。函数的实际导数需要使用一个极限来进行计算，在计算梯度时使用足够小的采样距离来对导数进行估计。

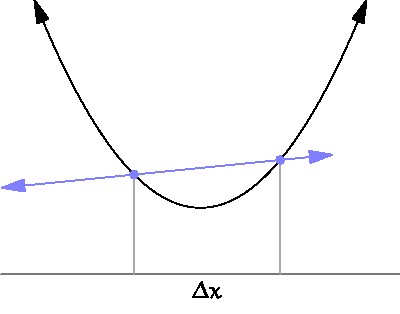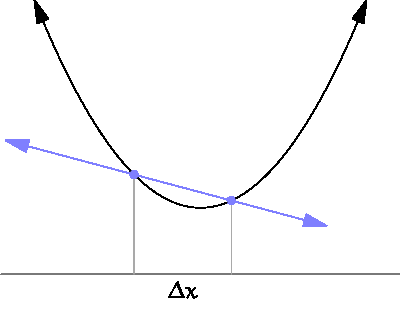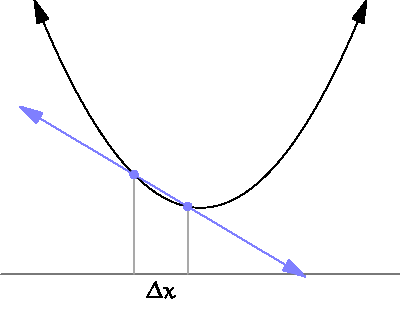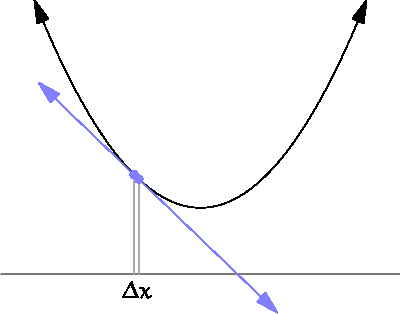
三、最小二乘法

   最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配，利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小，最小二乘法还可用于曲线拟合。
   以最简单的一元线性模型来解释最小二乘法。对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：
   （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
   （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
   （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。
   最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

参考文献

1、An Introduction to Gradient Descent An Introduction to Gradient Descent