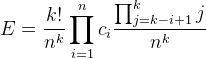大致题意:给出一个数列{an},每次随机的选择一个数字ai,产生出了ai之外其余所有数字之积的贡献,然后ai减一。现在进行k次这样的操作,问最后者k次操作产生的贡献之和是多少。
这个贡献看起来很复杂,但是实际上,我们可以把每一次操作的贡献,看作是操作前后所有数字的乘积之差。具体推导如下:
这样我们就证明了一次操作前后的贡献就是操作前后两次所有数字乘积的差。那么,显然多次操作中间的乘积可以抵消,最后的贡献就是初始时所有数字的乘积与最终所有数字的乘积。初始所有数字的乘积已知,我们要求贡献之和的期望,相当于只需要求最终乘积的期望。
我们考虑每个数字被选中{bi}次,那么这个数字最后的贡献就是ai-bi,显然Σbi=k。那么我们可以写出最后乘积的期望的表达式:
接下来考虑这个式子怎么求。这里的{bi}是每个位置数字被取的次数,这个次数的取值在区间[0,k]上,对于每一个取值,我们都对应一个(ai-bi)/bi的数值。我们令f表示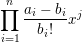


对于这个ai-x由于n比较小,所以我们可以暴力O(N^2)直接去展开成一个多项式。可以得到Π(ai-x)=Σci(x^i)。那么有:
现在我们回顾一下,我们要求的东西到底是什么。我们要求的是进行k次操作之和的贡献之和的期望。那么这个期望在f的生成函数中怎么体现呢?注意到我们之前是按照进行操作的次数展开的,x的k次项的系数表示取k次的方案数。所以说我们要求的就是x的k次项的系数。
进行到这一步,我们可以考虑再次把e^(nx)给展开,于是就变成了两个多项式的卷积。可以知道x的课次项系数是:
如此我们就可以算出x的k次项的系数。有了系数之后,我们考虑把[x^k]f回代入E的表达是,也即把前面的系数乘上,得:
最后用初始的乘积减去这个E即可。时间复杂度只要在O(N^2)展开得到{ci}的时候,其余都是O(N)。总体来说这题比较巧妙的运用了幂级数型生成函数和指数型生成函数两种生成函数,使得在推导的过程中能够相互转换,变成简单形式后暴力求解,最后再回代。具体见代码:
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int mod = 1e9 + 7;
const int modinv2 = 5e8 + 4;
const int G = 3;
const int N = 5010;
int fac[N],ifac[N],inv[N],pw[N];
int a[N],b[N],c[N],n,k;
void init()
{
fac[0]=ifac[0]=inv[0]=1;
fac[1]=ifac[1]=inv[1]=1;
for(int i=2;i<N;i++)
{
fac[i]=fac[i-1]*(LL)i%mod;
inv[i]=(mod-mod/i)*(LL)inv[mod%i]%mod;
ifac[i]=ifac[i-1]*(LL)inv[i]%mod;
}
}
int main()
{
LL ans=1;
init(); pw[0]=1;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
ans=ans*a[i]%mod;
pw[i]=(LL)pw[i-1]*n%mod;
}
//cout<<ans<<endl;
c[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<i;j++) b[j]=(LL)c[j]*a[i]%mod;
for(int j=0;j<i;j++) b[j+1]=(b[j+1]-c[j]+mod)%mod;
memcpy(c,b,sizeof(c));
}
for(int i=0,t=1,T=1;i<=n;i++)
{
//cout<<c[i]<<' ';
c[i]=(LL)c[i]*t%mod*T%mod;
t=(LL)t*inv[n]%mod; T=(LL)T*(k-i)%mod;
}
//cout<<endl;
for(int i=0;i<=n;i++) ans=(ans-c[i]+mod)%mod;
printf("%lld\n",(ans+mod)%mod);
return 0;
}
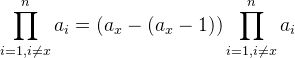
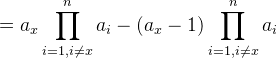
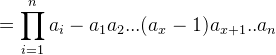
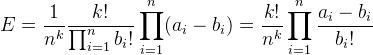
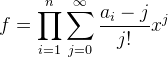
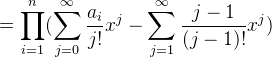
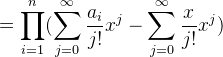
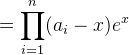

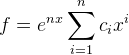
![[x^k]f=\sum_{i=0}^{n}c_{i}\frac{n^{k-i}}{(k-i)!}](https://img-blog.csdnimg.cn/20181227110927990)