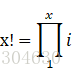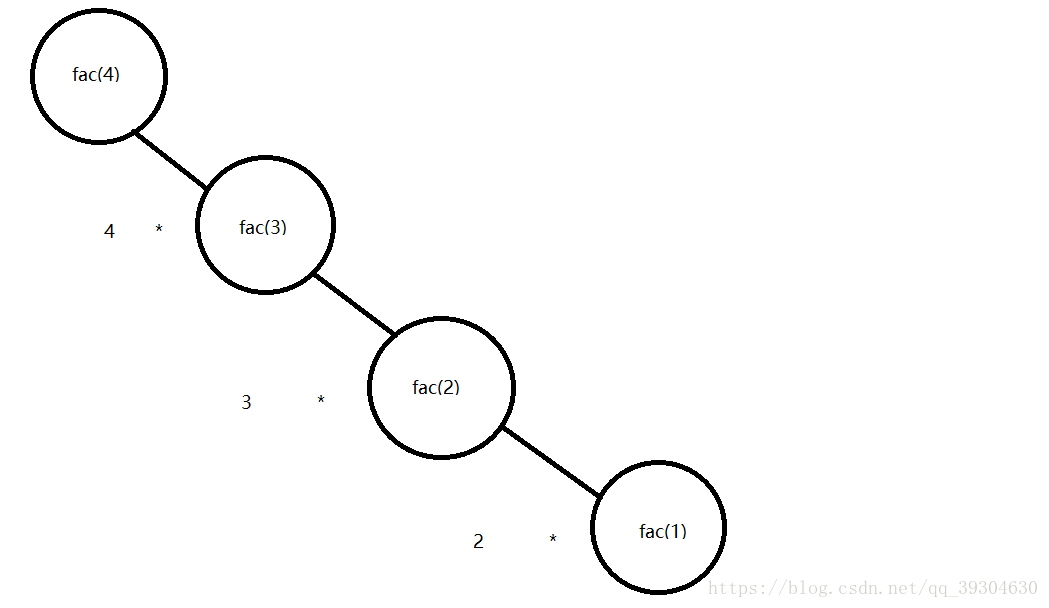其实从严格意义上说,动态规划,并不是一种算法,而是一种编程技巧,除去无关运算,降低时间复杂度。
举个例子:
经典例子1-阶乘:
递归实现:fac(x)=x*fac(x-1),临界条件为x==0时,返回1。
以x==4时,解空间树:
递归时由上往下延展,解问题时从下往上。
经典例子2-斐波那契:
fib(x)=fib(x-1)+fib(x-2)。
用递归的方式描述为:
#include<cstdio>
using namespace std;
int fib(int x){
if(x<=1)return 1;
else return fib(x-2)+fib(x-1);
}
int main()
{
int n;
scanf("%d",&n);
printf("%d",fib(n));
return 0;
}
我们假设n为4,那么在跑dfs的时候,生成的解空间树为:
我们可以观察到
1.虽然有生成2^(n-1)个节点,但是实际上有很多节点进行了重复的运算[这棵树有两个Fib(2)和三个Fib(1)]。
2.所有的中间节点在自己所在链未延伸到叶子的时候都是未知解的,但是在伸展到叶子节点时,触碰到了边界条件,最终所有的值都是从叶子向上回填的,解决的问题的规模逐渐变大,因此才触发了从小规模向大规模计算以优化dfs的动态规划技巧。
经典例题3-汉诺塔:【下面将逐步开始讲一些隐藏在条件内的动态规划】
汉诺塔的问题是给三根杆子A,B,C,在A上有n个盘子,要求你把这n个盘子放到C上去,盘子之间有大小关系,刚开始在A上的盘子从上至下是从小到大的,不能把大盘子放到小盘子之上。
我们先以n=3为例分析一下过程:
1.先将1从A->C
2.然后将2从A->B
3.再将1从C->B
4.最后将3从A->C
于是,当C上有一个盘子之后,B上累加有n-1个盘子,现在我们完全可以把B当作A’,将A当作B‘,于是问题变成了将A‘上的n-1个盘子放到C上。
总结一下过程:
1.先将n-1个盘子从A->B
2.将n号盘子从A->C
3.将n-1个盘子从B->C
于是问题的规模公式为T(n)=T(n-1)+1+T(n-1)->T(n)=2*T(n-1)+1。
边界条件为:T(1)=1。
反推得到T(n)=2^n-1,即为汉诺塔在n规模下需要的最小步数。
正常会对1步骤有疑问,因为在递归过程里他们没有显式表现出来,但是实际上由于解决1步骤的过程和3步骤是一样的,因此直接当作是一个子问题的递归过程就行。由于C杆上放的是每次递归规模下的最大盘子,因此什么盘子都可以放上去,就可以把它当作是空的。
经典例子4-打印所有序列:给你一个串,求出他的所有子集串。
所有子集?离散数学中称之为幂集。元素个数必定为2^n。
证明:对于每个元素,都有选择和不选两种抉择,n个元素的选择状态就会有2^n。【可以用二进制思考】
经典例子5-求牛的数量:第一年有一头牛,每头牛在第三年可以生小牛,求第n年有多少头牛。
经典例子6-数字路径:一个二维数组,每次可以选择向右或者向下,求一条路径,使得从左上角到右小角经过的数字和最小。
对于任意一个非边界位置位置(i,j),每次可以选择走(i+1,j)或者(i,j+1)。
我们来看看重复计算,以2*3的矩阵为例:
7 2 3
6 4 9
递归的解空间树:
显而易见,有重复的待求解状态状态。
这里我们可以普及几个名词了:
无后效性:当我们要求(2,2)->(2,3)的最短路径大小时,对于(1,1)来说,他可以通过向右再向下(1,1)->(1,2)->(2,2)到达该点,也可以通过先向下后向右(1,1)->(2,1)->(2,2)到达该点。无效性指的是(2,2)->(2,3)的最短路径的求解与如何从(1,1)->(2,2)的过程无关。
重复计算:在朴素递归中,由于不会记录已经计算过的小状态,所以当第二次碰到的时候,依旧得重新算一次,属于重复的冗余计算。
经典例子7-凑数:有一个数组,现在给出目标和值aim,问是否可从这些初中选出一些数,正好能凑出数aim。
当我们从这些数中选数的时候,实际上对于任意一个数,都有两种选择(选或不选)
#include <cstdio>
int Arr[105];
bool isOk[105][105];
int main() {
int n,aim,sum=0;
scanf("%d%d",&n,&aim);
for(int i=1;i<=n;i++){
scanf("%d",&Arr[i]);
sum+=Arr[i];
}
isOk[n][aim]=true;
for(int i=n-1;i>=0;i--){
for(int j=sum;j>=0;j--){
if(j+Arr[i+1]<=sum)
isOk[i][j]=isOk[i+1][j]||isOk[i+1][j+Arr[i+1]];
else isOk[i][j]=isOk[i+1][j];
}
}
printf("%s",isOk[0][0]?"Ok":"NotOk");
return 0;
}经典例子8-凑硬币:
你有1元,2元,5元硬币各无数个,现在给出x,要求你用最少的硬币凑出x块钱。
对于每个规模n,分别求dfs(n-1)、dfs(n-2)、dfs(n-5),分别表示在有n-1时拿1个1元、在有n-2时拿1个2元、在有n-5时拿1个5元:
边界条件:
1.如果规模n<0,表示不可行解,则忽略此种情况
2.如果规模n=0,表示正好凑数了原问题n的解
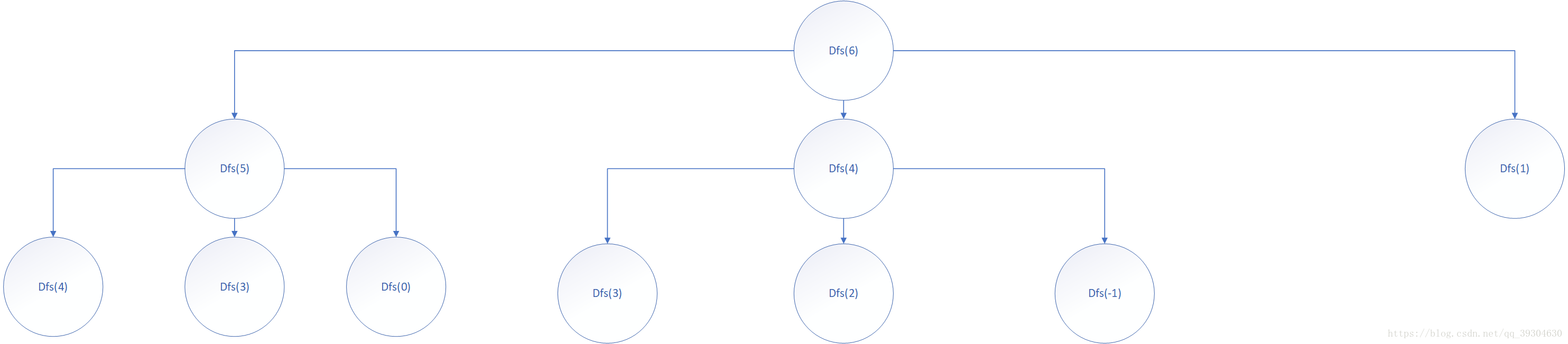
以x=6为例,解空间树为:
太庞大了,博主懒得画完了>-<,反正可以显然看出这里有很多的重复计算。
经典例子9-最长上升子序列:
有一个数串,先在要求你找出一个序列,使得这个序列保持单调递增性,并且给出最大的长度。
思路:假设我们考虑以Ai为结尾元素,用Bi表示以Ai结尾的最长上升序列的长度,当我们要求Bi+1的时候,我们需要用索引index遍历一遍B数组前面的i个数,如果Aindex<Ai+1,那么就可以把Aindex所拥有的最长上升子序列后面接上Ai+1得到Bi+1,在这i个数中求最大值即可,时间复杂度O(n^2)。
优化:如果我们已经有了长度为len的序列,为了使得这个序列更长【后面可接上的数更多】,那就要求在这个长度下的结尾元素尽可能的小。我们设array[i]表示长度为i时,最小的结尾元素。因此当考虑Ai+1的时候,对array数组二分,更新array即可,最长上升子序列长度就是array数组的长度。
改:最长非下降子序列:用upper_bound()得到第一个比自己大的数即可。
改2:最长非上升子序列:可以用映射将数据的大小关系逆转,就变成了一个最长非下降子序列问题。
经典例子10-最长公共子序列
给两个串,求他们的最长公共子序列。
思考:
1.如果Ai==Bj,那么我们只要知道A1~Ai-1和B1~Bj-1的最长公共子序列即可。
2.如果Ai!=Bj,那么我们应该求的是A1~Ai-1与B1~Bj的最长公共子序列长度和A1~Ai与B1~Bj-1的最长公共子序列长度的大值。