深入浅出极大似然估计法

之前多次接触极大似然估计，一直没有透彻的理解清楚，下午特意抽空查阅资料，整理成一篇较为通俗易懂的博文。

概念
　　“似然” ( likelihood )可以通俗的理解成 ”像是这样“ ，意思为 ”事件(观察数据)发生的可能性“，”极大似然估计“ 就是要找到一个估计值，使得 ”事件发生的可能性“ 最大。

举个例子
黑白球
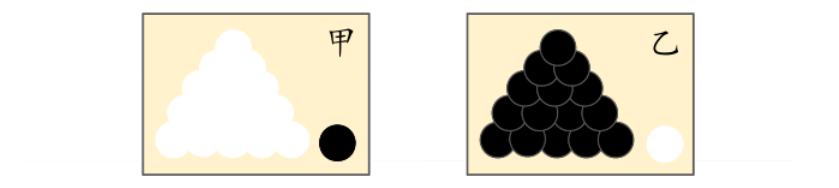
　　如图，有两个外形完全相同的箱子。甲箱中有99个白球1个黑球，乙箱中有99个黑球1个白球。一次试验，取出的是黑球。那么这个黑球最像是从哪个箱子取出的？大多数人都会说，这个黑球最像是从乙箱中取出的，这个推断符合人们的经验，即为“最大似然”。

总结来说，最大似然估计假设模型是确定的，然后利用抽取的样本结果，反推最大概率导致这样结果的模型参数值，即：“模型已定，参数未知”。

因此，样本结果的概率(即事件发生的可能性)，是一个带模型参数的似然函数。最大似然估计法的目标就是最大化似然函数，用最优化算法求解导致样本结果概率最大的参数值。

极大似然估计的描述
　　极大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。

首先，假设$ x_1,x_2,…,x_n$为独立同分布的采样，θ为模型参数, f 为所使用的模型。因此，产生上述采样结果的概率可表示为：

$f(x_1,x_2,...,x_n|\theta) = f(x_1|\theta)*f(x_2|\theta)...,f(x_n|\theta)$

由于极大似然估计法中，我们已知的为$ x_1,x_2,…,x_n$，未知为θ，故似然函数定义为:

$L(\theta|x_1,...,x_n) = f(x_1,...,x_n|\theta)=\prod_{i=1}^{n}f(x_i|\theta)$

两边取对数，得到对数似然，公式为：

扫描二维码关注公众号，回复： 4479423 查看本文章

$ln L(\theta|x_1,...,x_n) = ln \prod_{i=1}^{n}f(x_i|\theta) = \sum_{i=1}^nln f(x_i|\theta)$

最大似然估计法最常用的为对数平均似然，公式为：

$\hat{l} = \frac1{n}\ln L(\theta|x_1,...,x_n)$

因此最大似然估计法就是最大化似然函数求参数值，即：

$\hat{\theta}_{mle} = argmax_{\theta\in\Theta} \hat{l}(\theta|x_1,...,x_n)$

极大似然估计的例子
　　我们假设已知的模型为正态分布 $N(\mu,\sigma^2)$ ，则似然函数为：

$L(\mu,\sigma^2)=\prod_{i=1}^{n}f(x_i|\theta)=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}} =(2\pi\sigma^2)^{-\frac{n}{2}}e^{-\frac1{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2}$

两边取对数，得对数似然函数为：

$ln L(\mu,\sigma^2)=-\frac{n}{2}ln(2\pi)-\frac{n}{2}ln(\sigma^2)-\frac1{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2$

最大化似然函数，我们对它进行求导：

$\left\{\begin{array}{c}\frac{\partial\ln L(\mu,\sigma^2)}{\partial\mu}=\frac1{\sigma^2}\sum_{i=1}^{n}(x_i-\mu) = 0 \\ \frac{\partial\ln L(\mu,\sigma^2)}{\partial\sigma^2} = -\frac{n}{2\sigma^2}+\frac1{2\sigma^4}\sum_{i=1}^{n}(x_i-\mu)^2 = 0 \end{array}\right.$

联合解得：

$\left\{\begin{array}{c}\mu^*=\overline{x}=\frac1{n}\sum_{i=1}^{n}x_i \\ \sigma^{*2}=\frac1{n}\sum_{i=1}^n(x_i-\overline{x})^2 \end{array}\right.$

似然方程有唯一解： $(\mu^*,\sigma^{*2})$ ,即为最大似然估计量 $\hat{\theta}$ 。

因此，求最大似然估计量 $\hat{\theta}$ 的一般步骤为：

    （1）写出似然函数；

    （2）对似然函数取对数，并整理；

    （3）求导数；

    （4）解似然方程。

注意：

参数估计不同于估计。
　　日常所说的估计一般是通过样本分布估计总体的分布，比如用样本集的均值作为总体的期望。在参数估计中，模型是假设已知的，估计得参数后就可得完整模型。

深入浅出极大似然估计法

猜你喜欢