
一、前言
1、空间点集的最小包围球
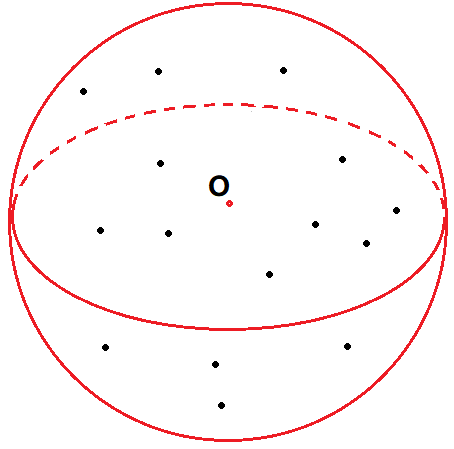
【例题1】三维空间中N(N <= 1000000)个点的集合,需要求一个球体包围所有的点,并且半径最小。算法要求给出这个球体的球心和半径大小。
图一-1-1
最小包围球在计算几何、碰撞检测、人工智能以及模式识别等领域都有着广泛应用。计算机图形学中,三维空间点集的最小包围球相比三维凸包而言,可以更加快速且精确的进行碰撞检测。而这些领域中点集的数据量往往是巨大的,所以快速有效的求解最小包围球的算法就显得尤为重要。
我们知道一个三维空间中离散点集的最小包围球一定是唯一的,只要求出这个球心,半径就是球心到所有点的距离的最大值,那么如何求出这个球心成了问题的关键。本文将利用随机增量算法从二维的情况(最小覆盖圆)对问题进行深入剖析,从而扩展到三维的情况。首先
来看下二维的情况:
2、平面点集的最小覆盖圆
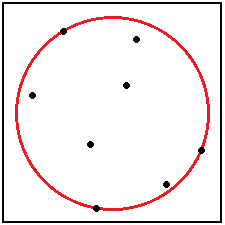
【例题2】平面上N(N <= 1000000)个点的集合,需要求一个圆,使得它能包含(覆盖)所有的点,并且半径最小。要求输出这个圆的坐标和半径大小。
图一-2-1
两者看起来是类似的问题,然而当我们思考空间问题没有头绪的时候,往往可以采用降维的思想,将空间问题转化成平面问题,然后再回到空间问题。那么,接下来本文将循序渐进,将求解最小覆盖圆的算法从O(n^4)优化到O(n^3)、再优化到O(n^2)。最后推翻之前的一切引入一个O(n)的算法。
介绍算法之前,首先来看一个概念,也是本文的核心算法,即随机增量算法。
二、随机增量算法
1、增量算法
增量算法(Incremental Algorithm)可以参考初中学的数学归纳法去理解。如果你已经熟悉动态规划,那么增量法就是动态规划的简化版。本质就是将问题划分为规模小一层的子问题,然后求解子问题后再计算原问题的解。
2、随机增量算法
随机增量算法的核心是一个洗牌算法,即随机打乱原本序列的顺序,如下:
void randomSuffle() {
for(i = 1 to n)
swap(p[i], p[random(1,n)]);
}
然后,按照洗牌后的顺序执行固定算法。由于洗牌是纯随机的,所以对于依赖于原序列顺序的算法来说,可以很好的规避掉"worst case"。并且可以通过随机性来计算概率和算法的期望复杂度。接下来就以最小覆盖圆来介绍随机增量算法的执行原理。
三、最小覆盖圆
1、O(n^4)算法
由于三个不共线的点确定一个圆,所以很容易想到一个O(n^4)的算法。
枚举任意三个不公线点算出对应三角形外接圆的圆心和半径,然后判断其它点是否在这个圆内。取所有满足条件的圆中半径最小的那个就是所求的最小包围圆。枚举三点复杂度O(n^3),加上一步判断轮询O(n),总的时间复杂度O(n^4)。
当然,这里漏掉了一种情况,就是有可能这个最小覆盖圆只经过两个点。所以还需要枚举任意两点为直径的圆,判断其它点是否在其内,这一步是O(n^3)的。所以总的算法复杂度还是O(n^4)。

图三-1-1
2、O(n^3)算法
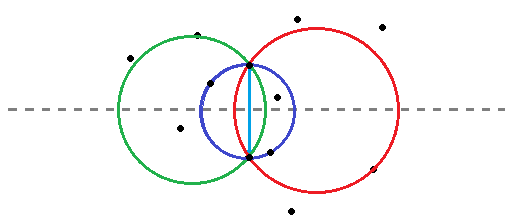
对以上思路进行一个优化,我们知道最小覆盖圆必然至少经过两个点(除非原点集一共只有一个点)。枚举任意两个点作为最小覆盖圆的一条弦,那么圆心必然在两点的中垂线上,如图三-2-1。这个覆盖圆有三种情况:
图三-2-1
a、圆心为这两点的中点(蓝色圆);
b、圆心落在弦的左边(绿色圆);
c、圆心落在弦的右边(红色圆);
图三-2-2
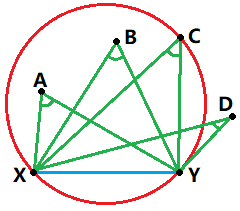
如图三-2-2所示,蓝色线段XY代表圆上的弦,其余的点和弦上两点XY构成夹角(如图中的∠XAY、∠XBY、∠XCY、∠XDY),夹角的关系为:圆外角<圆周角<圆内角,所以要覆盖所有的点,必然要让这个夹角最小。那么只要遍历所有的点,找出夹角最小的这个点,三点确定一个圆。然后再判断其余的点是否在这个找到的圆内,枚举任意一条弦的复杂度O(n^2),寻找夹角最小的点和判定是否在圆内是分开的操作,复杂度分别为O(n),所以总时间复杂度O(n^3)。
3、O(n)算法
最后介绍一个平均期望O(n)的算法。
1)随机增量法,打乱所有点的顺序。
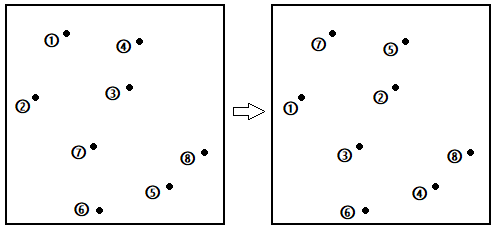
图三-3-1
2)以第①个点和第②个点为直径建立初始圆C,如图三-3-2所示。然后依次判断剩下n-2个点是否在这个圆内。
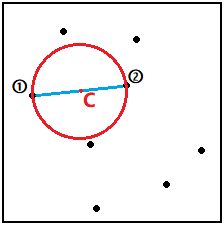
图三-3-2
如果点p[i]在圆C内(3<=i<=n),则不做任何处理;否则p[i]必定在前i个点所在最小覆盖圆的边界上,求出这个圆后更新C。于是问题转化成:求前i个点的最小覆盖圆,并且点p[i]在圆上。
3)以第①个点和第i个点p[i]为直径建立初始圆C'。然后依次判断前i个点是否在这个圆内。
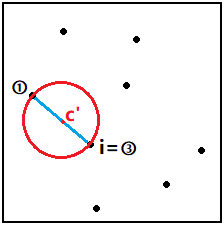
图三-3-3
如果点p[j]在圆C'内(j < i),则不做任何处理;否则p[j]必定在前j个点所在最小覆盖圆的边界上,求出这个圆后更新C'。于是问题转化成:求前j个点的最小覆盖圆,并且点p[i]和点p[j]都在圆上。
4)以第i个点和第j个点为直径建立初始圆C''。然后依次判断前j个点是否在这个圆内。
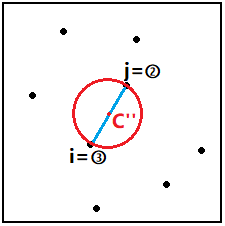
图三-3-4
如果点p[k]在圆C''内(k < j),则不做任何处理;否则用点p[i]、p[j]、p[k]三点确定一个圆更新C'',继续判断剩下的点l (k < l < j)。

图三-3-5
5)然后用C''更新C',再用C'更新C。就这样迭代求出包含前i个点的最小包围圆C。最后来看一下前5个点的最小覆盖圆。
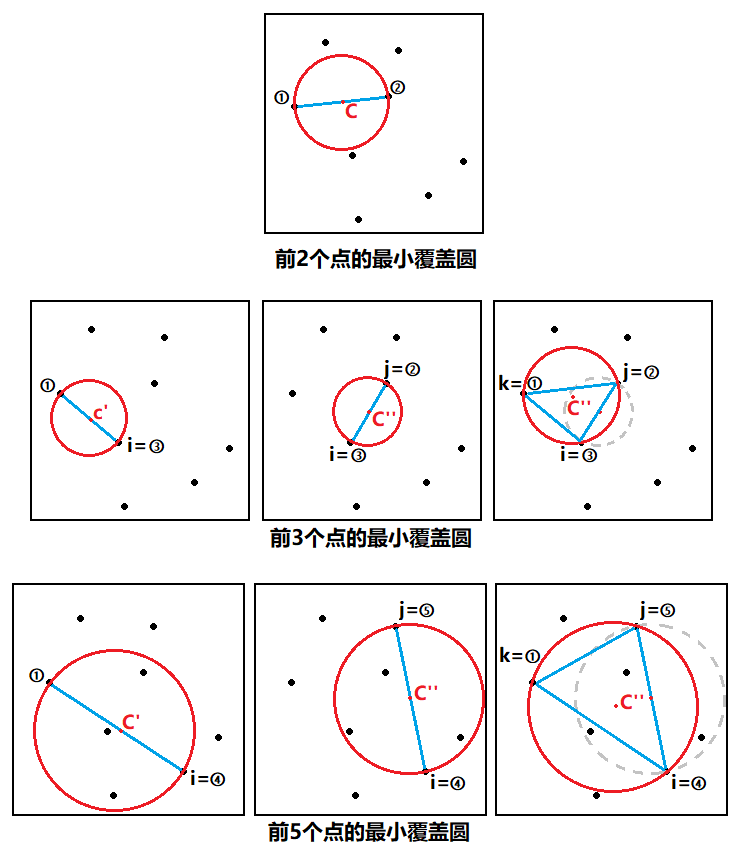
图三-3-6
可能这样讲下来有点迷,那么我们仔细分析一下上述算法。首先该问题有几个子问题,如图三-3-7所示,分别为:
【1】前i个点的最小覆盖圆;
【2】前i个点的最小覆盖圆,且点p[i]在该圆边界上;
【3】前j个点的最小覆盖圆,且点p[i]和点p[j]在该圆边界上;
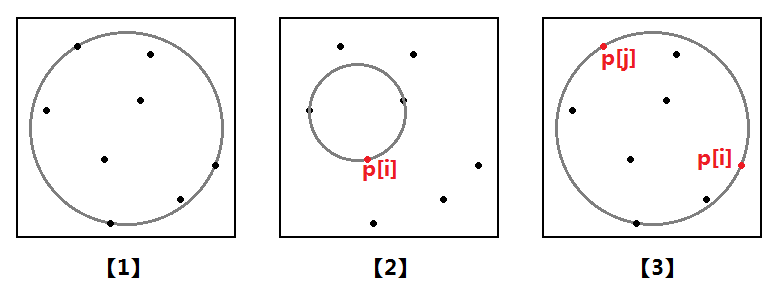
图三-3-7
这样把状态一划分,问题就变得简单许多了。自底向上的分析,【3】的情况我们已知圆上两点,那么只要再知道一个点就可以直接采用圆心(未知量)到圆边界点(已知量)距离相等列方程求解二元一次方程组计算得到(即三点确定一个圆),所以枚举所有前j个点计算半径最大的那个圆就是【3】问题的解。而【2】的情况是我们已知圆上一点,那么再枚举一点就可以转变成【3】的情况。同样,【1】的情况是只要枚举一点就可以转变成【2】的情况,自底向上的递归求解即可。
最小覆盖圆参考代码如下:
最小覆盖圆
4、O(n)算法时间复杂度分析
如果没有一开始的洗牌算法,考察该算法将会有三个for循环,那么最坏情况就是每次加入的点都在前i个点组成覆盖圆的外面,所以算法的最坏时间复杂度还是O(n^3)的。但是一旦顺序打乱以后,情况就不同了。
有一条很重要的性质就是:第i个点在前i-1个点所组成的最小覆盖圆外的概率为3/i。
证明如下:随机生成i个点,求出它们的最小覆盖圆,这个最小覆盖圆必然是圆上的某3个点确定的(2个点的情况计算得到的概率更小所以不考虑)。那么最后生成的那个点(第i个点)只要不是那3个点中其中一个,则必然落在圆内;反之在圆外。所以第i个点在前i-1个点组成的最小覆盖圆外侧的概率仅为3/i。
对于第i个点,只有3/i的概率是需要重新计算前i个点的最小覆盖圆,其它情况都是pass,所以总的均摊复杂度是O(n)的。
四、最小包围球
1、O(n)算法
最后我们将上述问题扩展为三维(如果对最小覆盖圆算法还没有完全理解请止步于此)。
算法思路完全参照二维求最小覆盖圆的情况:
1)随机增量法,打乱所有点的顺序。
2)【前i个点的最小包围球】以第①个点和第②个点为直径,两点中点为球心,建立初始球C。然后依次判断其它点是否在这个球体内,如果点p[i]在球C内(3<=i<=n),则不做任何处理;否则p[i]必定在前i个点所在最小包围球的边界上,求出这个球后更新C。于是问题转化成:求前i个点的最小包围球,并且点p[i]在球上。
3)【前i个点的最小包围球,且经过点 p[i]】以第①个点和第i个点p[i]为直径建立初始球C'。然后依次判断前i个点是否在这个球内。如果点p[j]在球C'内(j < i),则不做任何处理;否则p[j]必定在前j个点所在最小包围球的边界上,求出这个球后更新C'。于是问题转化成:求前j个点的最小包围球,并且点p[i]和点p[j]都在球上。
4)【前j个点的最小包围球,且经过点 p[i]和p[j]】以第①个点、第i个点p[i]、第j个点p[j]三点确定一个空间圆,以这个空间圆的圆心建立初始球C''。然后依次判断前j个点是否在这个球内。如果点p[k]在球C''内(k < j),则不做任何处理;否则p[k]必定在前k个点所在最小包围球的边界上,求出这个球后更新C''。于是问题转化成:求前k个点的最小包围球,并且点p[i]、点p[j]、点p[k]都在球上。
5)【前k个点的最小包围球,且经过点 p[i]、p[j]、p[k]】以点p[i]、点p[j]、点p[k]三点确定一个空间圆,以这个圆的圆心建立初始球C'''。然后依次判断前k个点是否在这个球内。如果点p[l]在球C'''内(l < k),则不做任何处理;否则p[i]、p[j]、p[k]、p[l]四点确定一个球,求出所有这些球中半径最大的更新C'''。最后用C'''更新C'',用C''更新C',再用C'更新C。得到前i个点的最小包围球。
虽然算法描述异常枯燥,但是2、3、4、5其实是类似的步骤,实际实现的时候还是很简单的。
最小包围圆参考代码如下:
最小包围球
最后讲一下第5步中三点确定球和四点确定球的计算方式。
2、空间三点外心
空间三点确定的最小包围球的球心一定是三点外接圆圆心(如图三-2-1中的O点,三角形ABC在球O的一个径面上),首先O在平面ABC上,所以我们先要求出平面ABC的表达式。
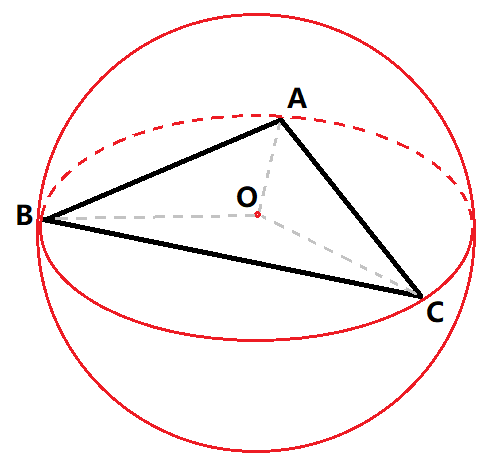
如图三-2-1
a) 点法式计算平面
平面方程用点法式表示为:
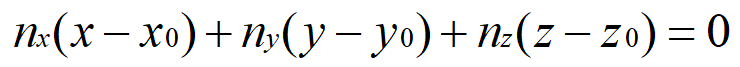
其中(nx,ny,nz)代表平面法向量,(x0,y0,z0)为平面上一点,那么现在就是要求平面法向量n,我们利用三维向量的叉乘来实现。
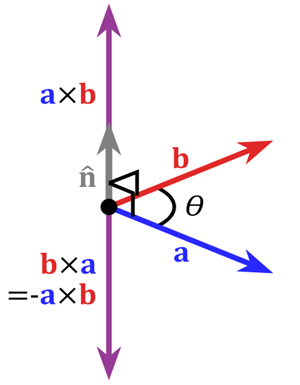
如图三-2-2
如图三-2-2,右手法则,四个手指按逆时针方向握紧(从a握到b),大拇指指向方向表示向量a和向量b所在的平面的法向量方向,即a×b。则有:
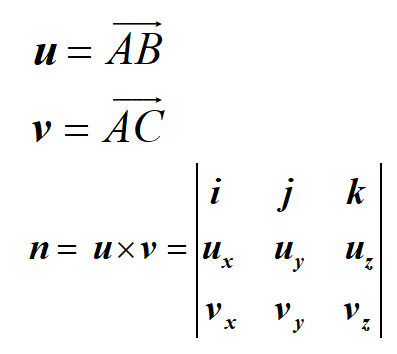
如图三-2-3
利用对角线法则,可得:
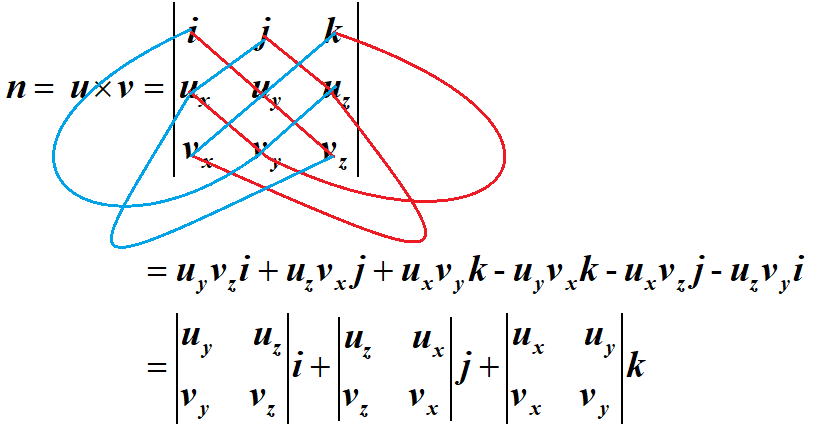
如图三-2-4
最后用A点(或B、C点皆可)替代(x0, y0, z0),代入点法式方程,就计算得出了平面ABC的一般式(A、B、C、D为常数):
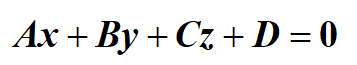
b) 距离法计算外心
令O为空间三角形ABC的外心,|OA|=|OB|=|OC|,拿|OA|=|OB|举例,有:
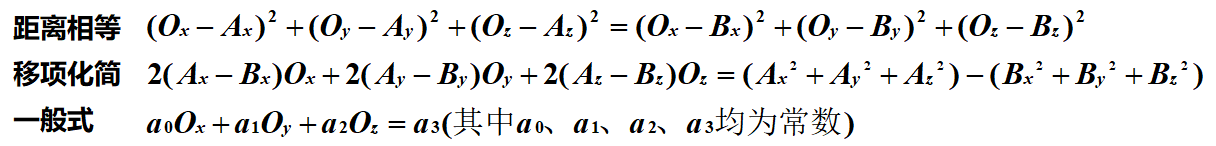
如图三-2-5

如图三-2-6
3、空间四点球心
首先,我们要排除任意三点共线和四点共面的情况,对于最小包围球求解过程中不会出现这样的情况(请读者自行思考)。所以我们只需要考虑四点不共面的情况。不共面的四点必然能够确定一个球,假设球心为O,则必然满足O到球面上的四点A、B、C、D距离相等。
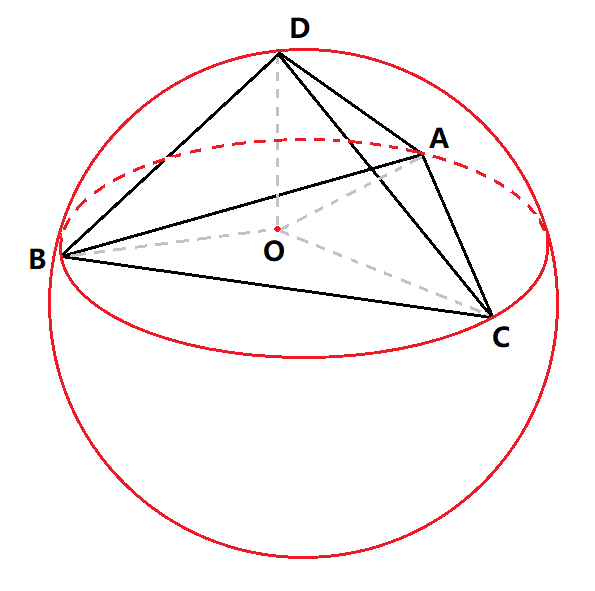
如图三-3-1
还是利用距离的两两相等,得到三个三元一次的方程,同样利用高斯消元求解(Ox,Oy,Oz)即可:
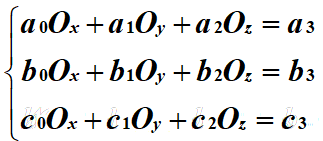
如图三-3-2
五、最小包围球相关题集整理
最小覆盖圆
最小包围球